ridix,

You might find the tips posted here...

Learning Advanced Tips and Techniques

...to be helpful (demonstrating how to preferentially manipulate the orientation of the rotate and protractor cursors.)

Taff

Also,...

...if you leave the 'Entity Info' box open while you work, you'll see that the area of selected face(s) is reported therein.

Thanks for the quick response. I'm left wondering whether a spring has both a stretch AND a compression character to it. (That's basically what Hooke's Law describes.) I haven't looked at the Newton specifics, but would be surprised if it didn't cover this.

I'll play with it some more, to see what a SketchyPhysics spring can do. Ideally, I'd like to be able to set the 'resting' length of a spring, then the 'stretch' (pull)resistance and the 'compression' (push)resistance. A real spring has these three defining characteristics.

If it won't work as described above, perhaps you can add the features to your notes, for possible future implementation. Thanks for your comments. I'll take a look at piston settings, as well.

[Taff]

Chris,

The textual description at the NewtonPlayground page, under "Springs," sounds about right - for extension, at least. There's no mention of compression characteristics, though. (It's basically the inverse, and it should be possible to implement it as such.)

Regarding your C++ question -- I stopped teaching myself new languages at Pascal and C. I'm an old-timer, and got tired of having to learn a new programming language every few years (Fortran, assembly, Basic, Pascal, C...) When C++ (Object-Oriented Programming) came out, I threw up my hands and gave up (although I'm currently considering the benefits of tackling java.)

I don't actually "know" that much about spring functions/calculations (but I know where to look in my library.) It's classical physics, so isn't as problematic as modern physics. I think the formulae for springs can probably be simplified to give a pretty good approximation of spring-function, without getting into calculus and differential equations. (Thank God!) Perhaps the Newton package already handles the implementations properly.

If a SketchyPhysics spring does not recoil (after stretching) or rebound (after compression,) thereby attempting to return to it's initial resting-state, then you're right that it wouldn't perform as 'true' spring would.

[Taff]

Chris,

You may find this enlightening (and there's C source code, too.) The discussion includes algorithms for gravitation, viscous drag, and Hooke's spring law:

Particle System Example

[Taff]

Bob,

I am, indeed, familiar with spring physics (see my full profile.)

What I'm asking is whether the SketchyPhysics spring algorithm is implemented such that a SketchyPhysics spring acts as would a real-world spring.

Your description should, however, help other readers who aren't that famililar with the subject. For future SketchyPhysics spring implementation, it should be noted that a spring may not have a compression characteristic, if the spring is fully compressed to begin with (think of a typical screen-door spring.) In such a case, the coils of the spring are initially in contact with each other, and can compress no further (referred to as "coil-bound.") It may be useful to be able to specify a zero compression factor in a future SketchyPhysics release. (Or am I missing something that can be done now?)

Offhand, I can't think of an example of the reverse, where an unrestrained spring has a compression factor, but no extension factor (i.e.; you can compress it, but can't stretch it.)

Ain't physics fun? It looks as though SketchyPhysics is introducing physics to users who would otherwise completely avoid the subject. From a former physics teacher,...

...thank you, Chris!

I'm curious whether SketchyPhysics springs can be used to demonstrate the equi-distribution "points on a sphere" physics problem.

Can a network (or mesh) of springs, which each stretch or compress relative to forces applied by other attached springs, fluctuate until forces are spread evenly (a state of equilibrium)?

Physics demonstrations that I've seen (implemented in java) writhe, gradually dampening in smaller-and-smaller increments, until equilibrium is reached (or a close approximation thereof.)

Has Sketchyphysics spring physics advanced to the point of being able to model such a thing in SketchUp?

For a java example of this (i.e.; Thomson's Problem,) see...

http://physics.syr.edu/thomson/thomsonapplet.htm

I wouldn't expect to model an entire sphere, with hundreds of points - a simplified spring-mesh of a portion of the surface would do nicely.

NOTES:
In my initial trials, it appears that each attachment point would need the rotational capabilities of a ball-joint.

Another example of a spring-mesh would be a trampoline membrane.

Apparently, a spring can pull (extension,) but can it push (compression)?

[ Taff }

My ancestry is Welsh (many generations ago,) so you're right.

'Taffy' is the anglicanized slang spelling of 'Dafydd' (Welsh for David.) 'Goch' is Welsh for 'red' (and, yes, I have red hair.)

Good catch, Bob

So, the 'perpendicular' thread WAS the one of which you were thinking. I still think it would be a nice feature if the 'circle' cursor could be dragged along an axis, similar to the 'protractor' and 'rotate' cursors. It sure would make drawing a surface perpendicular to a line (axis) a whole lot easier.

-Taff

Thanks, guys, I'll give it another try...

-Taff

Er, blubb,

You apparently need to be an approved beta-tester to use that download. The download will install the plugin, but won't initialize in SketchUp, unless you enter an approved ID (name) and key (password.)

I applied for beta-testing many weeks ago, but apparently wasn't approved, as I never received a response.

Bob,

Perhaps, the thread you recall was over at the Google Group:

http://groups.google.com/group/sketchupsuggestions/browse_thread/thread/71c9147152e1178d/4b96fa7fb78d4bfd

Even though the thread wanders off-track a bit, in the course of the discussion, Jean Lemire posted a model (to the 3D Warehouse,) demonstrating the 'follow me' tool technique, to which you refer:

http://sketchup.google.com/3dwarehouse/details?mid=b8182624bfbda7fd8c55d0fdf534ef19

From your description, the TubeAlongPath plugin appears similarly applicable to the technique.

__Olo,

One of the models here...
http://sketchup.google.com/3dwarehouse/cldetails?mid=2ff3fe050d0f83a549a70958796b8e8
...is a tutorial, regarding projecting, scaling and registering a texture image to align to a terrain surface. A few of the other models are examples where the technique was used.

Alan, I like your SWF idea, but I'm not keen to spend the amount of money being asked for Dreamweaver and other SWF editors I've found through web searches.

Can anyone suggest an alternative that they've actually used, and found to be capable and reliable.

I'm currently stuck with the old standby - animated GIFs.

Taff

SketchUp is fully capable of doing so. (Wrong term though -- SketchUp uses 'drape' to describe something else. If you're searching the Users Guide, you don't want to search on that term.)

You want to 'project' a texture onto the terrain surface. This is described in one of the Google video tutorials here:
http://sketchup.google.com/gsu5vtvideos.html
(#12, "Using images as signs")

I've produced several textured terrains with projection, including a tutorial:
http://sketchup.google.com/3dwarehouse/cldetails?mid=2ff3fe050d0f83a549a70958796b8e8&num=50&scoring=d

Hopefully, one of these models provides the help you need.

Regards,
Taff

wyteshooze,

Actually, I can provide a a more-encompassing 3D Warehouse URL than the one Fred graciously mentioned. In this collection, you'll find Help-Group-discussion models from many contributors. Several of the models are tutorials addressing spiral/helical construction methods, including ramps and stairs:

http://sketchup.google.com/3dwarehouse/cldetails?mid=34d9da9dcbd66dc16aa25eeaaa5db894&num=50&scoring=d

(white shoes?)

Regards,
Taff

Tom,

I don't know if this is the tutorial, of which Paul was thinking...

Error 404 (Not Found)!!1

(sketchup.google.com)

...but perhaps it will help, regardless.

The technique makes use of 'projected' texture, as described in the Google video tutorial #12, "Using images as signs," available here:

Error 404 (Not Found)!!1

(sketchup.google.com)

Paul's reference, "...apply the color image to the flat view," is evident in both tutorials, and is the single textured plane where texture sizing, scaling, rotation and orientation is adjusted.

The texture is set (using the context menu) to be 'projected.' Then the eyedropper tool can be used to sample the 'flat' image, and the paintbucket used to apply (project) the texture image onto the undulating surface aligned underneath (make sure it's not a group, or enter/edit the group before painting.)

If, after reviewing the video and tutorial, it still doesn't make sense, let me know.

Regards,
Taff

Pilou,

TopMod looks fun - and it's free? So, what's the catch?

I see that it's from the university, Texas A&M. Perhaps free distribution simply increases the exposure and reputation of the university's computer-visualization program, thereby ensuring greater student enrollment.

In your opinion, how good is the program?

Taff

caddict,

Using 1000 edges for the circles provides pretty good precision. If you go into 'Model Info > units' and change the precision to it's maximum (or is it 'minimum',) the 'entity info' box shows that the rotation has reduced the hexagon edges from 1000mm, to 999.997867mm.

Certainly, in real world construction, 0.002mm precision is more-than-acceptable. It's highly unlikely that this degree of precision would ever be necessary or practical.

But for mathematically-obsessive personalities, like me, I still want to know why SketchUp doesn't provide the capability to rotate/intersect precisely. Computationally, it's possible - but SketchUp doesn't implement such an inference.

Regarding your method, if you use the 'Model info > units' settings to set an even higher precision, and you play with the 'snapping' setting, I suspect you can achieve even greater accuracy.

Since the entire circle is not needed, you could draw just the arc portion of necessity. If you set the arc segments to 1000, as you did for the circle, you might approach an exact 1000mm hexagonal edge.

Another trick is to scale the entire model up, perform the rotations, then scale back down. Since SketchUp is sensitive to small dimensions, and can thereby 'choke' on certain operations, the up-scaling circumvents the problem. You could scale up by a 100x-1000x multiplier, if necessary.

If you're trying to produce a soccer ball, this degree of precision borders on ridiculous. But what if you're trying to model a soccer ball for nanobots to play with...?

Regards,
Taff

caddict,

I had SO many problems with the same thing last year. There was a discussion on one of the Google groups regarding the truncated icosahedron, face-rotations and intersection accuracy. This generated a lot of experimenting with face rotations, and several new discussions.

Everyone agreed that SketchUp could use some kind of enhancement to the rotation tool that would allow inferencing to a precise intersection point on a line. Who knows if we'll ever see it. The concensus was that everyone would love to be able to rotate two faces up to their intersection point (line, actually.)

I'm afraid that I sorta 'killed' the discussion about the truncated icosahedron (the original topic) with an historical construction method: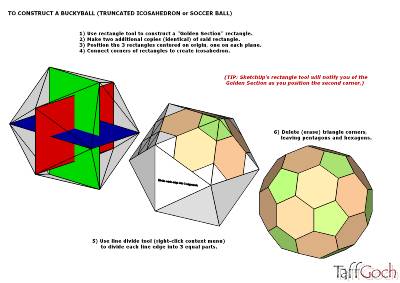http://sketchup.google.com/3dwarehouse/details?mid=3af9af9384d2097858f8f3aa29de1c06

However, the rotation issue still hasn't revealed any 'eureka' moments, where someone has provided a workaround. It's been discussed before, but maybe this time someone with a fresh perspective will surprise us all. (I've got my fingers crossed...)

Regards,
Taff

Experimenting,...

...I find that, if you change the view to 'hidden line' mode, instead of 'monochrome,' then shading is not applied. Also, if shadows are turned on, all shadows become a single dark color, rather than a gradient.

Taff