Version 4.4.0 - 03.12.2026
- Enabled the following method within the Medeek Wall API: wall_draw
- Added the Medeek Wall API Documentation page to the website.
Version 4.4.0 - 03.12.2026
Version 2.1.2 - 03.07.2026


For this detailed breakdown you need to have the "separate callouts" and "weight callouts" both enabled.
Version 2.1.1 - 03.06.2026
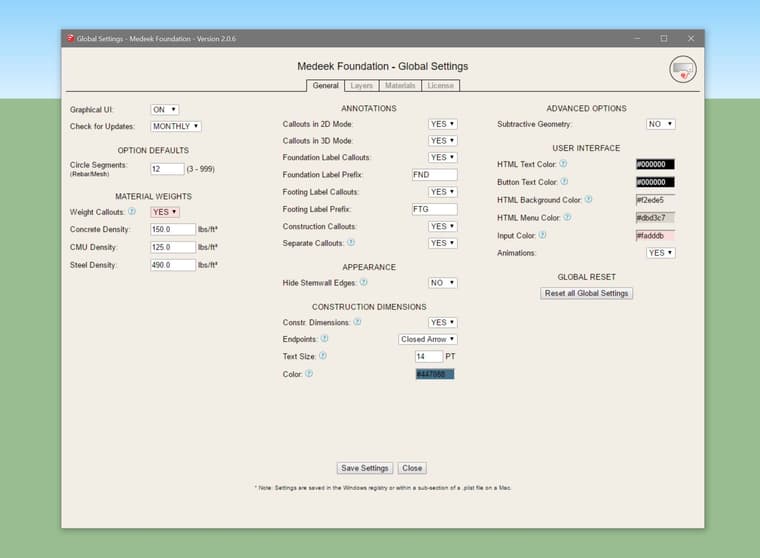
This update per customer request.
The density of the concrete, CMU and steel can all be customized in the global settings as shown in the image above. I will probably enable this feature for other foundation assemblies if it is requested.
Version 2.1.0 - 03.05.2026
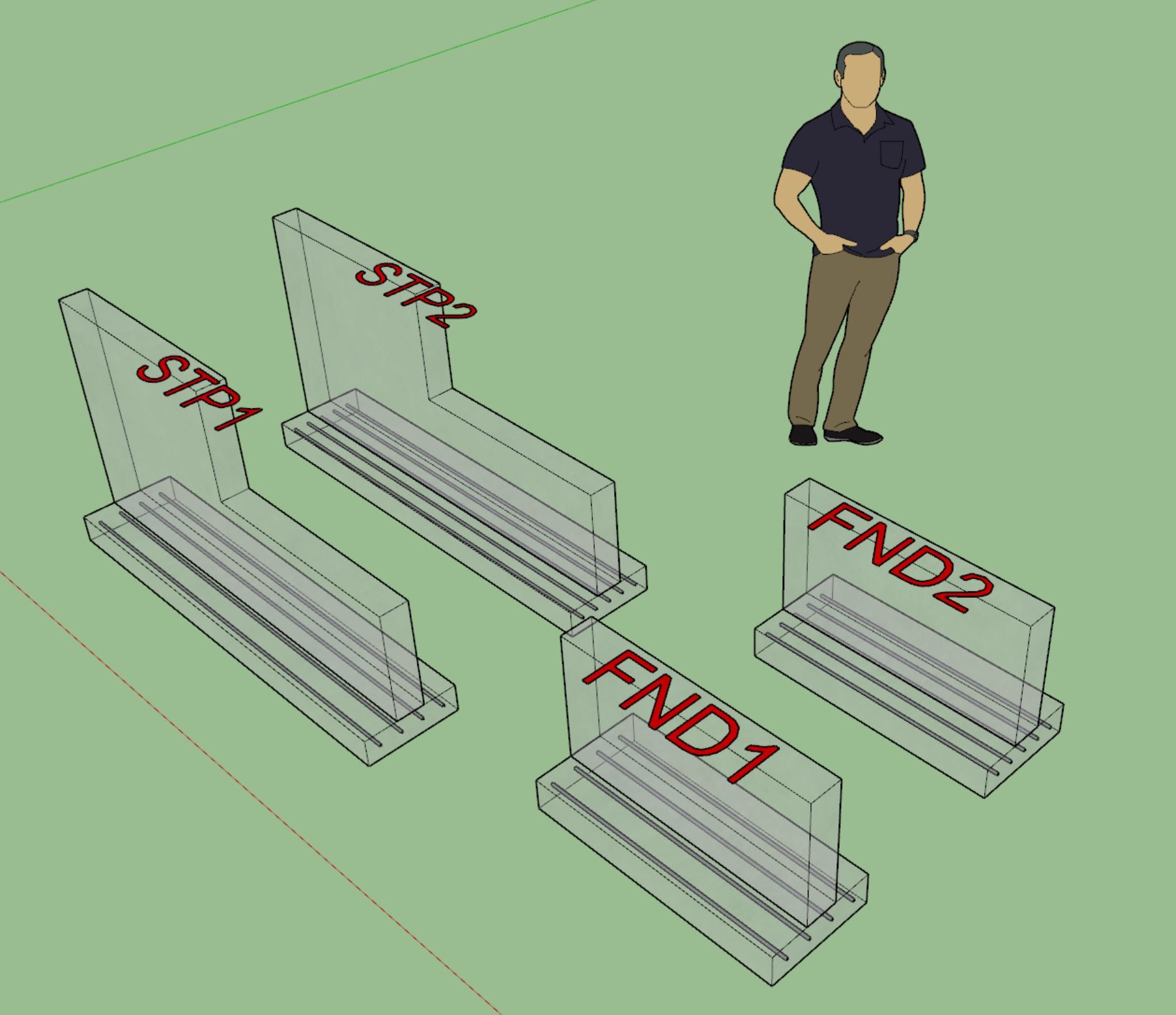
This update per customer request.
I did not update the legacy stemwall tool since I will be retiring that tool eventually but I have not decided on a date just yet.
I would highly recommend that new users of my extensions watch this intro video as well as those who are contemplating purchasing any of the extensions.
Version 2.0.9 - 03.03.2026

This update per customer request.
Version 2.0.8b - 03.02.2026
Version 1.1.9 - 03.01.2026
Version 2.0.8 - 03.01.2026
This update per customer request.
Version 4.3.8 - 03.01.2026
Version 4.3.7 - 02.28.2026
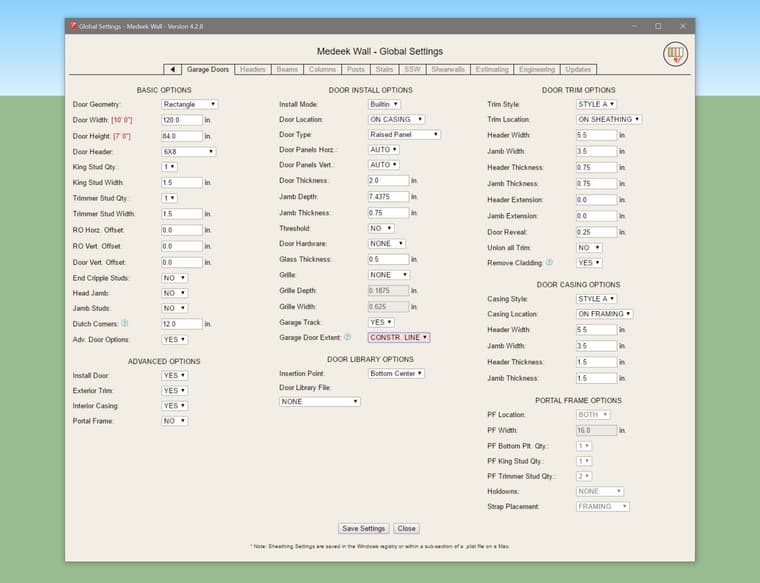

This update per customer request.
I've recently had the request to add an annotation to the wall panels that displays the cladding area (net and/or total). See example below:
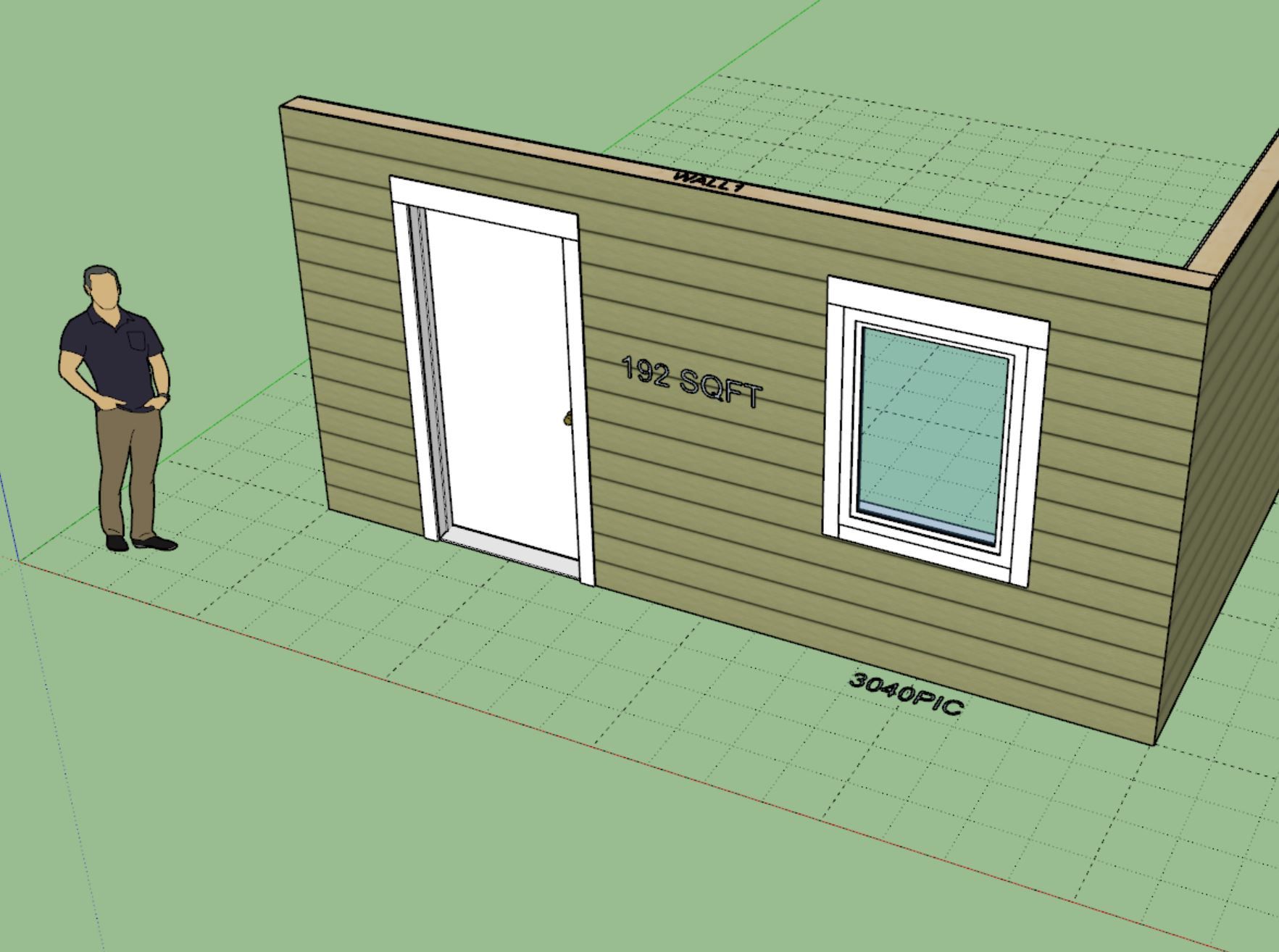
Obviously I would add this to a separate dimension layer/tag so one could easily toggle it on and off. One can already get this information from the estimating module but this would simply provide a quick and easy way to pull the sqft (area) of a wall panel. By default this extra annotation would be turned off but if desired one could enable it in the global settings (Sheathing tab).
It would not be too much trouble to add something like this in but I just want to roll this in front of a larger audience and see if it is even something that would be useful or beneficial to the majority of the user base.
Version 1.1.8 - 02.26.2026
I think that gets us to nine different I-Joist manufacturers in the US and Canada. I think Lebel and Eacom (both out of Canada) also make some I-Joist products, but I don't believe they have as much market share as the companies listed below:

 Joists
Joists I-Joists
I-Joists I-Joists
I-Joists I-Joists
I-Joists I-Joists
I-Joists I-Joists
I-JoistsVersion 1.1.7b - 02.25.2026
Previously if you set the ceiling inset parameter to zero the logic would try to apply this zero offset and would throw an error and then abort the draw process. I guess I automatically assumed a non-zero inset (ie. 3.5 or 5.5 inches) and did not test it with a zero inset, so I never caught this specific state.
Shout out to @ArtisanTony for finding this one for me. I probably would never have found out since I'm always using an inset when I turn on the gypsum, I don't think I've ever used a zero inset.
Keep sending in those bug reports, it is greatly appreciated. This extension isn't very old so I know there are still a few more small fires to put out, the trick of course is finding them all.
Version 1.1.7 - 02.25.2026

Added per customer request.
Version 1.1.6 - 02.24.2026
Added per customer request.
Version 1.1.5 - 02.23.2026
 I-Joists: RFPI 20, RFPI 400, RFPI 40, RFPI 70, RFPI 90, RFPI 40S, RFPI 60S, RFPI 80S.
I-Joists: RFPI 20, RFPI 400, RFPI 40, RFPI 70, RFPI 90, RFPI 40S, RFPI 60S, RFPI 80S.
The Roseburg I-Joists include LVL and solid sawn flanges. This manufacturer of I-Joists added per customer request.
Version 1.5.8 - 02.16.2026
Version 4.3.5 - 02.15.2026
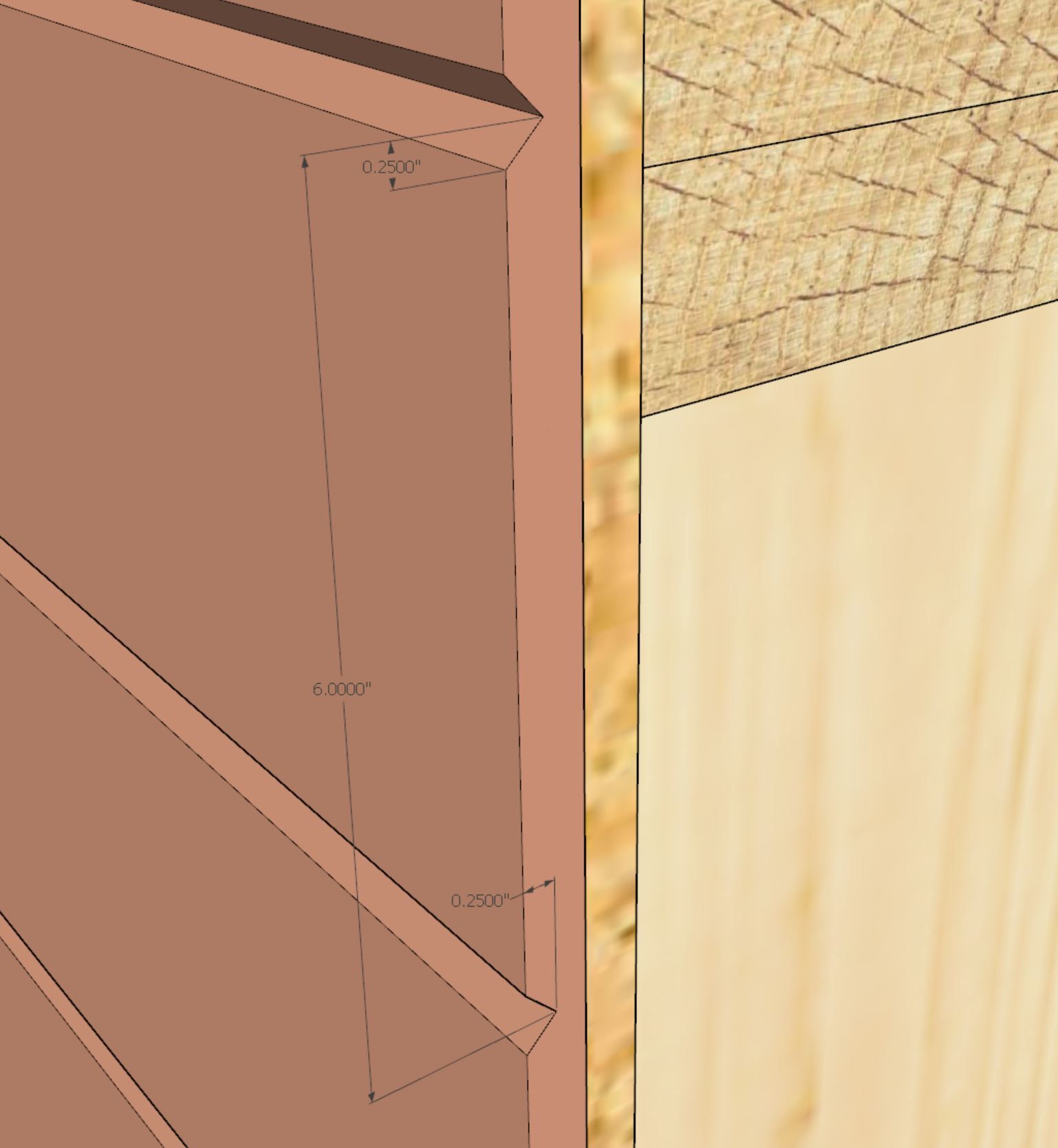
This 3D material by customer request.
The three numeric parameters in order are: board spacing, bevel height and bevel depth
An example of this 3D material might be: beveltg_6.0_0.25_0.25