Mini-challenge
-
@andybot said:
@mac1 said:
[attachment=1:3b4i0fcr]<!-- ia1 -->mini__mac2.skp<!-- ia1 -->[/attachment:3b4i0fcr]Here is improved on solution I posted early and all dimension have been verified to SU 32 bit float accuracy against the close form solution I presented above.
Note I have been using some of the post dimension Jeff posted early of 96" post height, 65" spacing and 3.5 rail width.
No plugin is used.
I did use the technique I posted almost a year or so ago on the exact solution of sphere line intersection.Hey Mac1 - what "sphere" are you using? It's not clear in your model what your steps are.
Sorry did not make my self clear enough for you. At the bottom right I show the intersect point, at the bottom left I show the center of the sphere. Since SU is a 3d program any time you talk about intersecting a rotated line with a target line it must be on a spherical basis. There was no intent to show a sphere but the math basis must consider that or you do not have a closed form solution. SO the directed line segment from the line rotation point ( aka center of sphere) to the intersection of the target line( used as ref for guide point) is the points one needs to get the angle of rotation and the intersect with the rail width to the left post. SO the intersect ( guide point ) at the target line, the two 3.5 inch spaced guide lines are all rotated to the top of the left post to establish the points needed to draw the 3.5 rail to the proper points. Here is a screen shot of the skip file I posted some time ago.
[attachment=0:3b4i0fcr]<!-- ia0 -->SPHERE LINE INTERSECT.jpg<!-- ia0 -->[/attachment:3b4i0fcr]
-
BTW you need ground truth to know if your model is correct.
I presented the closed form solution for the 2d case above. Here is the excel results to check my model' -
The fact that this thread is already 19 pages long has made me seriously consider learning either MoI or Rhino.
-
@mac1 said:
BTW you need ground truth to know if your model is correct.
Clear as mud
You still don't show your steps. I'd love to see the "sphere" you are using, or are you just talking about calculating and not modeling. Sure, anyone understanding basic trig can calculate the length of the edge based on the diagonal, that's been done a few times in this thread, but entering numbers seems to still end up with rounding errors in SU...
-
Take Moi : It's the SU of Nurbs against Rhino !
Less powerful functions but it's not the same spirite!
I don't abort to find a more easy answer at this damned problem of align rotation who fail at mini micro sub-atomic snaping!
-
Greetings all,
A few months back I had a similar conundrum..........after fussing a bit I just "eyeballed it" to get my cross bracing.
"Knowing" the challenge, I have taken another swing at it...........though it still does not "zero out".
In short.........center the cross brace and scale it's "ends" to meet the vertical(s).
Sorry..........I do not possess video skills.
Best,
-
@andybot said:
@mac1 said:
BTW you need ground truth to know if your model is correct.
Clear as mud
You still don't show your steps. I'd love to see the "sphere" you are using, or are you just talking about calculating and not modeling. Sure, anyone understanding basic trig can calculate the length of the edge based on the diagonal, that's been done a few times in this thread, but entering numbers seems to still end up with rounding errors in SU...
I guess the best I can suggest is to use your imagination. I am sure you understand a line rotated around a point through 4 PI steradians makes a sphere. Since this is really 2 d problem the sphere degenerates to a circle. I did not calculate the lengths nor rotation and have not seen anyone present a closed form solution to that.I have seen some claims but will re-look since you assert they did post. I presented a closed form solution and since edges,angles and intersect points are not known math solution is not what you assert. The ground truth which was calculated was only done to validate the model approach. That means any different answer is either a model error or a SU limitation. The model results I presented are validated by the ground truth( calculated) ( With in of course SUs 32 bit float or really 24 bits( 1 bit for sign and 8 for exponent are used leaving 23 but using the sign bit makes 24 bits or 7 digits.) Accuracy for the rotation angle ,because of how SU truncates the number of digits reported, I did not validate.
All the info you need has been presented. I suggest you look at all my post just not the last one.The key to the model is finding the intersect point shown which was a subject of my post maybe 2 years ago. The approach is shown in the jpg posted above.
You are allowing yourself to get stove piped by looking for a sphere.
The steps are finding an intersect point and one rotation as shown. -
.
is there a way you can dumb it down for us plebs?
i've never even heard the word steradian before (and if i have, it definitely never stuck )i can't tell if you're showing a solution or.. what..
-
@unknownuser said:
Take Moi : It's the SU of Nurbs against Rhino !
Less powerful functions but it's not the same spirite!Moi also makes it easier to stay in perspective viewport.. it has really nice inferencing and navigation..
michael just hooked up copy/paste between moi&rhino on mac so i think i'll be spending more of my time in moi now and just pasting into rhino if i need something more robust for a particular scenario..@unknownuser said:
I don't abort to find a more easy answer at this damned problem of align rotation who fail at mini micro sub-atomic snaping!
lol.. i've tried so many things over the past few days to no avail.. i think i'm done trying..
i'll just wait a year or two when this thread is randomly rejuvenated with someone showing an incredibly simple way of doing this
-
@unknownuser said:
.
is there a way you can dumb it down for us plebs?
i've never even heard the word steradian before (and if i have, it definitely never stuck )The surface area divided by the square of the radius yields a solid angle subtended by the surface area in square radians(steradians)
i can't tell if you're showing a solution or.. what..
Yes but not for the challenge.
This is the same approach you looked at early in the postings but with improved accuracy.
Today is the first time I read all post because I did not want others good ideas to creep into my thought process. To refresh: It is simply a rotation of a guide point form the post down to two parallel 3.5" separated guide lines ,with the correct intersection this time=>Based on a post I did ,several years ago before any plugin, on sphere line intersect. That guide point and guide lines are then rotated back to the post to establish the geo. I have an old simple excel spread sheet that gives the exact x,y,z coordinates for that guide point=> even for spherical case. -
@mac1 said:
This is the same approach you looked at early in the postings but with improved accuracy.
I was pretty sure you were not showing anything new. So yes, you are relying on calculation, just like Jeff was relying on the DC to caculate the position of the long edge. This, as far as I can tell, does not solve the challenge in that there is no use of SU inference or snapping to achieve what SU would consider a coincident point. So far as I can tell, Gilles is the only native SU method, and TIG and Fredo both have plugin solutions. (true tangents, and updated protractor, respectively)
Thanks Jeff for this interesting challenge, hope you find another new mindbender ( but not too soon
)Andy
-
Very accurate but...not the perfection!
No problem of thickness measures as the block is rotating
-
Here's another variant... OK, it's NOT 100% accurate... but near enough... AND the rail's cross-section is exact, with only the length slightly off ~0.02mm...
-
has anyone tried these solutions that are so so close by modeling them 10x or 100x their scale? will sketchup perform that angle alignment better when the distance between the 2 points is greater? is this a case of sketchup not real great at really really small geometry?
-
@bmike said:
has anyone tried these solutions that are so so close by modeling them 10x or 100x their scale? will sketchup perform that angle alignment better when the distance between the 2 points is greater? is this a case of sketchup not real great at really really small geometry?
If you use my latest method after you scale x100, then scale down x0.01 the length 'error' is x10 less - ~0.002mm rather than ~0.02mm - an improvement but not that significant as it was already negligible !
-
@tig said:
@bmike said:
has anyone tried these solutions that are so so close by modeling them 10x or 100x their scale? will sketchup perform that angle alignment better when the distance between the 2 points is greater? is this a case of sketchup not real great at really really small geometry?
If you use my latest method after you scale x100, then scale down x0.01 the length 'error' is x10 less - ~0.002mm rather than ~0.02mm - an improvement but not that significant as it was already negligible !
so its not a problem of sketch up working really small or really large (like other things) - but just a general inability to snap / reference correctly? is that the consensus?
-
Also SketchUp merges very close endpoints.
-
Hi again,
I did not read all the posts, but here would be my 'manual' method with just SU tools.
This is derived from the mathematical solution, but for the geometric construction, the caveat is that circles in Sketchup are made of segments, so that their intersection is never perfectly accurate. So, I use here circles with 256 segments which seems good enough.
The method just helps drawing the guide for teh rotation. So it is independent of the shape of the board.
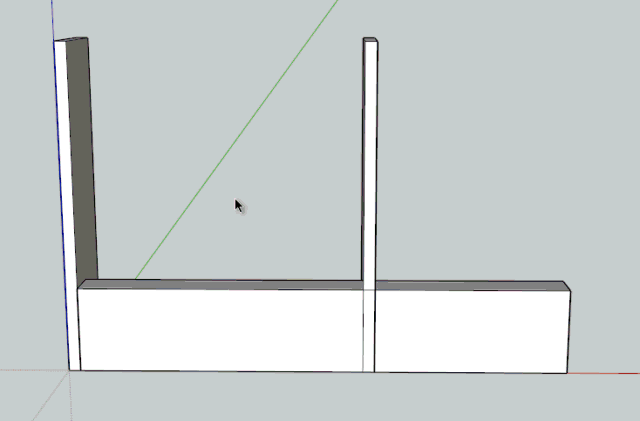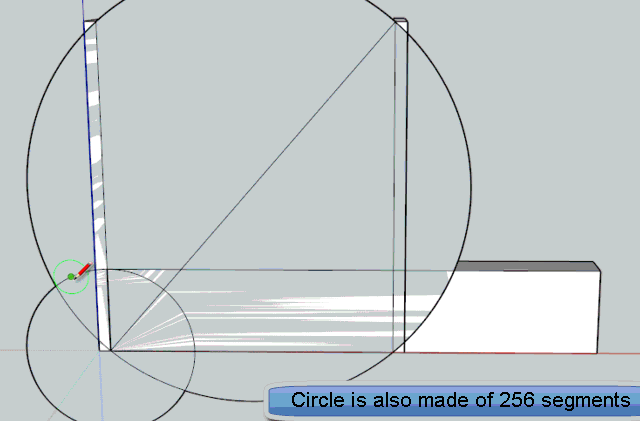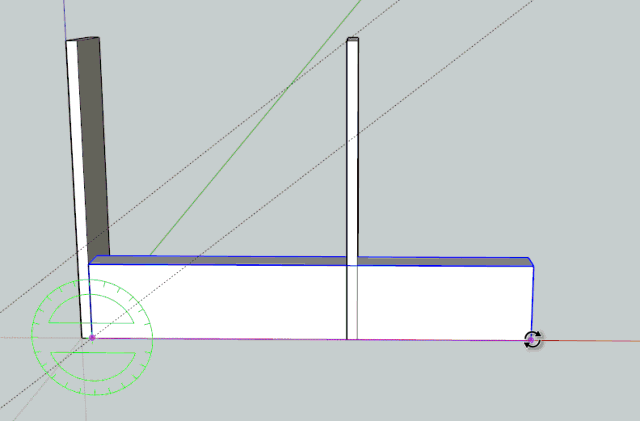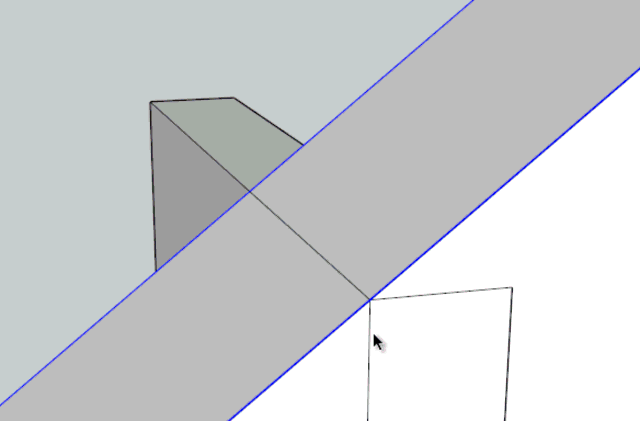
Fredo
PS: the offset angle is equal to arc sinus (width of board / length of diagonal)
-
@bmike said:
so its not a problem of sketch up working really small or really large (like other things) - but just a general inability to snap / reference correctly? is that the consensus?
the problem isn't about scale.. and not necessarily about poor snapping ability (in general) as sketchup's inferencing is actually very good.. only when rotating does this problem rear it's ugly head..
here's an example which shows the problem more effectively..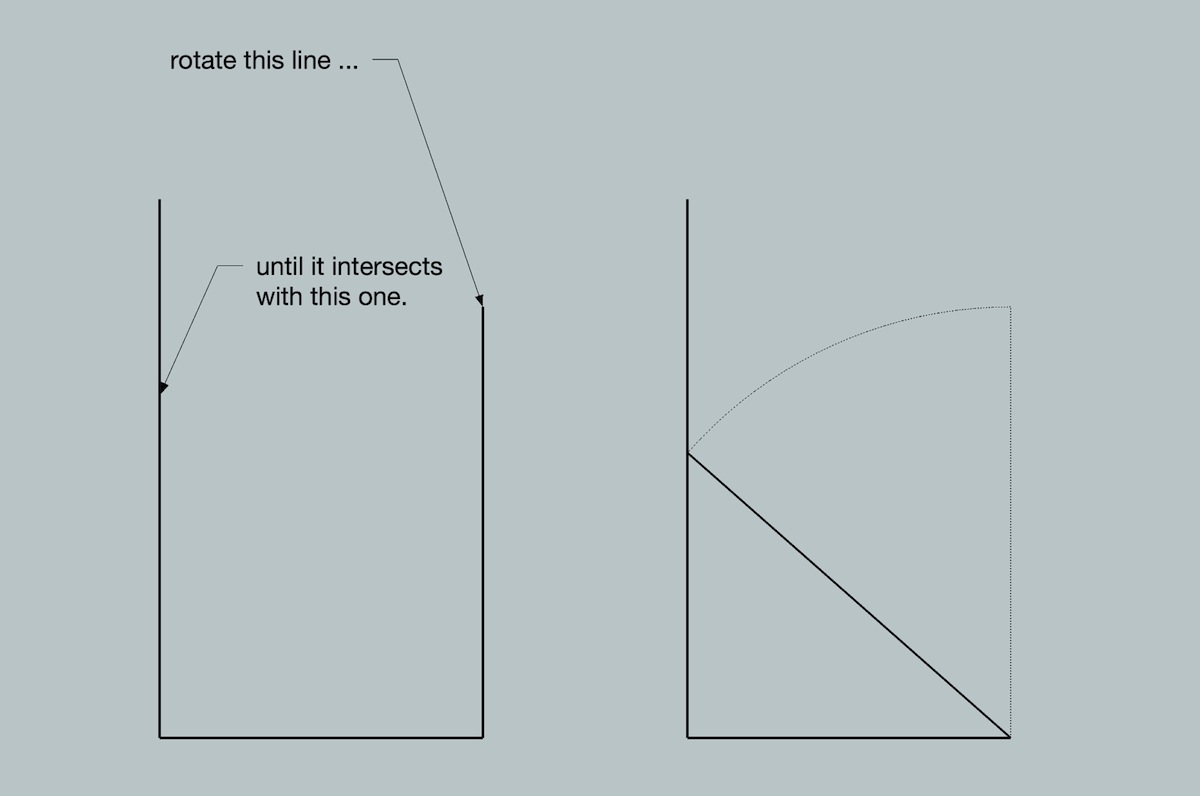
if you try this scenario, you'll see sketchup basically ignores the vertical line that you need to snap to..
[edit].. and in this circumstance, there are a couple of workarounds.. some of which are being shown in this thread.. there's the brute force method in which you draw an arc with a very high amount of segments in order to obtain an intersect point.. you could use TIG's true tangents to obtain a snap point.. you could use a calculator (or DC) to find a rotation angle or height along the vertical line to snap to..
the challenge, in this scenario, is to find a geometrical relationship which would allow you to use only sketchup tools to obtain an absolute snap.. if you could figure that out, then it could (probably) also be applied to the original scenario in this thread. (and actually, it doesn't have to be sketchup tools.. more like -- if you can find a geometrical relationship which doesn't involve using a compass, then there will be a way to draw this accurately in sketchup)
-
Advertisement