Line length on circle scaled to ellipse is very wrong
-
Pilou. The actual line length is 2155 +/- 5. measured in the real world.
This thread is starting to make my brain hurt...so, respected elders, is it a Bug or not?
-
@unknownuser said:
Using Approximation 2, the perimeter would be 2118.265712279433
A nurbs program 400 * 900 ellipse gives 2118,2799332 length line perimeter
Sketchup gives 2118,276442 with circle 1000 segments
-
I think it is a bug. I looked up the formula for perimeter of an ellipse and compared that with what SketchUp's entity info returns. For a 10x20 ellipse, the result should be 96.88. SketchUp variously returned 62.83 (20*pi), 111.3, and 113.27.
-
There was already a bug submitted for this, yes it is a bug. Also changing lengths when copying an ellipse is a bug. They are in the database and most likely sometime in the near future will be fixed.
-
There is no closed form equation for perimeter of ellipse
it is approximated by p=2PIsqrt[[[ a^2+b^2]/2]^1/2]
The correct value p=4aE where E is the elliptic integral where k=1/asqrt[a^2-b^2] -
@mac1 said:
There is no closed form equation for perimeter of ellipse
it is approximated by p=2PIsqrt[[[ a^2+b^2]/2]^1/2]
The correct value p=4aE where E is the elliptic integral where k=1/asqrt[a^2-b^2]Yeah, what Mac said...
-
Mac is right, though there are several other approximate formulas that are better than the one he gave. Also, there are power-series that can be run to enough terms to get arbitrarily close. The point here is that even the sum of the lengths of the edges in the oval comes much closer than the strange values that SketchUp sometimes provides.i
-
The best estimation of the circumference I've found is this:
def self.circumference(major, minor) a = major / 2.0 b = minor / 2.0 d = b / a x0 = d**0.5 x1 = d x2 = d**1.5 x3 = d**2 x4 = d**2.5 s0 = 3929 * x0 + 1639157 * x1 + 19407215 * x2 + 24302653 * x3 + 12892432 * x4 s1 = 86251 + 1924742 * x0 + 6612384 * x1 + 7291509 * x2 + 6436977 * x3 + 3158719 * x4 c = 4 * a + b * (s0 / s1) return c endIt's extremely accurate, unfortunately I don't know where I found it so I can't give credits.
-
And what is its result in this case ? (Ellipse 400*900)
-
@pilou said:
And what is its result in this case ? (Ellipse 400*900)
2118.2799288074484
The result above is for major = 900, minor = 400, if your input refers to the semi axes multiply the result by 2.
-
@ Caul
So my result of Nurbs prog was not so bad!
2118,2799 332 against your theoric 2118.2799 288074484Sketchup gives 2118,27 6442 with circle 1000 segments!

But what think of this
@unknownuser said:
The actual line length is 2155 +/- 5. measured in the real world.
Measured with ?

or

or...? -
Attched is pic of ellipse drawn by the means of supplemental chords with no scaling. I included different seg counts just to show what can be done. If there is intersest I'll redo with more care.
Su reports length of 48.364" for size shown.
If you can run the polynomial curve fit equation shown I would appreciate. If this approach is useful for you I'll redo and show how to draw. It is a little more complicated than scaling but not much since you can draw 1/4 and then mirrow.
Oops see one dimension got cropped it is 10"
-
@pilou said:
@ Caul
So my result of Nurbs prog was not so bad!
2118,2799 332 against your theoric 2118.2799 288074484Sketchup gives 2118,27 6442 with circle 1000 segments!

But what think of this
The actual line length is 2155 +/- 5. measured in the real world.Measured with ?
A piece of string Pilou, sorry I cant recheck it, the job is done and dusted.
-
@mac1 said:
Attched is pic of ellipse drawn by the means of supplemental chords with no scaling. I included different seg counts just to show what can be done. If there is interest I'll redo with more care.
Su reports length of 48.364" for size shown. (1228.4456mm)
If you can run the polynomial curve fit equation shown I would appreciate. If this approach is useful for you I'll redo and show how to draw. It is a little more complicated than scaling but not much since you can draw 1/4 and then mirrow.
Oops see one dimension got cropped it is 10"[attachment=0:cf3intzr]<!-- ia0 -->conjuate ellipse.jpg<!-- ia0 -->[/attachment:cf3intzr]Curious to see how you do it Mac. (Tho' the curve on the minor axis is a bit pointy n'est pas?)
-
The code below constructs an ellipse in a group centered at origo where all edges have the exact same length. Since the script only computes a quarter ellipse the final full ellipse has an edge count divisible by 4. There's a "user interface" at the end to set major, minor and edge count. The circumference converges to the correct value with increased edgecount.
To run it, just paste the code into the ruby console and press enter.
module CAUL_RegularEllipse #hack found on the internets. Very accurate... def self.circumference(major, minor) a = major / 2.0 b = minor / 2.0 d = b / a x0 = d**0.5 x1 = d x2 = d**1.5 x3 = d**2 x4 = d**2.5 s0 = 3929 * x0 + 1639157 * x1 + 19407215 * x2 + 24302653 * x3 + 12892432 * x4 s1 = 86251 + 1924742 * x0 + 6612384 * x1 + 7291509 * x2 + 6436977 * x3 + 3158719 * x4 c = 4 * a + b * (s0 / s1) return c end #find the intersection between a positive half ellipse at (0, 0) and a #positive half circle at (h, k) with radius r in the first quadrant. def self.circle_ellipse_intersect(a, b, h, k, r, c) #start point must be chosen with care so we don't end up outside the domain x = h - c * r epsilon = 0.000000000000001 f_e = f_c = 0 (0..15).each { |i| f_e_sqr = 4 * (a*a * b*b) * (a*a - x*x) f_c_sqr = 2 * h * x + r*r - x*x - h*h df_e_sqr = a*a * b*b * (a*a - x*x) df_c_sqr = r*r + 2 * h * x - x*x - h*h return nil if f_e_sqr < 0 || f_c_sqr < 0 || df_e_sqr < 0 || df_c_sqr < 0 f_e = Math;;sqrt(f_e_sqr) / (2 * a*a) f_c = Math;;sqrt(f_c_sqr) + k df_e = -(b*b * x) / Math;;sqrt(df_e_sqr) df_c = (h - x) / Math;;sqrt(df_c_sqr) break if (f_e - f_c).abs <= epsilon x = x - (f_e - f_c) / (df_e - df_c) } return [x, f_e] end #given a positive x-value, return the point on the ellipse in the first qudrant def self.get_ellipse_point(major, minor, x) a = major / 2.0 b = minor / 2.0 f_e_sqr = 4 * (a*a * b*b) * (a*a - x*x) f_e = Math;;sqrt(f_e_sqr) / (2 * a*a) return Geom;;Point3d.new(x, f_e, 0) end #return how close the ellipse gets to the endpoint at ex with #bits segments #of length len. def self.test_ellipse(len, q_bits, major, minor, ex) a = major / 2.0; b = minor / 2.0; d = count = 0 coff = [0.99999999, 0.00000001, 0.5] p0 = Geom;;Point3d.new(a, 0, 0) pe = get_ellipse_point(major, minor, ex) (0..q_bits - 2).each { |i| arr = nil coff.each { |c| arr = circle_ellipse_intersect(a, b, p0.x, p0.y, len, c) break if arr != nil } return nil, nil if arr == nil p0.x = arr[0] p0.y = arr[1] d = pe.distance(p0) count += 1 break if d < len } return d, count end #given an ellipse and the number of segments (q_bits) covering a quarter of the ellipse, #compute the length of a segment. def self.get_segment_length(major, minor, q_bits, ex) c = circumference(major, minor) #len is guaranteed to be a close over estimation len = (c / 4.0) / q_bits #regress towards the root by adjusting len downwards. Very rapid convergence.. (0..10).each { |i| d, count = test_ellipse(len, q_bits, major, minor, ex) over = (len - d) + (q_bits - 1 - count) * d len -= over / q_bits } return len end def self.get_quarter_ellipse(major, minor, q_bits, len) a = major / 2.0; b = minor / 2.0; d = count = 0 coff = [0.99999999, 0.00000001, 0.5] p0 = Geom;;Point3d.new(a, 0, 0) ps = [p0] pe = Geom;;Point3d.new(0, b, 0) (0..q_bits - 2).each { |i| arr = nil coff.each { |c| arr = circle_ellipse_intersect(a, b, p0.x, p0.y, len, c) break if arr != nil } return nil, nil if arr == nil p1 = Geom;;Point3d.new(arr[0], arr[1], 0) ps << p1 p0 = p1 } ps << pe return ps end def self.get_ellipse(major, minor, q_bits, len) ps = get_quarter_ellipse(major, minor, q_bits, len) ##add the other three quadrants len = ps.length (0..len - 2).each { |i| ps << Geom;;Point3d.new(-ps[len - 2 - i].x, ps[len - 2 - i].y, 0) } len = ps.length (0..len - 2).each { |i| ps << Geom;;Point3d.new(ps[len - 2 - i].x, -ps[len - 2 - i].y, 0) } ps.delete_at(ps.length - 1) return ps end ######################## ######### MAIN ######### ######################## def self.main mod = Sketchup.active_model ent = mod.entities sel = mod.selection ###### USER INTERFACE #### major = 900.mm minor = 400.mm q_bits = 100 #number of segments in a quarter ellipse (-> full ellipse has q_bits * 4 segments) ################# len = get_segment_length(major, minor, q_bits, 0) ps = get_ellipse(major, minor, q_bits, len) ### ADD THE ELLIPSE ## ng = ent.add_group (0..ps.length - 1).each { |i| ng.entities.add_line ps[i], ps[(i+1) % ps.length] } puts 'done' end main end -
A L. Great, that will be very useful in the future. Thanks.
Ps: 2118mm again, How long was my piece of string? -
Use elastic next time Baz then you can get several measurements in one.
-
@box said:
Use elastic next time Baz then you can get several measurements in one.
Which was exactly where I came in...
... everybody chill, it's solved in at least four or five ways, go back to your lives!Thank you all for all your obsessive help.

Baz
PS: It's still a bug.
-
At the maximum display precision of SU with Caul program
2118.238356Nurbs Prog 2118,2799 332 against your theoric 2118.2799 288074484
Sketchup gives 2118,27 6442 with circle 1000 segments!
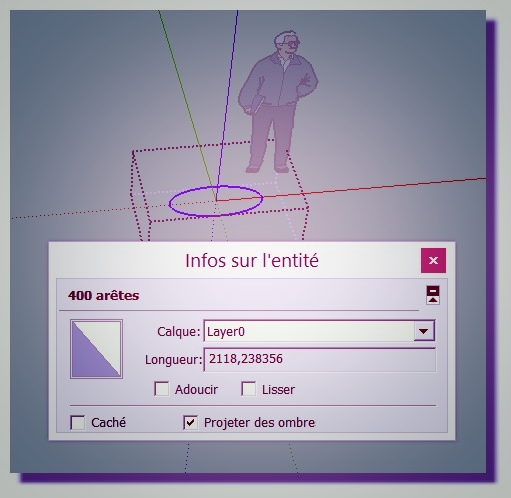
For Baz


-
conjuate ellipse.skpBaz: as noted the model was just proof of concept so not worried about segments yet. the 10X5 (semi) " better model reports 24.227n inches for 1/2 , has only 72 edges and looks very nice.
Some way the number I posted above is not correct so forget about running you calculation. BTW that brings up a question. There are several eliptic intergals and the corresponding polynominal curve fits to those. Do you know which type your equation is for.
Advertisement







