@chippwalters said:
@caul said:
It's actually quite straight forward to construct a "canonical" entasis in Sketchup for any type of column - smooth or fluted. <snip>
I've done two different tutorials on Flowify and even I had a hard time following this, but it is an ingenious use of the tool!
I've added a highly exaggerated example file to show the basic principle.
@pbacot said:
Nice job. Thanks for the line up on plugins! The other day just tried doing a basic tuscsan column (not the first time)and entasis by brute force. I should have used FFD.
It's actually quite straight forward to construct a "canonical" entasis in Sketchup for any type of column - smooth or fluted. Canonical here means the recipe engraved in a wall at the temple of Apollo at Didyma (Turkey) some 2500 years ago. The method below is not exactly as described at the Temple of Apollo, but it's very, very close in practice.
Set out an arc with the Pie tool (as in the first image below). Scale this arc all the way to the top. The resulting elliptical curve is the shape of the entasis. The shaft is usually straight the first third of the height and the entasis is only applied to the top two thirds.
To construct an entasis on a fluted column it's possible to use Flowify twice. From the entasis curve, construct a quaded target surface. Construct a projection surface with the full width of the shaft and every quad with the exact same height as the corresponding quad on the target surface.
Connect and group the surfaces into a Flowify support group. Make a copy of the group and rotate it 90 degrees and place it as in the second image below. Flowify a fluted column through the first support group. Flowify the result through the second support group. The entasis is now applied to both the x and y-dimension. Merge the entasis part into the full column.
@thomthom said:
You need to detect when VfSU loads?[...]
Exactly. When a user loads vfSU dynamically after Sketchup has launched I would like the extension to receive some kind of notification so that the callback can be added. Like an observer listening for an event.
I have an extension that adds a callback to vray. Currently the callback is added in an app observer which fires after all extensions have been loaded. However, if vray is loaded dynamically after Sketchup has started this doesn’t work.
jiminy-billy-bob suggested using a timer which polls vray every N seconds and though this does work there is something not very pretty about it. Ideally I would like to passively listen to vray being enabled and then add the callback. The question is whether there is a way to accomplish this?
If I understand you correctly, this is how I would solve it
The corner "hole" consists of 6 edges (see image). Two edges defines a plane represented by an array of the form [point, normal]. If you have two edges with a common vertex the normal is the cross product of the edges:
normal = e0.line[1].cross(e1.line[1]) plane = [e0.start.position, normal]
Given planes pl0, pl1, pl2 for the edge sets (red, green and blue in the image), you can now calculate the point:
line = Geom::intersect_plane_plane(pl0, pl1) point = Geom::intersect_line_plane(line, pl2)
The point represents the position of your vertex in the corner.
Some final observations and additions.
A skinning method is added to the script so most faces are created automatically. However, since adding geometry with the internal add_face method does not merge stuff properly the resultant group needs to be exploded and regrouped. This will ensure a proper merge. Some holes need to be filled manually. Also, the worm profile must consist of exactly one face for the skinning to work.
When creating a worm the profile will rotate one cog around the main gear center. So, a symmetrical helix requires the profile to be rotated around the main gear center half a cog in the opposite direction. The rotation axis for the worm should be added after this procedure.
This is an intriguing problem. Here's another take.
The first image is a flat setup for flowify and a flowify output which is a gear and a profile for the worm.
The next image shows a setup for a tiny custom script (attached below). The script takes two groups as input:
1) A group with a single edge representing the rotation axis of the
main gear.
2) A group containing the worm profile AND a lonely edge representing the worms rotation axis.
The script itself has two internal parameters at lines 49 and 50. Those are the number of cogs on the main gear and the number of circle segments for the worm.
To run the script, open it in a text editor, set the parameters and save. Then select the two input groups, copy and paste the code into the ruby console and press enter. The result for 48 cogs on the main gear and 192 segments in the worm can be seen in the last image. The output is just profiles that have to be merged manually with Curviloft.
Maybe Flowify can be of help here.
The spiral can be turned into a quad surface with "Extrude Edges by Vector" from TIG's extrusion tools. Just extrude the spiral edges along the blue axis up and down. After that the worm can be mapped onto the quad surface using Flowify.
A problem here is that since the spiral's radius is variable the vertex normals in the quad surface does not extend radially from the spirals center. This means that the distance between two revolutions in the spiral is not retained at the tip. The difference in this case is <1%.
In the upcoming version of Flowify (2.0) it will be possible to explicitly set the normals at each vertex. The image below shows the setup. All normals extend radially from the spirals center and this aligns the geometry at the tip with the geometry at the base between revolutions. The last image shows the difference in a section cut for three consecutive revolutions.
The API documentation recommends 24px for large icons and 16px for small.
On the other hand, in this old thread 32px is mentioned, and there are plugins with 32px icons in their folders. So, what is the correct sizes for icons?
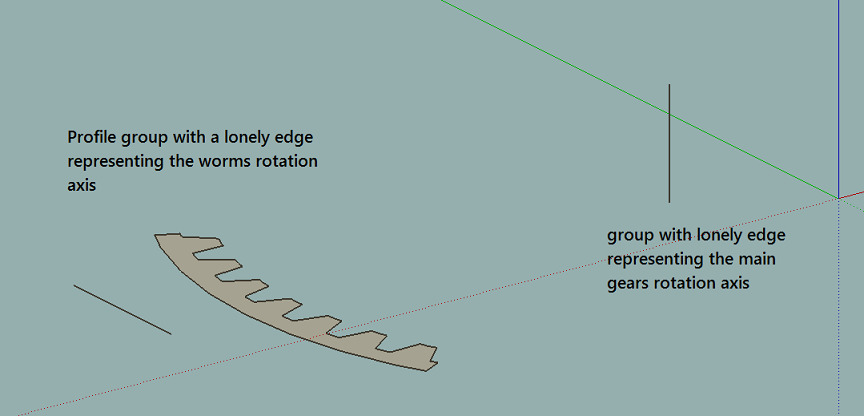
The code below constructs an ellipse in a group centered at origo where all edges have the exact same length. Since the script only computes a quarter ellipse the final full ellipse has an edge count divisible by 4. There's a "user interface" at the end to set major, minor and edge count. The circumference converges to the correct value with increased edgecount.
To run it, just paste the code into the ruby console and press enter.
module CAUL_RegularEllipse
#hack found on the internets. Very accurate...
def self.circumference(major, minor)
a = major / 2.0
b = minor / 2.0
d = b / a
x0 = d**0.5
x1 = d
x2 = d**1.5
x3 = d**2
x4 = d**2.5
s0 = 3929 * x0 + 1639157 * x1 + 19407215 * x2 + 24302653 * x3 + 12892432 * x4
s1 = 86251 + 1924742 * x0 + 6612384 * x1 + 7291509 * x2 + 6436977 * x3 + 3158719 * x4
c = 4 * a + b * (s0 / s1)
return c
end
#find the intersection between a positive half ellipse at (0, 0) and a
#positive half circle at (h, k) with radius r in the first quadrant.
def self.circle_ellipse_intersect(a, b, h, k, r, c)
#start point must be chosen with care so we don't end up outside the domain
x = h - c * r
epsilon = 0.000000000000001
f_e = f_c = 0
(0..15).each { |i|
f_e_sqr = 4 * (a*a * b*b) * (a*a - x*x)
f_c_sqr = 2 * h * x + r*r - x*x - h*h
df_e_sqr = a*a * b*b * (a*a - x*x)
df_c_sqr = r*r + 2 * h * x - x*x - h*h
return nil if f_e_sqr < 0 || f_c_sqr < 0 || df_e_sqr < 0 || df_c_sqr < 0
f_e = Math;;sqrt(f_e_sqr) / (2 * a*a)
f_c = Math;;sqrt(f_c_sqr) + k
df_e = -(b*b * x) / Math;;sqrt(df_e_sqr)
df_c = (h - x) / Math;;sqrt(df_c_sqr)
break if (f_e - f_c).abs <= epsilon
x = x - (f_e - f_c) / (df_e - df_c)
}
return [x, f_e]
end
#given a positive x-value, return the point on the ellipse in the first qudrant
def self.get_ellipse_point(major, minor, x)
a = major / 2.0
b = minor / 2.0
f_e_sqr = 4 * (a*a * b*b) * (a*a - x*x)
f_e = Math;;sqrt(f_e_sqr) / (2 * a*a)
return Geom;;Point3d.new(x, f_e, 0)
end
#return how close the ellipse gets to the endpoint at ex with #bits segments
#of length len.
def self.test_ellipse(len, q_bits, major, minor, ex)
a = major / 2.0;
b = minor / 2.0;
d = count = 0
coff = [0.99999999, 0.00000001, 0.5]
p0 = Geom;;Point3d.new(a, 0, 0)
pe = get_ellipse_point(major, minor, ex)
(0..q_bits - 2).each { |i|
arr = nil
coff.each { |c|
arr = circle_ellipse_intersect(a, b, p0.x, p0.y, len, c)
break if arr != nil
}
return nil, nil if arr == nil
p0.x = arr[0]
p0.y = arr[1]
d = pe.distance(p0)
count += 1
break if d < len
}
return d, count
end
#given an ellipse and the number of segments (q_bits) covering a quarter of the ellipse,
#compute the length of a segment.
def self.get_segment_length(major, minor, q_bits, ex)
c = circumference(major, minor)
#len is guaranteed to be a close over estimation
len = (c / 4.0) / q_bits
#regress towards the root by adjusting len downwards. Very rapid convergence..
(0..10).each { |i|
d, count = test_ellipse(len, q_bits, major, minor, ex)
over = (len - d) + (q_bits - 1 - count) * d
len -= over / q_bits
}
return len
end
def self.get_quarter_ellipse(major, minor, q_bits, len)
a = major / 2.0;
b = minor / 2.0;
d = count = 0
coff = [0.99999999, 0.00000001, 0.5]
p0 = Geom;;Point3d.new(a, 0, 0)
ps = [p0]
pe = Geom;;Point3d.new(0, b, 0)
(0..q_bits - 2).each { |i|
arr = nil
coff.each { |c|
arr = circle_ellipse_intersect(a, b, p0.x, p0.y, len, c)
break if arr != nil
}
return nil, nil if arr == nil
p1 = Geom;;Point3d.new(arr[0], arr[1], 0)
ps << p1
p0 = p1
}
ps << pe
return ps
end
def self.get_ellipse(major, minor, q_bits, len)
ps = get_quarter_ellipse(major, minor, q_bits, len)
##add the other three quadrants
len = ps.length
(0..len - 2).each { |i| ps << Geom;;Point3d.new(-ps[len - 2 - i].x, ps[len - 2 - i].y, 0) }
len = ps.length
(0..len - 2).each { |i| ps << Geom;;Point3d.new(ps[len - 2 - i].x, -ps[len - 2 - i].y, 0) }
ps.delete_at(ps.length - 1)
return ps
end
########################
######### MAIN #########
########################
def self.main
mod = Sketchup.active_model
ent = mod.entities
sel = mod.selection
###### USER INTERFACE ####
major = 900.mm
minor = 400.mm
q_bits = 100 #number of segments in a quarter ellipse (-> full ellipse has q_bits * 4 segments)
#################
len = get_segment_length(major, minor, q_bits, 0)
ps = get_ellipse(major, minor, q_bits, len)
### ADD THE ELLIPSE ##
ng = ent.add_group
(0..ps.length - 1).each { |i| ng.entities.add_line ps[i], ps[(i+1) % ps.length] }
puts 'done'
end
main
end