Scale function
-
Hi all, was just creating a cylinder when the bottom circle stated scaling when I moved my cursor. It did not have a bounding box and scaled proportionately around the central axis. It was possible to make a perfect cone or truncated cone. Could not do it again, can anyone tell me what I did to make it work again? cool tool I never knew SU had

Thanks
-
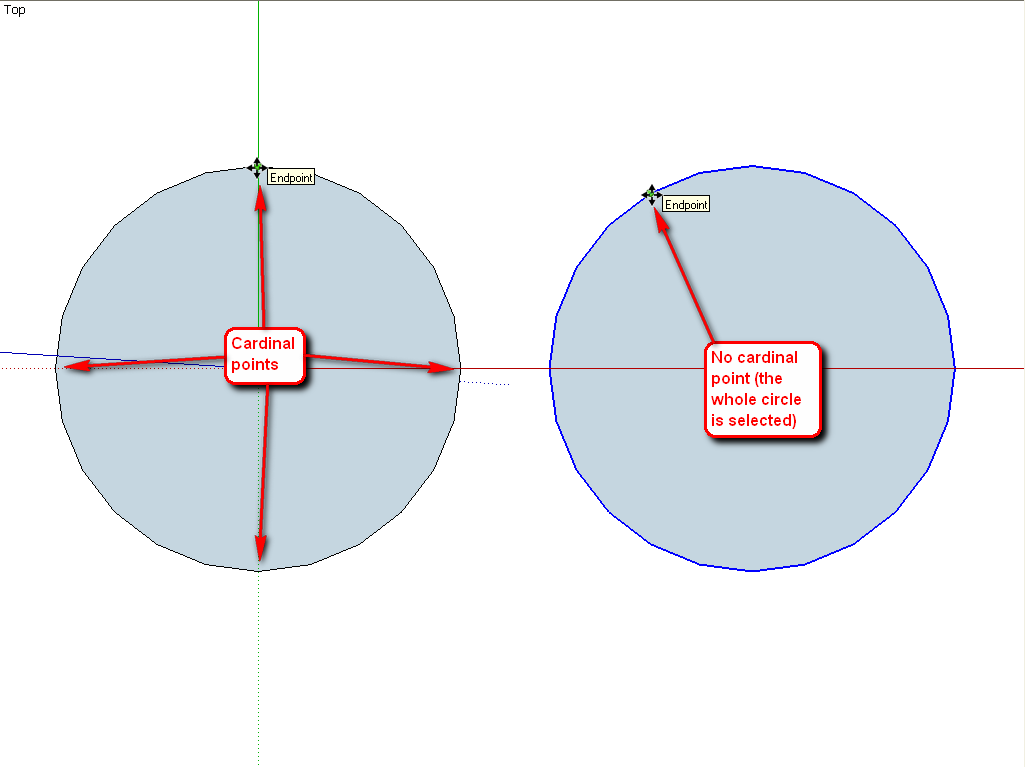
Circles (and polygons and arcs) have "cardinal points". A circle has 4, a hexagon only 2, an octagon 4 again, an arc only has 1 etc.
When you grab a circle (or polygon) at its cardinal point with the move tool, you can scale it (around its center) and can modify the bulge of an arc this way.
One cardinal point is always "placed" at the point where you drag out the circle/polygon/arc. The others are distributed evenly (a default circle has 240 segments so the are distributed at 90 degrees to each other).
When you try to grab another end point on a circle, the whole circle is selected and you will move it rather than scaling.
-
-
And with plugins what, dear Pilou? Steve did something in SU he did not understand. You cannot suggest a plugin instead of telling him what he did!

-
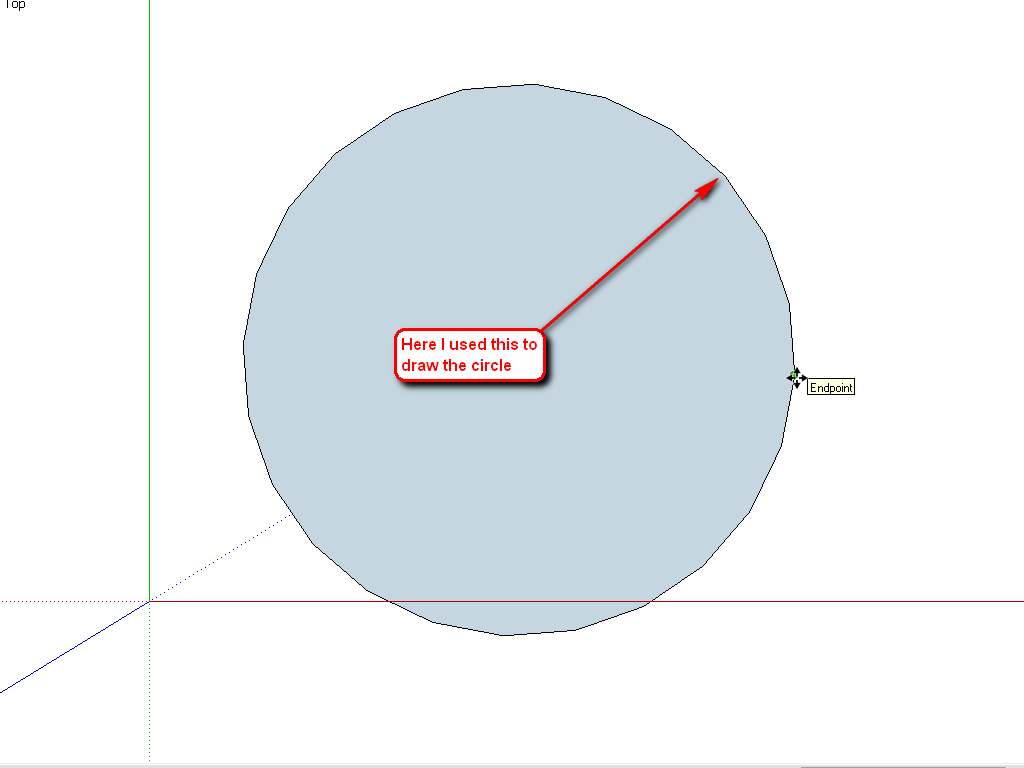
Thanks Gaieus, I could only find the points on a circle when I create the circle with a start point on the axis intersection point. When I create one away from that point I am unable to identify any of those points is there any other way to identify them?
-
Hm. I seem to have been wrong where those points are (when saying that one is what you use to draw the circle with). It seems that the one that is on (or nearest to) the axes.
-
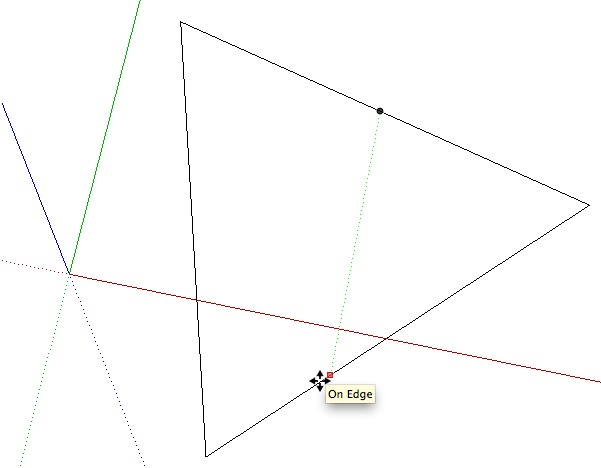
The cardinal points are always located at the points where lines parallel to the axes would cross the edge. Note that it may not be on a vertex or the midpoint of an edge.
-
Thanks but have discovered the answer: if you move the cursor around the circumference it highlights the circle in blue however when the curse is moved over a point at which you can scale this way the highlight will momentarily disappear, foolproof and cool but I can only find 2 such points on any cir
 cle
cle -
There are four cardinal points. Draw a circle dragging the radius so it is parallel to an axis. This will make finding the cardinal points easier. Then hover the Move tool over the vertices at the 12, 3, 6 and 9 positions. Or better, N, E, S and W, since they are called "Cardinal Points".
-
Hi Gaieus, hi folks.
@gaieus said:
One cardinal point is always "placed" at the point where you drag out the circle/polygon/arc. The others are distributed evenly (a default circle has 240 segments so the are distributed at 90 degrees to each other).
I though that default segmentation was 24 for circles

Just ideas.
-
Thanks all, good stuff.
-
@unknownuser said:
And with plugins what, dear Pilou? Steve did something in SU he did not understand. You cannot suggest a plugin instead of telling him what he did!
@unknownuser said:
It was possible to make a perfect cone or truncated cone. Could not do it again
Seems he was in pain so seems to me that was the more speedy as emergency!

-
@jean lemire said:
Hi Gaieus, hi folks.
@gaieus said:
One cardinal point is always "placed" at the point where you drag out the circle/polygon/arc. The others are distributed evenly (a default circle has 240 segments so the are distributed at 90 degrees to each other).
I though that default segmentation was 24 for circles

Just ideas.
ah, come on, Jean. that's obviously a typo.

-
[off:2b45bxhe]Yeah. It's just a typo. The 4 and 0 are really close together on the keyboard.
 [/off:2b45bxhe]
[/off:2b45bxhe] -

-
[off:3hgvniwx]

[/off:3hgvniwx] -
@dave r said:
The cardinal points are always located at the points where lines parallel to the axes would cross the edge. Note that it may not be on a vertex or the midpoint of an edge....

Depending on the number of segments in a circle, there are two or four cardinal points.
a) if the number of segments is uneven then there are only two cardinal points: one is a vertex, the other is the midpoint on the edge opposite to that vertex.
b) if the number of segments is even, then there are four cardinal points. If the number of segments is divisible by four, then all four cardinal points are vertices, equally spread around the circumference.
Otherwise, (even but not divisible by four) there are two cardinal vertices 180 degrees apart and two cardinal midpoints "on edges in between"
This is about the number and how they are spread over vertices and midpoints.
To find the first cardinal vertex (there is always at least one!) on an ungrouped circle in the R/G plane, it is located at the eastmost position on the circumference of the circle, concidering unchanged axes. So the systems axes are important. Not the changed axes.
On circles in other planes and/or in grouped context, just try to find out, I haven't (yet!?). -
Hi all, just in case the point was lost, the easiest way to locate a point at which to scale the circle is: hover the cursor over and around the circumference of the circle, (with the move function engaged) the points at which the blue circle "clicks off" (turns black) is one of the points at which you can scale the circle.
Advertisement







