Mini-challenge
-
@pbacot said:
Well if you had a true arc or circle you could find your exact intersection points. But there are no true circles in SU.
right, that's the brute force method i mentioned above.. make a little arc with a thousand segments and it will work..
-
@unknownuser said:
@pbacot said:
Well if you had a true arc or circle you could find your exact intersection points. But there are no true circles in SU.
right, that's the brute force method i mentioned above.. make a little arc with a thousand segments and it will work..
That sounds dangerous - most likely you'll get some minor accuracy issue somewhere ~0.00001 of whatever - something that eventually cascades into a nightmare! (thinking of all them imported AutoCAD plans I've had... x_X )
-
@thomthom said:
@unknownuser said:
@pbacot said:
Well if you had a true arc or circle you could find your exact intersection points. But there are no true circles in SU.
right, that's the brute force method i mentioned above.. make a little arc with a thousand segments and it will work..
That sounds dangerous - most likely you'll get some minor accuracy issue somewhere ~0.00001 of whatever - something that eventually cascades into a nightmare! (thinking of all them imported AutoCAD plans I've had... x_X )
yes.. that can happen and why i eventually went with a dynamic component instead (maths)
for getting an accurate enough dimension for a framer to cut.. it's ok.. but to have something like that in a drawing where you may be inferencing etc for future parts of the drawing.. i agree, it's a no-no.. you can throw off everything else down the line..
-
From tip to tip you have length A-C the hypotenuse on the board. You know the width of the board B-C so you can find A-B. So when you have a board A-B long exactly you can rotate it with snaps then trim it, but is the rotate operation inaccurate?
-
@pbacot said:
From tip to tip you have length A-C the hypotenuse on the board. You know the width of the board B-C so you can find A-B. So when you have a board A-B long exactly you can rotate it with snaps then trim it, but is the rotate operation inaccurate?
rotate is accurate.. you just need something to snap to which is hard to get in this case..
but what you're saying.. can you do that geometrically (as in, can you do it using only sketchup tools) or would you need a calculator?
(currently, the only way i've been able to do it is with a calculator (well, i use the DC dialog for the calculator that can then adjust the position of lines)) -
Cursed this challenge! Now it really bothers me that I cannot find an easy way for this in SU.
I'm not even quite sure how to calculate the angel... ? -
Yes, it's a pity that true geometry is impossible in SU and one always needs to rely on workarounds. In this "rotation" workaround you still get a 0.01 cm (0.1 mm) inaccuracy which is obviously okay for constructing but annoying to know there is in your model since you never know when exactly you'd need that accuracy for inferencing.
I have drawn two guides at 5 (well I used cms but who cares) apart and then tried to rotate them but as you can see, although I do get the endpoint inferencing, SU actually does not know what it is inferring there along the guide.
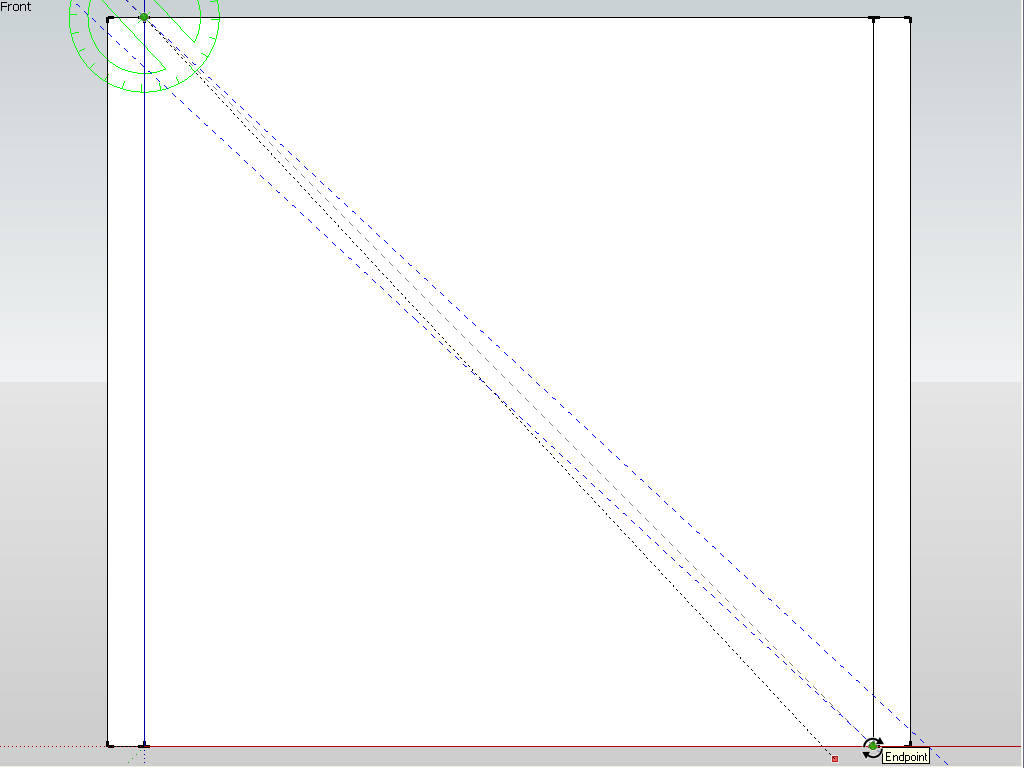
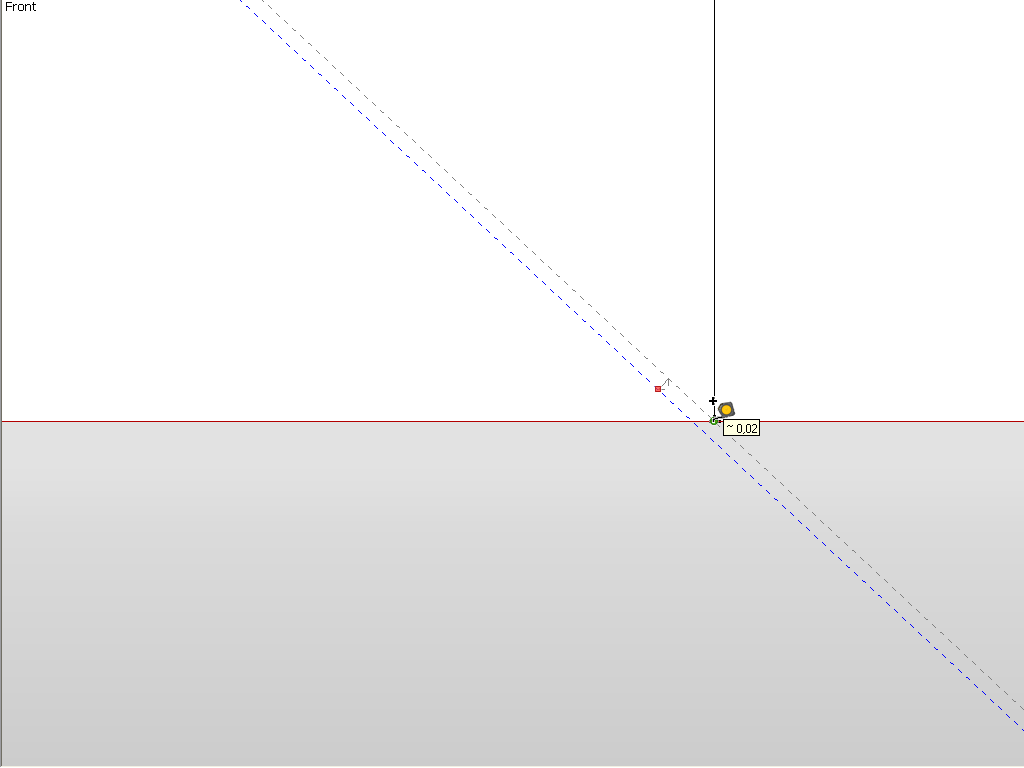
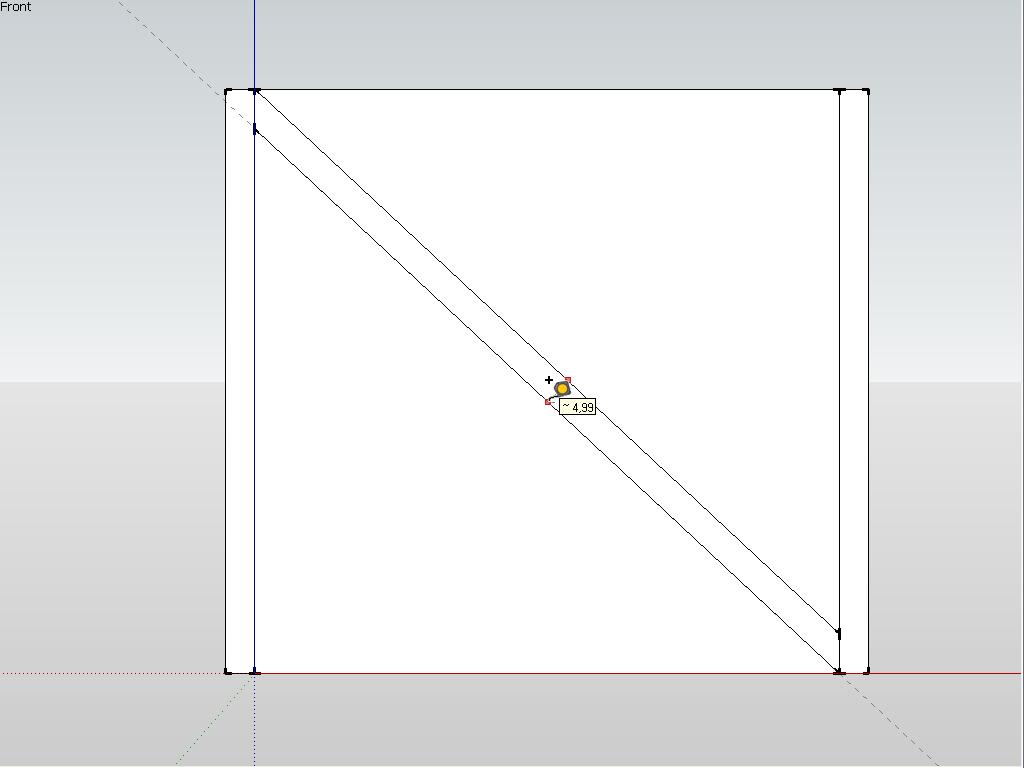
-
-
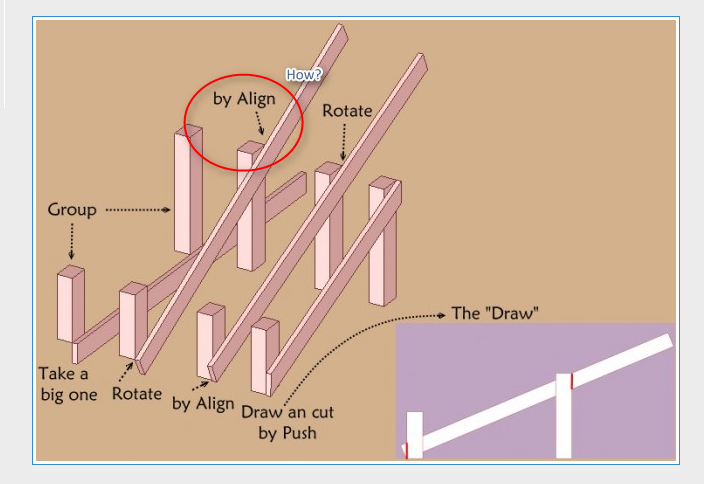
Like in reality what more simple without any Plugin ?

The big one is of course any what you want!
Groups are any size!
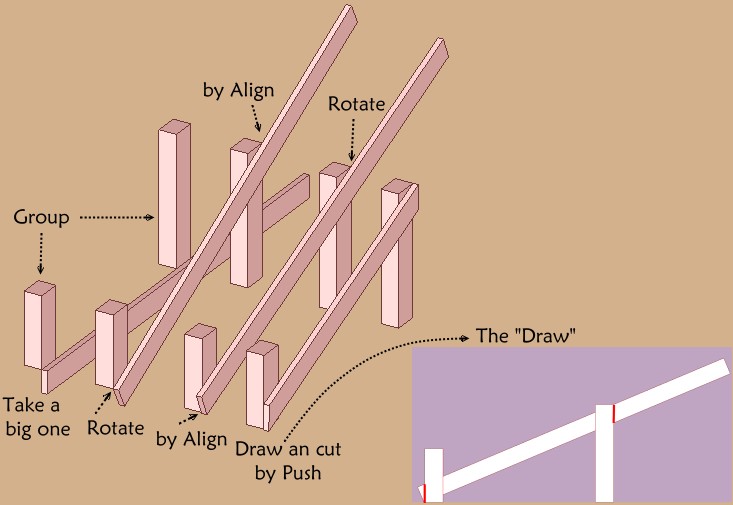
-
@gaieus said:
I have drawn two guides at 5 (well I used cms but who cares) apart and then tried to rotate them
What where you snapping to/with?
-
It's in the screenshot. But note that no matter how "close" you seem to snap along a guide (or any edge), it will never be accurate (second screen shot). The cursor is "sliding along" the guide and does no give an accurate inference.
-
@unknownuser said:
Like in reality what more simple without any Plugin ?

The big one is of course any what you want!
Groups are any size!
[attachment=0:1cpfqa3m]<!-- ia0 -->general.jpg<!-- ia0 -->[/attachment:1cpfqa3m]Wooh! Now I understand. I just didn't notice how you originally aligned the board.
-
@unknownuser said:
How ?
By the simple use of the Rotate tool !!!

And that will be the same for the second rotation
Just put the Rotation tool on the other group's axe and rotate the view for snap on the good point!
So you can now draw the 2 little segments for the Push cut!
Any calculate was tourmented during the movie!

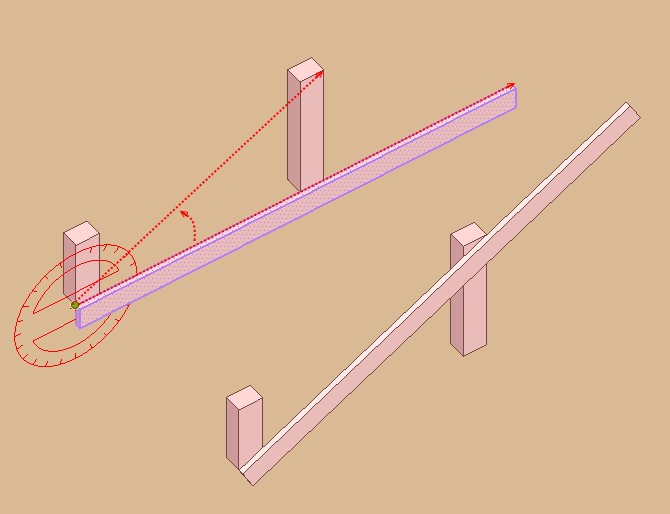
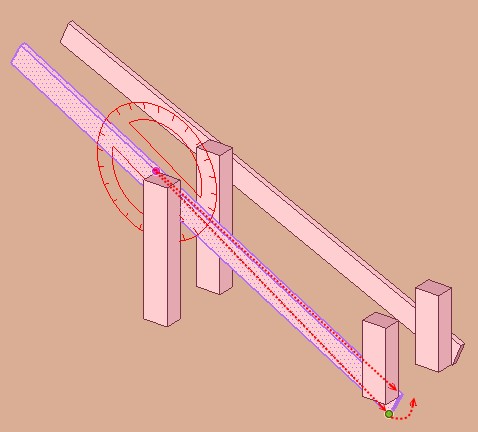
-
@pbacot said:
Well if you had a true arc or circle you could find your exact intersection points. But there are no true circles in SU.
My 'TrueTangent' tools have various options, in this case you could place a cpoint exactly at the 'true-intersection' of two SUpArcs...
-
@unknownuser said:
it will never be accurate (second screen shot). The cursor is "sliding along" the guide and does no give an accurate inference.



That will say that any rotation can be made precisely?


You can make zoom during the process!
And re look my last image, there is green point that indicate that the snap is done!
And a red one will be drawn at the end of the last snaping on the group!What do you want more accurate ?

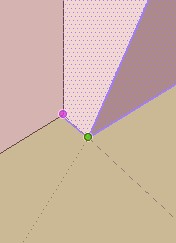
I have verified! Seems you right!
That is very ennoyous and want to say that any constructions made with align / Roation are false!
Another headache to resolve!

-
Jeff, I've had to draw diagonals like this a number of times and not found an elegant solution. It's always been via brute force. I forgot about TIG's True Tangents.
-
@dave r said:
Jeff, I've had to draw diagonals like this a number of times and not found an elegant solution. It's always been via brute force. I forgot about TIG's True Tangents.
Pilou's method was quite easy and simple. And also accurate!
-
@thomthom said:
@dave r said:
Jeff, I've had to draw diagonals like this a number of times and not found an elegant solution. It's always been via brute force. I forgot about TIG's True Tangents.
Pilou's method was quite easy and simple. And also accurate!
Yes, his way works, sort of. The second rotation is not perfectly accurate, though. I meant to simply draw it in place.
-
-
Nice challenge by the way, at first I thought this should be easy but then...
You can also perform the rotation as a tangent to the drawn arc, (referencing the vertices on the arc). Of course it is not exact but the angular error is vanishingly small (approximately a^2*t/l ; t,l thickness and length of the rail, a is angular resolution on the arc (total angle/number of segments) in radians)). The final rotation accuracy increases with the square of the number of segments on the arc. After a few hundred segments SU makes the structure ideal at explode.
Ogan
Advertisement







