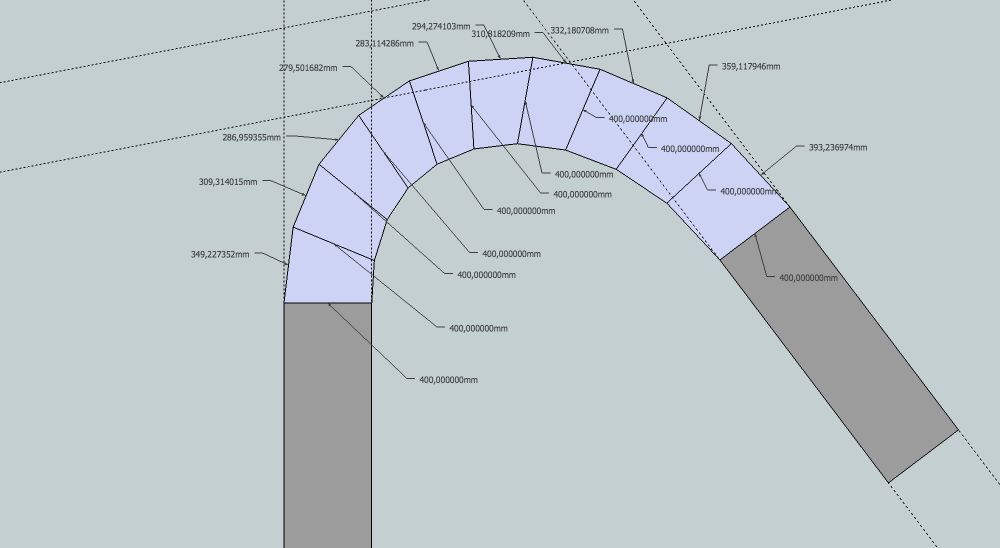
Sketchup is Inacurrate???

mitcorb

I have been following this thread. And I care, if it is do-able.

pilou

You then need to shorten the road on the left AND increase the radius !

Robust again

So if for any reason I don't want elongate or shorter in straight line pieces of road on the left and the right connection with tangency is impossible ?

Said a "plumber" who has not straight tubes but any curvated one

jgb

@unknownuser said:

Despite of all that, what is the best connection between 2 parts of any inclined roads on a flat terrain?

This is a standard "OGEE" Curve problem of joining 2 non parallel roads.

Did it in High School (that's 53 years ago ) with pencil, compass, slide rule, protractor and ruler. No such thing as a pocket calculator then, let alone Sketchup.

But damned if I could remember how I did it!!!

Played in SU for 29 min and got nowhere.

So the attached drawing is a "Sketch" of what the solution would be.
Not calculated, just by eye.
The "road" rectangles are drawn overlaid on Pilou's ROAD.JPG.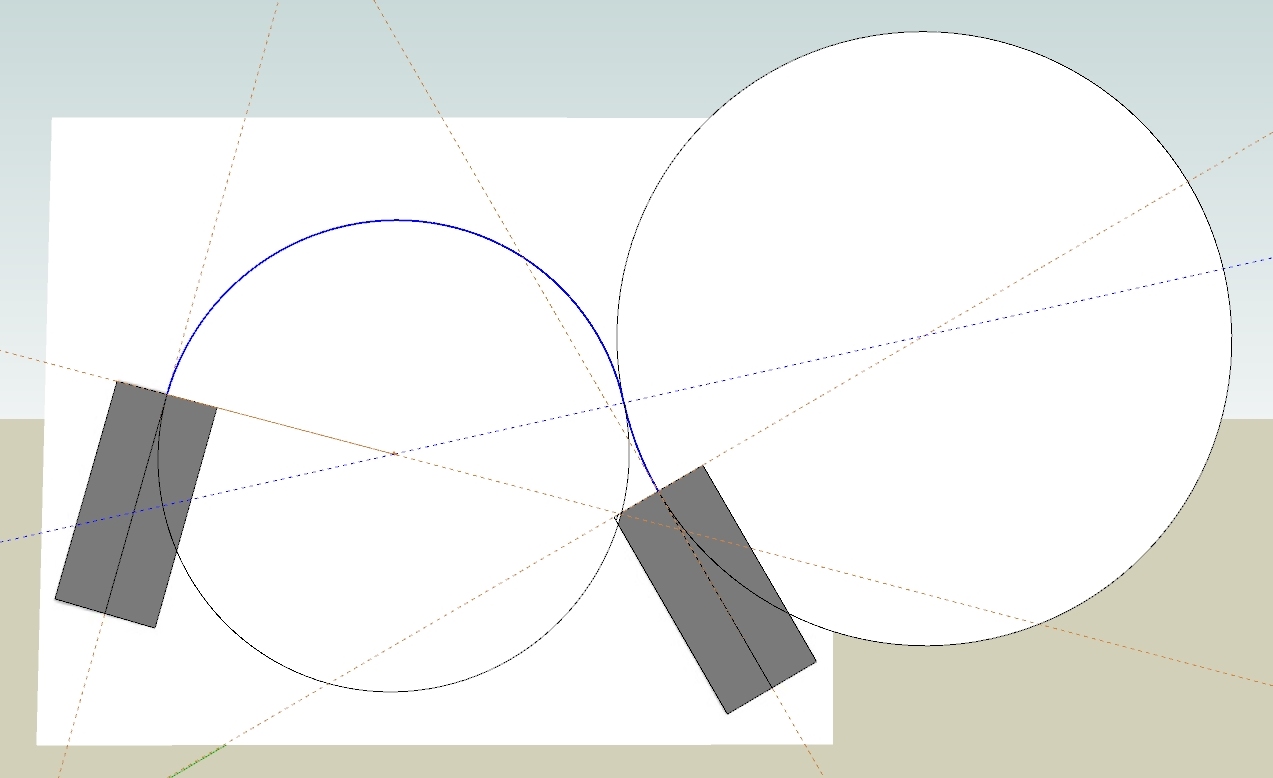

This is a sketch of a solution, not an accurate drawing.

jeff hammond

@unknownuser said:

Despite of all that, what is the best connection between 2 parts of any inclined roads on a flat terrain?
(in any progs of course just in theory with same width on the path)

Compass+ Protractor + Set Square + Ruler
Arc circle + tangency
Blend + tangency G1, g2, g3...+ Bulge
Fillet G1, g2, g3...+ Bulge
Sweep variation
Conics
Offset of one jointure
From a joined yellow line then propagate a perpendicular width segment
...
(here connection wanted on the top)

in sketchup, you can use bezierSpline to get a tangent b-spline for one connection.. as far as accurately offsetting that curve, i don't know how to.. the maths go beyond my knowledge at that point and i'd rather just have software do the proper calculations for me
(and actually, i don't know the maths to even see if the sketchup drawn b-spline is in fact correct.. and this is an instance where, to me, it's required that i'm using an app that i can fully trust to give the right solutions.. goes back to what i was saying about knowing the numbers.. i don't know the numbers here and neither does the app so i'm screwed..)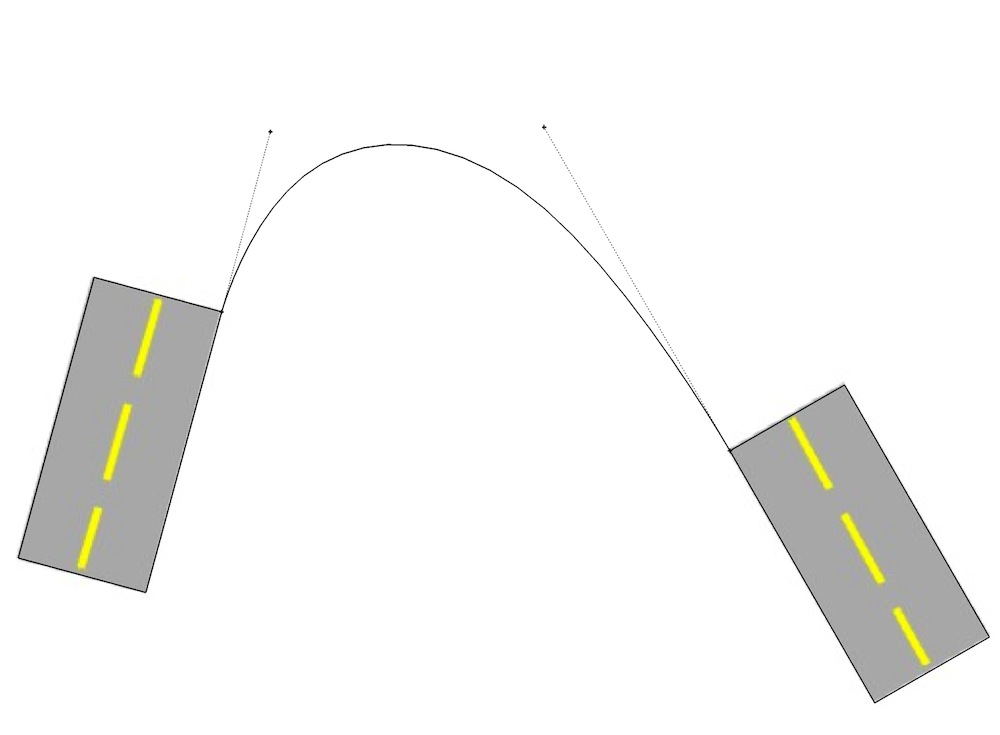

• draw an extended line to the one you would like to connect tangentially to..
• using uniform B-spline set to an order of 4 at least, make 4 clicks, (first tangent point, end of it's extended line, end of the other side's extended line, second tangent point)

but assuming that curve is in fact correct, i have no idea how to proceed with offsetting properly (as in, arcs are easy to understand.. these types of curves?.. well, let's just say i was never taught about them in school..

but hey, in sketchup, i could definitely come up with something that looks ok..

pilou

Seems very cool too!

jeff hammond

@jgb said:

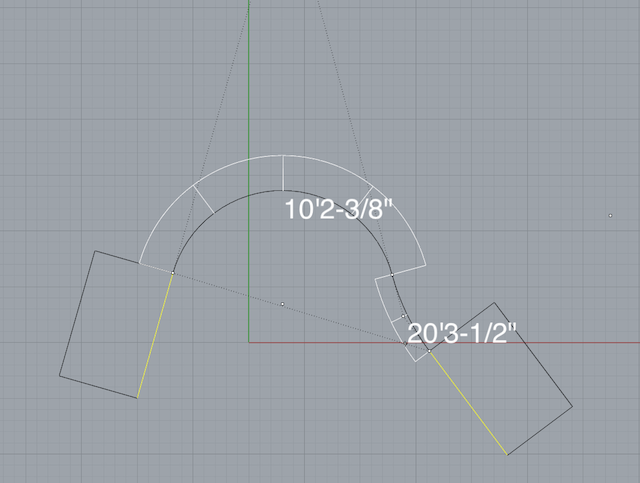
Played in SU for 29 min and got nowhere.

or, using the ArcBlend command, you'd play with it for 29 seconds and see all possible solutions..

Screen Shot 2013-01-29 at 1.10.16 PM.png

jeff hammond

@unknownuser said:

Seems very cool too!

oh. i thought that was a standard approach in france.. don't all the roads look like this over there?

gilles

Sorry Driven but already done
http://sketchucation.com/forums/viewtopic.php?f=15&t=44142&start=480#p453462

But
@unknownuser said:

pilou wrote:
And if for any reason I don't want elongate in straight line the piece of road on the right ?

pilou

Damned: Imperial measures can be readable as hours minutes second!
(maybe it is ? )

The funny thing is that tool who is named in Fance "pistolet" (pistol, gun)

is named on the new world a "French Curve" I don't know why! ?

driven

@gilles said:

Sorry Driven but already done :mrgreen:

back to the round about then... cheers

gilles

With bezeir classic + component stringer + polyline= tedious.

bezier-road_V6.skp

driven

a more serious reply... for an even curve from both directions. I did trim the fussy edges...
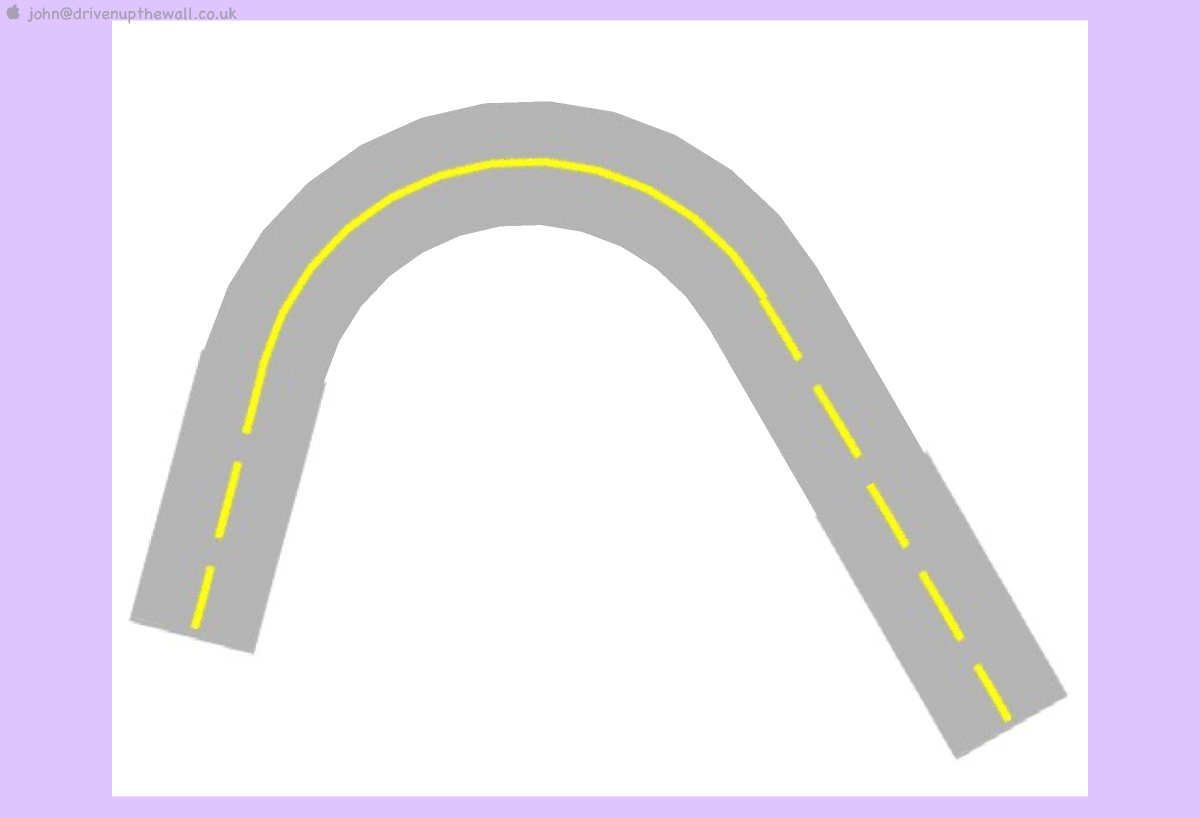
john

edit.. took the skp off as it's a repeat of earlier offer.

jeff hammond

@gilles said:

With bezeir classic + component stringer + polyline= tedious.

here's one done in rhino then brought into sketchup and segmented.. it looks as if this version has the 5m crosslines perpendicular to the curves whereas yours look to be leaning..

thing is, i can't figure out how someone could calculate where exactly perpendicular to a curve like this is in a polygon app.. have a look at this .skp and see if you can find any sort of method/reasoning to achieve it manually..

bez0ffset.skp

as far as i can gather at this point, the best we could hope for in sketchup along these lines would be some sort of educated guess ?? (actually, i bet it's possible to do it accurately with a segmented modeler but at that point, the app would have enough info to display the true line so why bother segmenting it)

jeff hammond

.

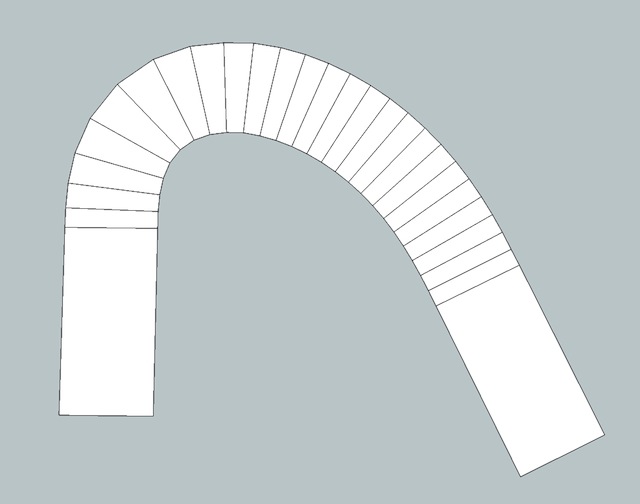
here's another example of sketchup acting in an intelligent manner with regards to its arcs..

if you use the arc tangent snap on another arc, it acts appropriately and accurately..
then explode the other arc and you'll see it gives a different result (the correct result for that situation)..

i was a bit surprised to see sketchup handle this properly (it's different than other 'smart' examples i've given because in this case, sketchup is correctly identifying whether pre-existing geometry is an arc or a series of edges (even though the look identical) then reacting accordingly

but it's a good example of how sketchup could also be identifying whether the user has an arc or edges drawn prior to offsetting/followme_ing and reacting correctly..

jeff hammond

.

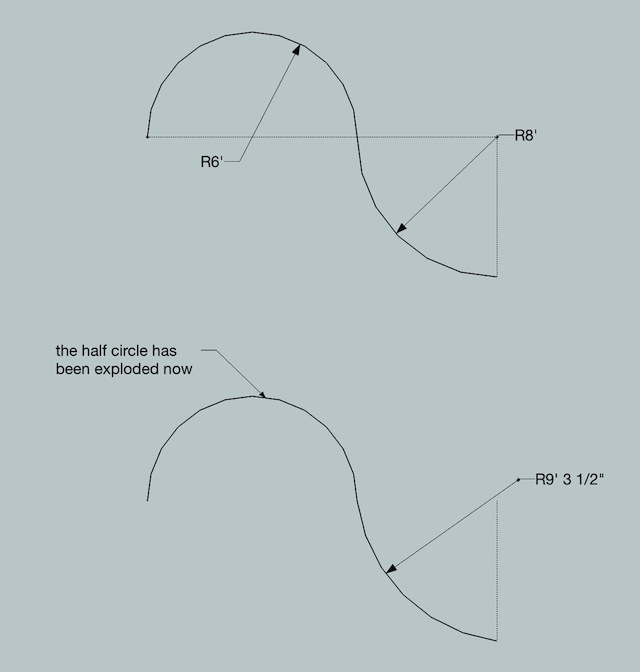
or maybe showing it this way makes it more clear..

the top row consists of the same radius half-circle with the only difference between the three being the number of segments in the arc (2, 6, & 12 segments)

i then drew tangent arcs using the arc tool's tangent snap.. notice all three radii are the same.. (it wasn't paying attention to the half-circle's segments.. only the fact that it was an arc entity that it was connecting to)

the bottom row is a copy of the top row except the half-circle have been exploded into individual segments..

trying the same thing with the tangent snap now considers only the last segment and goes tangent off it..

jgb

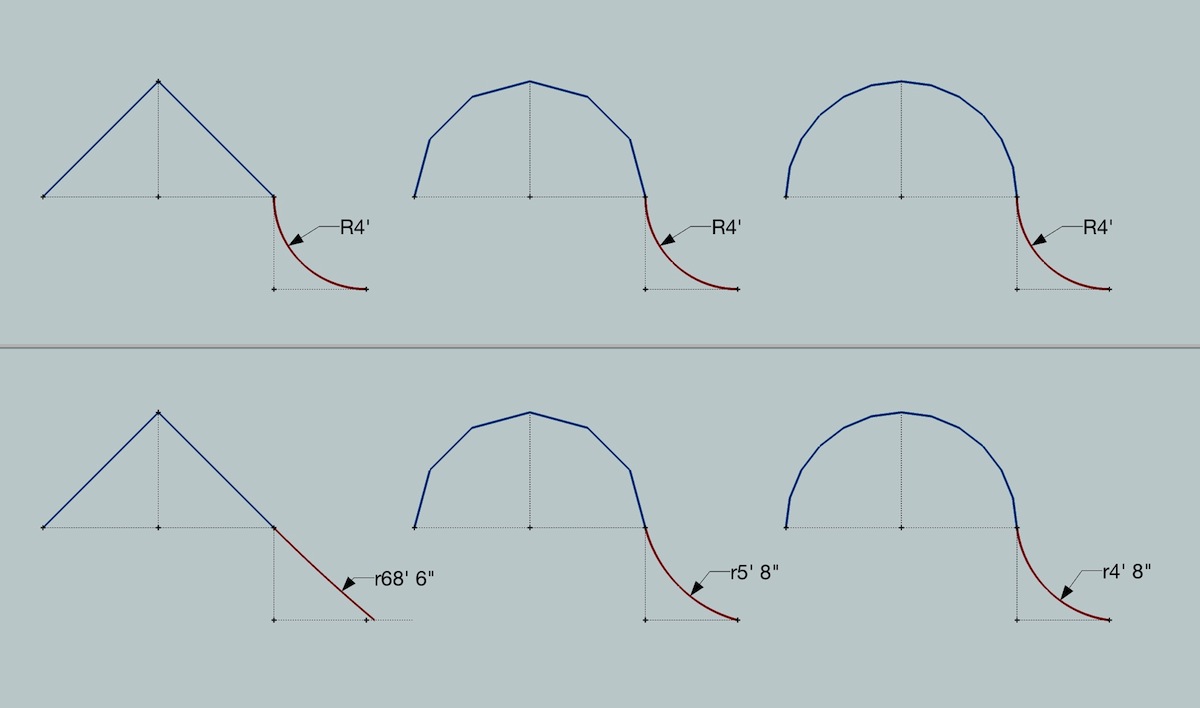
Using Bezier curves does create an elegant solution, BUT, NOT for real road design. You do not want a changing curve for a real road, as most drivers would not be able to accurately (and safely) negotiate the curve. That is the reason why road curves are mainly true circular arcs; they are a constant turn angle for the driver. Aside from that, road construction is easier and cheaper.

Take a look again at Pilou's picture of the winding mountain road. All the curves are circular arcs. Using Bezier curves would have made a nicer looking road, but far more difficult to drive on (as if THAT road were easy ).

pilou

Judicious remark !