[Plugin] TrueTangents v3.0
-
This Ruby Script now provides 5 new functions - 'truetangents', 'commontangents', 'trueintersections', 'tangentialarcs' and 'filletarc' - it has plugin sub-menu item 'Tangent-Tools...' or you can type the names to run it from the Ruby Console. It's written to work on a selection BUT could be reconstructed as a cline/arc method if thought useful...
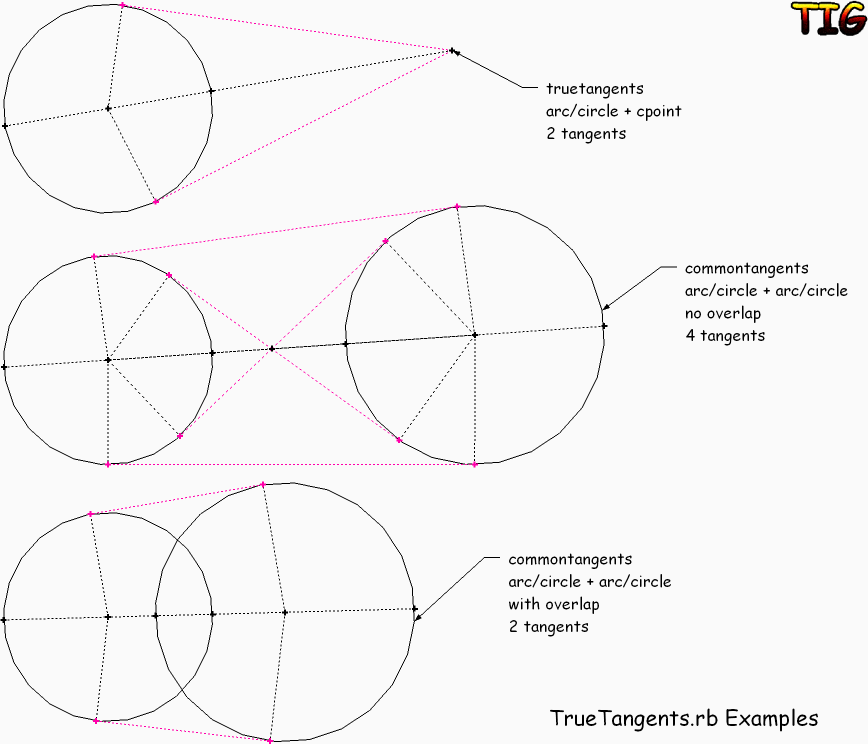
True Tangents = truetangents
Select an arc/circle and a cpoint (aka guide-point)
Run truetangents
On errors - e.g. no arc selected or the cpoint is inside the circumference - there is a console message.
It then draws cpoints at the arc-centre, circumference and the 2 tps, and clines on the two radii and tangents - it draws to the true tps - these might not be on the arc itself if it's lightly segmented - now you can rotate, entity-info increase segments or reconstruct the arc as desired so it passes through a tp...
Common Tangents = commontangents
Select an arc/circle
Select a second arc/circle
Run commontangents
On errors - e.g. 2 arcs not selected or a circle within another circle can have no common tangents - there is a console message.
It then draws cpoints at the arc-centres, circumferences and tps, and clines on the four radii and two/four tangents - it draws to the true tps - these might not be on the arc itself if it's lightly segmented - now you can rotate, entity-info increase segments or reconstruct the arc as desired so it passes through a tp... Different forms of common tangent are produced if the arcs are separated by clear space or intersect (4 or 2 nr)...
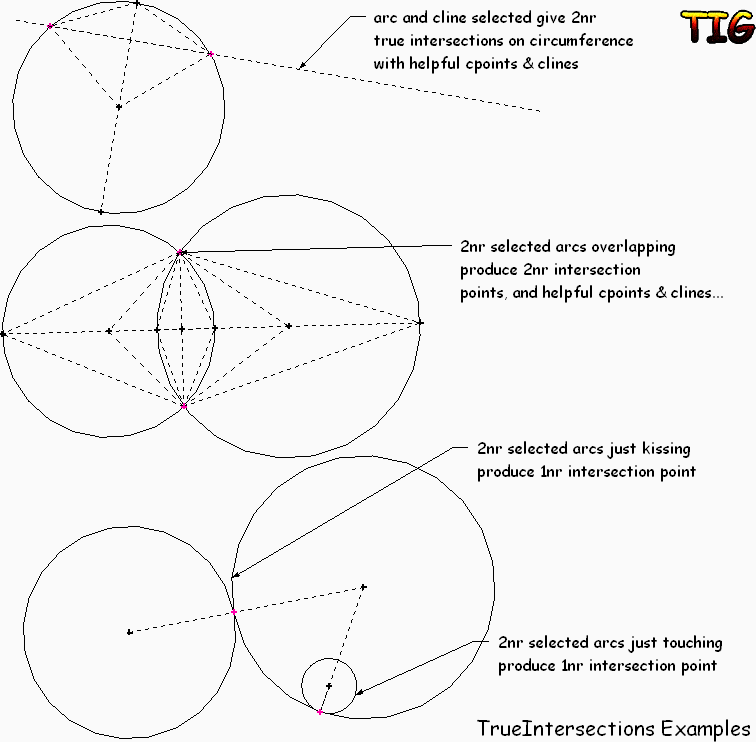
True Intersections = trueintersections
Select an arc/circle
Select a cline OR a second arc/circle
Run trueintersections
On errors - e.g. non-intersecting arcs/clines - there is a console message.
It then draws 2 cpoints at the true intersections of the arc and the cline [OR the 2 arcs]; it also adds further centre-points, clines etc and additional true mid-points on the circumference to aid with later arc recreation if desired: special cases produce other drawn results - e.g. cline is a diameter, arcs just kiss or touch at one point...
Tangential Arcs = tangentialarcs
Select a Line and an Arc or Circle
Run tangentialarcs
On errors - e.g. non-intersecting arcs/clines - there is a console message.
It then draws cpoints at the centers of the two tangential-arcs [or one tangential-arc and another looped tangential-arc] and at their tangent-points etc, [messages in console], it also adds clines on the radii to the tangent points-etc. If the line is tangential to the arc or if the tangential arc's radius would be > the arc_radiusx100 or smaller than 1/100th then no cpoint is drawn at the center because it might be many miles away and effect the model's extents - instead a cline is drawn between the line end and tangent-point and a console message suggests you might like to draw a straight line instead... The tangential arc cpoints etc are added at the end of the line nearest to the arc, unless that end is on the circumference, then the other end is used. Internal lines also have tangential-arcs and are created similarly at the end nearest the circumference unless it's touching it...
Fillet Arc = filletarc
Select an arc/circle and a cline/line (aka guide-line)
Run filletarc
On errors - e.g. no arc selected - there is a console message.
Enter the required fillet radius in the dialog that appears. If the line doesn't intersect the arc and the fillet radius won't work then you are told and the dialog reopens giving the minimum radius that will work... Assuming the radius is valid then it draws cpoints at the arc-centre, the new fillet arcs' centers and all of the the true tps, with clines on the each of the two radii and the chord linking the pairs of tps - note how these might not be on the arc itself if it's lightly segmented - there are 4 or 8 possible fillet arcs depending on whether or not the line intersects the selected arc, draw over the one(s) you want using the 2D Arc / Circle Tool etc...
EDITS:
v1.1 now adds all 4 common-tangents for non-overlapping circles
v1.2 glitch on some external common-tangents permutations fixed
v1.3 additional cpoints added at circumference intersections to aid arc redraw though 3 points if needed
v1.4 extra cpoints/clines added to opposite circumference intersections to aid arc redraw in other direction
v1.5 true intersections added for arc+cline OR arc+arc
v1.6 tangential arcs added for line+arc
v1.7 fillet arc added for arc/circle + line/cline, dialog to enter fillet radius
v1.8 missing 5th menu item fixed
v1.9 sub-menu 'Tangent-Tools...' added
v2.0 tolerance added on the coplanar check for arcs
v3.0 Float 'n1=~n2' replaced with 'eq(n1,n2)' avoiding potential clashes.


More info here http://sketchucation.com/plugin/771-truetangents
Please get the latest version from the PluginStore...
http://sketchucation.com/pluginstore?pln=TrueTangents -
TIG, Thank you so much. Look forward to giving it a try. I appreciate your generosity in sharing this.
-
TIG,
True tangents worked fine, couldn't get common tangents to execute.
-
@ben ritter said:
TIG,
True tangents worked fine, couldn't get common tangents to execute.
Same here
Bep
-
commontangents - are you selecting two arcs / circles that are as the image ?
The images were made from SUp 7 using the tools... Arcs/circle must be coplanar - what's the Ruby Console error message ? -
TIG, thanks - both methods worked fine for me.
-
It now worked after closing and re-opening SU.
-
Is there any way to get the outside tangents, as in your overlapping example, without overlapping circles?
-
I've added the 2 'external' common-tangents to the non-overlapping version... Thanks for the feedback.
Find v1.1 here: http://www.sketchucation.com/forums/scf/viewtopic.php?p=160780#p160780
-
I've just found an error in certain combinations of arc radius and rotation in 3D. Sometimes the common-tangents weren't drawn right... Found a fix... here's update v1.2
http://www.sketchucation.com/forums/scf/viewtopic.php?p=160780#p160780 -
Thank you, Tig!
I was waiting for longtime for tools like this one, helping the 2d drafting directly in SU.
I also claimed for years for better native SU 2d drafting tools, but it seems that AutoCAD still has some magic attraction, although buying it only to use its 2d capabilities seems to me a waste of money
The bad news, though, is that TrueTangents makes my SU 7 to end with bugsplat on initializing
 It surely is a ruby conflict, because deleting it solves the issue - actually I have no more than 10 or 12 ruby installed).
It surely is a ruby conflict, because deleting it solves the issue - actually I have no more than 10 or 12 ruby installed).
I'll try to find out where the problem is. -
Thank you very much for this TIG. This will come in very handy.
-
Thanks a bunch TIG, now a simple thing is truely simple.
I confirmed it works on Macs.
-
Thank you, TIG!
I missed this tool a lot of times in the past.
And a special thank you for making it work in SU5 and on the mac!
Jörg -
Nice one TIG, thanks a lot!
-
GREAT PLUGUN!, thanks a lot!
-
very usefull !!
Thanks TIG
erikB -
Here's v1.3... http://forums.sketchucation.com/viewtopic.php?p=160780#p160780
I've added some more cpoints - at the intersections of the circumference(s) and the line from cpoint-to-centre or centre-to-centre - these can be useful if you want to redraw an arc through three points from tp to tp quickly with the same radius... -
Here's v1.4 http://forums.sketchucation.com/viewtopic.php?p=160780#p160780
It's updated to have extra cpoints/clines on the opposite sides of the arcs' circumferences - now to aid in possible redraw in both directions of arc's curve... -
TIG,I wanted a celebration, this plug-in.
The traditional skills are essential to kikujutu Japan.
Advertisement







