Is There Any Way to Make This?
-
First of all, I would use a circle with a segment count that is divisible by ten (around the cinquefoils, there are those ten pikes or what that should conveniently adjust to the segment count of the surrounding circle). Then of course you still need some bulging - say at least 3 segments between each - that would be 30 segments for a circle. Or 40 maybe but considering the overall complexity of the whole shape, I would not go over that.
-
@gaieus said:
First of all, I would use a circle with a segment count that is divisible by ten (around the cinquefoils, there are those ten pikes or what that should conveniently adjust to the segment count of the surrounding circle). Then of course you still need some bulging - say at least 3 segments between each - that would be 30 segments for a circle. Or 40 maybe but considering the overall complexity of the whole shape, I would not go over that.
Thanks for the suggestion on the segment number; by default, I use powers of 2, but I'll go with 30. Still not sure how I would go about making the circle, though, which was my original question (sorry if it was unclear). I can't figure out how to find the center point nor the length of the radius (although I could make it if I had either). In case you're curious, I'm assuming the diameter of the main circle is 16 units.
-
Just to clarify; we are talking about the four, smaller things in the corners now, right? (Otherwise quite strange shape; the main, big circle has 16 "petals" and it would be extremely hard to combine it with a number of 30).
I also like the way SU currently has the segment count as it is conveniently divisible with many things (but 5)
So you ean you cannot find the centerpoint of the circle? Or cannot define a radius or it?
-
So the circle needs to be tangent to the 3 points of contact...maybe this will help?
Tig's True Tangent http://forums.sketchucation.com/viewtopic.php?p=160780#p160780
-
maybe these will help?
-
I wouldn't know how to calculate the radius or diameter to fit into the specific area, but I fooled with the geometry until I found a working method. I figured medieval architects were fond of arcs and circles to create things, so it should be possible to decipher it with the same tools. It calculates to 0.574468085106383 of the distance which is a bit useless of a number, but to make it fit perfectly I just used lines and circles. Basically 3 circles to midpoints, and then selecting another midpoint. I tried it with varying segment counts and it worked every time. Here it is:
-
-
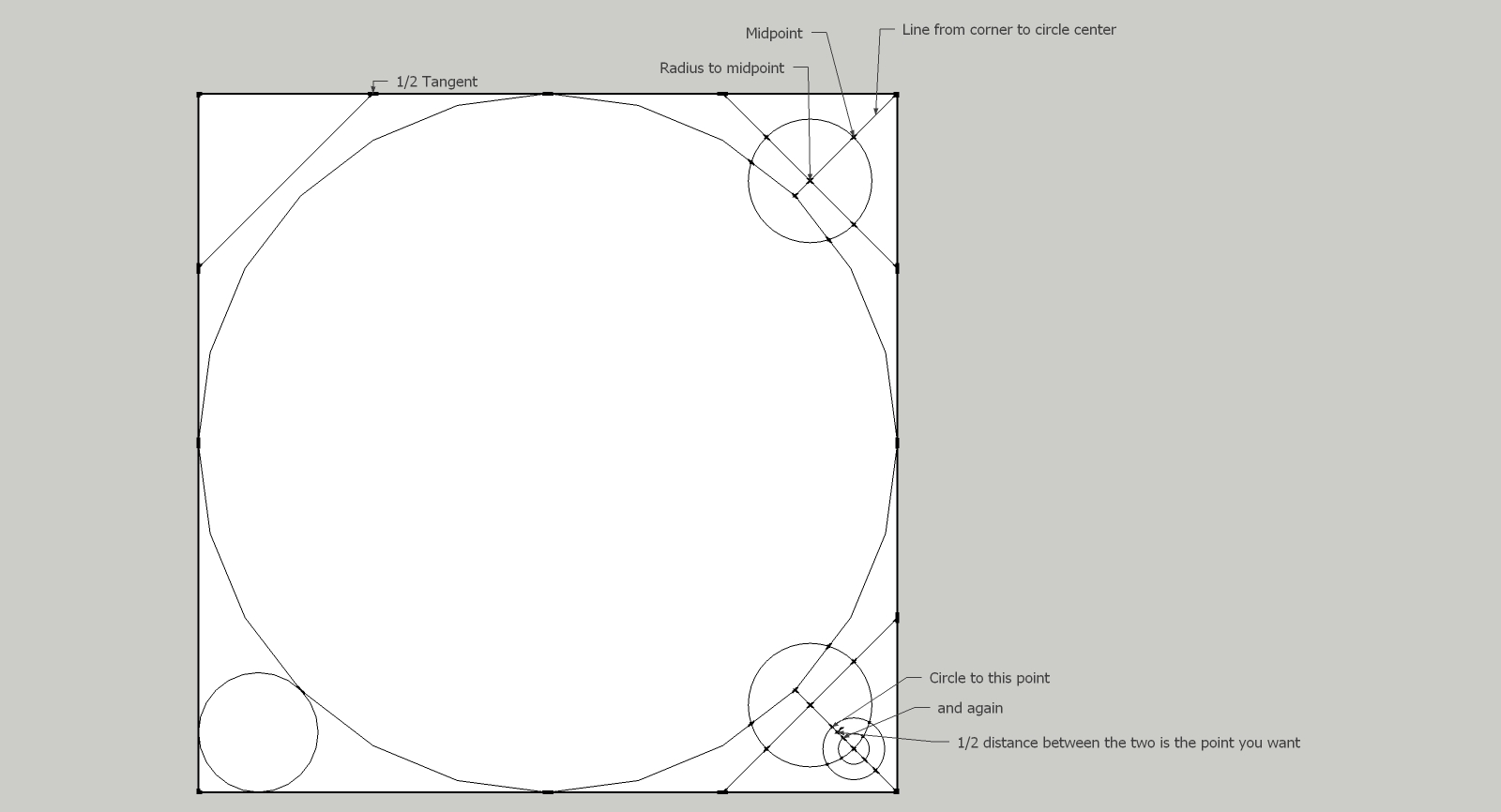
@jean lemire said:
Hi folks.
See this SU file for ideas:
Perfect!
Thank you! That helped a lot. Everything is much clearer now. Also, d12dozr, interesting plugin. I'll try it out sometime. 
-
catmando
A tip.
I cannot open Jena's post since still on 7 so hope this is not a repeat
"They" had a compass also.
Consider this: You can inscribe a circle in a triangle by bisecting its angles and this will give the circles center.( Jean has a very creative way to do this. (Rotate one side to other and then /2). For the corner case this makes it very easy. For the smaller ones the question is where are the tangents points unless you want to make your model with many segments. In either case remember there are no real tangents in SU ( have not looked at TIG's true tangent plugin however). The reason I say this is the definition of a tangent is: " The limit of line through points 1 and 2 on a curve as point 2 approaches point 1". For SU you will get two different answers ( ie different line slopes ) as you approach a vertex from one direction vs another and therefore tangent does not exist.
-
Hi folks.
V7 added in my previous post.
Best regards.
-
Jean thanks
Old school really helps.
I see getting second circle with triangle only problematic in finding the tangent points -
@mac1 said:
..... For SU you will get two different answers ( ie different line slopes ) as you approach a vertex from one direction vs another and therefore tangent does not exist.
For informative purpose see attached file.
The "real" tangent in a vertex of the segmented arc in SU is easy to find.
Rotate/copying one segment_extention towards the other segment and then apply dividing technique ( type /2 [Enter] ).
Zoom in on the vertex through scene 1->5. Each subsequent smaller arc is created on a "parent" larger segment by the magenta tangent arc.I'm not quite sure if your answer contradicts this tangent technique so.... the model is for informative purpose.
Thanks Jean for your excelent solution.
-
@Wo3Dan:
Your skp is in version 8, even though your profile says you use version 7. I attempted to download and found this out. -
-
Believe me, sir. Stupid is not a word I would associate with you. You help so many here.
-
Hey guys! Just stopping by and sharing how the third circle came to be:
You can probably trace what I did here... I was following Jean Lemire's guide (thank you very much for that, by the way!) and found a pretty simple method. I drew the tangent of the first circle you suggested I use and then drew a line from the radius of the second circle off to the right along the red axis. I found the radius of the third circle was exactly one-half the radius of the second, so I made a line of that distance and aligned it to the green axis at the point where the tangent and the radius-line-thingy met. The other end of that line was the center of the circle, and from there I drew the shape.
That may be unclear, and if so, I apologize... I didn't bother to label the lines or anything. The only thing that bothers me is that the first and third circles don't exactly meet up, but it's understandable considering they're all using under 40 sides. It's not very noticeable from afar anyway.
Advertisement