According to the doc, it should be 3D Catmull interpolation. I will test.

Hi Thomas

@unknownuser said:

The Catmull-Clark based subdivision that OpenSubdiv uses does cause shrinking. There are no options to have it lie on the surface of the control mesh

***As I mentioned initially, I like the concept of SubD a lot.
From my point of view it delivers a major missing functionality in Sketchup:

• Model and work with low poly producing a small file size
• When needed, with the press of a button, switch all components between the low and a high poly version back and forth as often as you want.
  Simply great!***

Therefore my question: Would you consider extending the SubD plugin to provide an additional option "CatMull-Interpolation" (as opposed to the existing CatMull-Clark approximation that shrinks)?
(Remark: In technical design and architecture, objects like walls should not shrink in a high poly version)

I did some tests using the BZ-spline plugin (from Fredo6) offering a CatMull curve Interpolation.
The results are in attached pictures. It shows, that the CatMull interpolation yields the same results as the SubD CatMull-Clark SubDiv algorithm, just that it does not shrink the object and all vertices are on the subdivided Surface.
What I did is basically use the two top and bottom loops ("circles") and generated a CatMull interpolation using the plugin. (It added a middle point outside each edge). Then I manually connected all new edges to get the quads for the subdiveded cone.

The original cone with slanted chopped head:

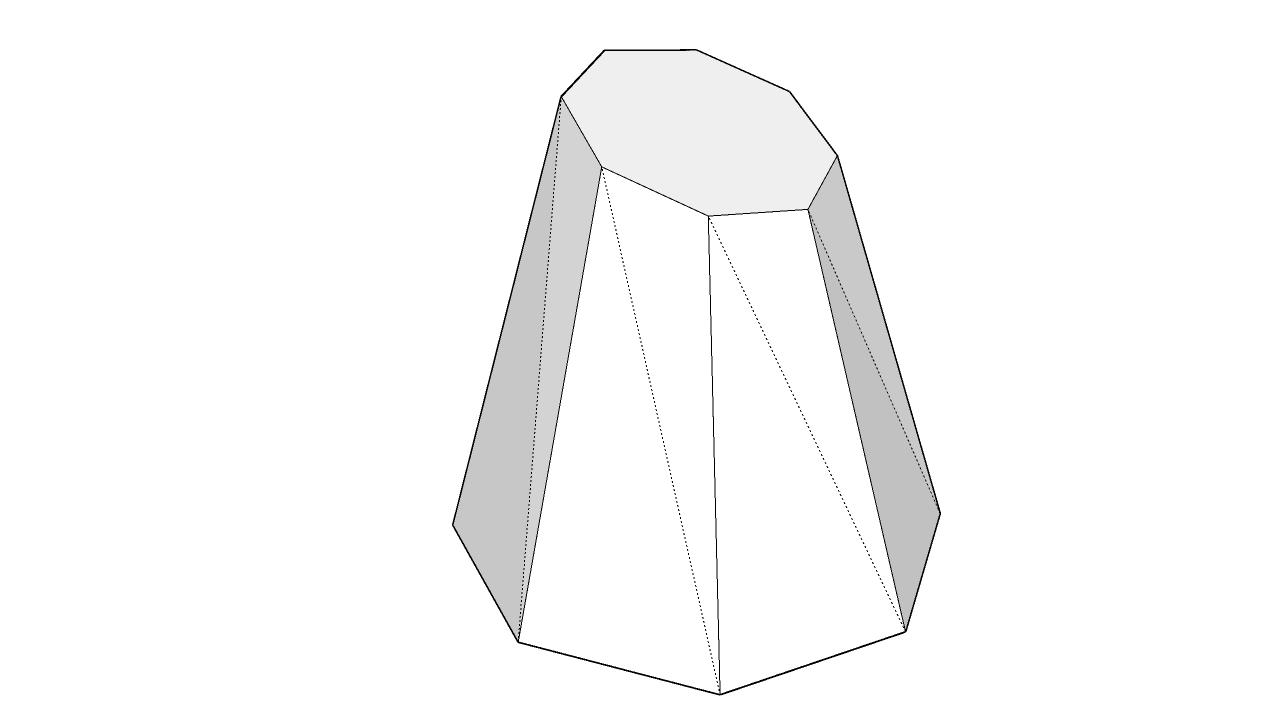
Subdivided cone with SubD level 1. The wire-diagram of the original cone shows the "shrinking":

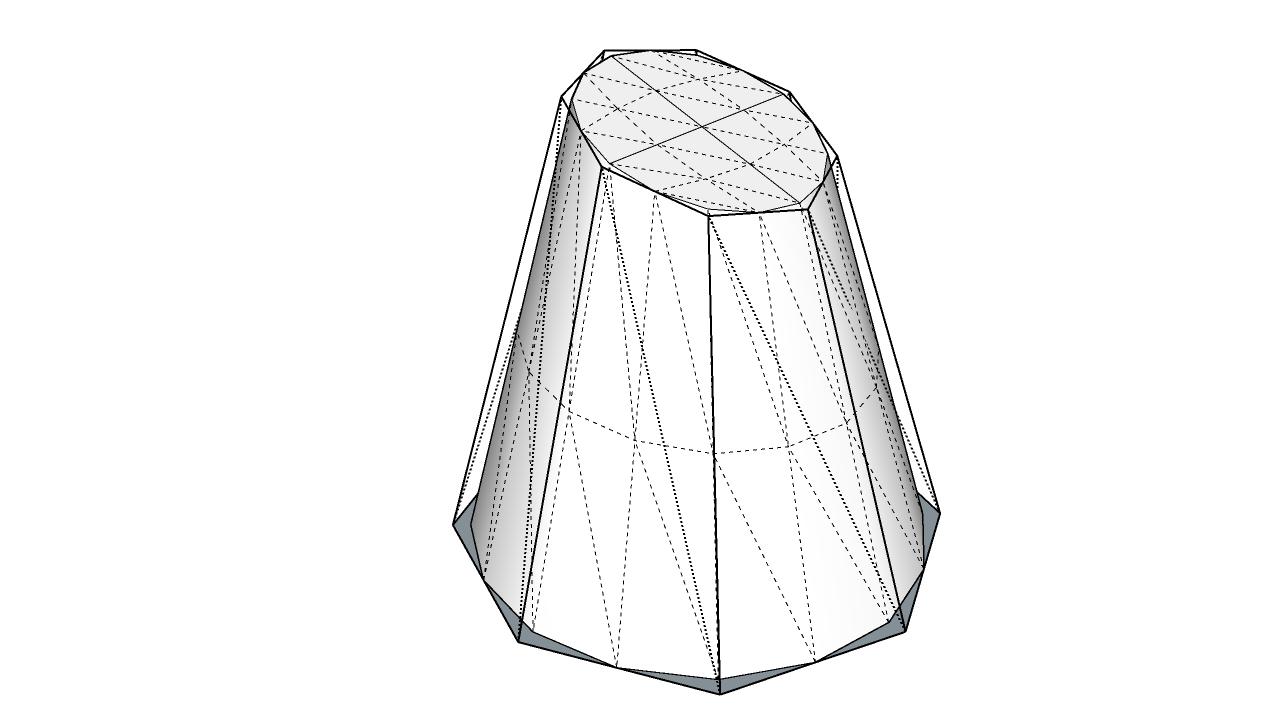
Manually subdivided cone using CatMull curve interpolation (added 1 point for each edge) and the wire diagram of the original cone:

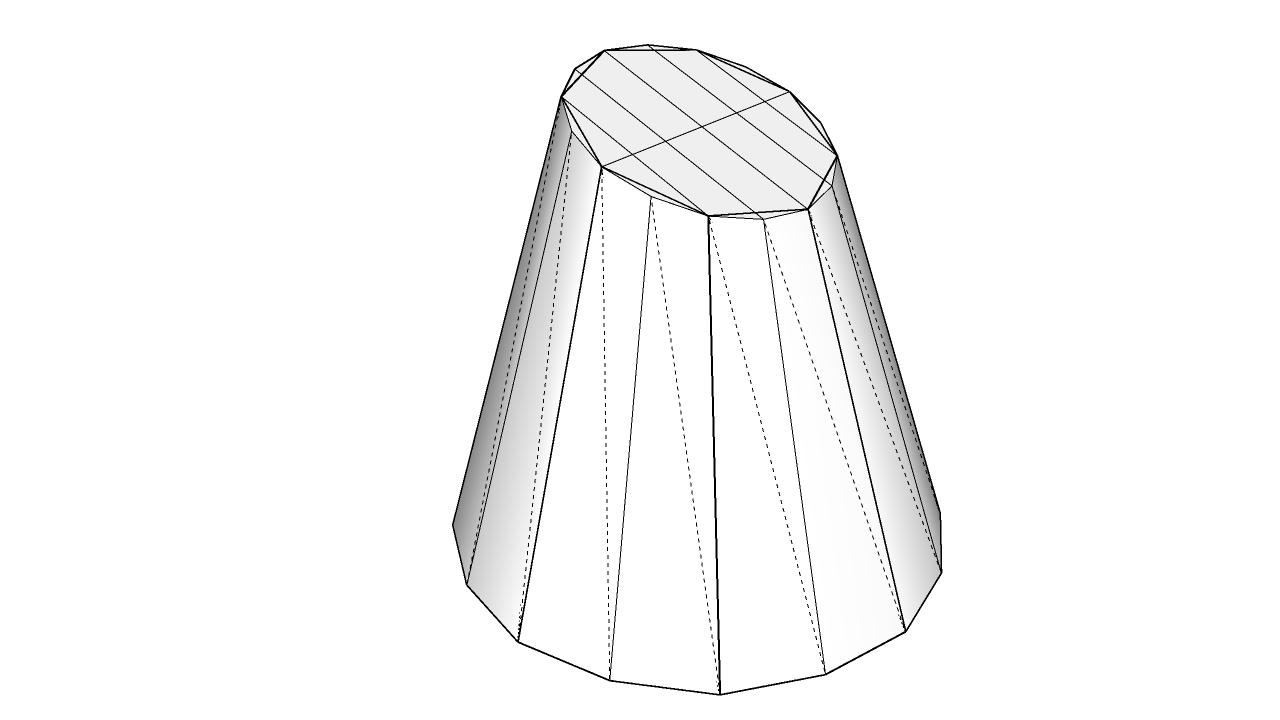
Manually vs SubD subdivided Cone. SubD Version has the same shape, just a bit smaller:

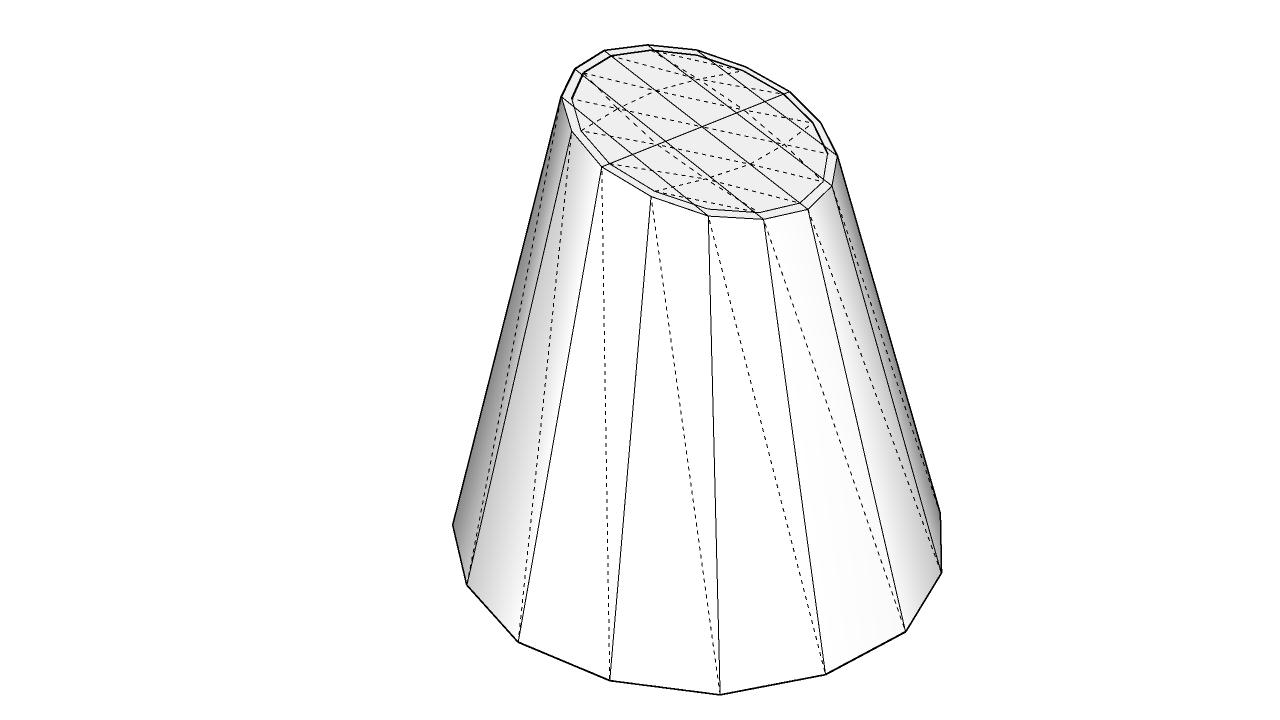
The example I did does not cover subdividing in all three dimensions (it would be a lot of manual work), but I hope it shows the idea.

Best Regards
Uwe

Agree, crease will keep the point in place, but the sub-divided surface is then not a sphere anymore. I would like both.

Hi Thom

here a screenshot of the original and subdivided mesh:

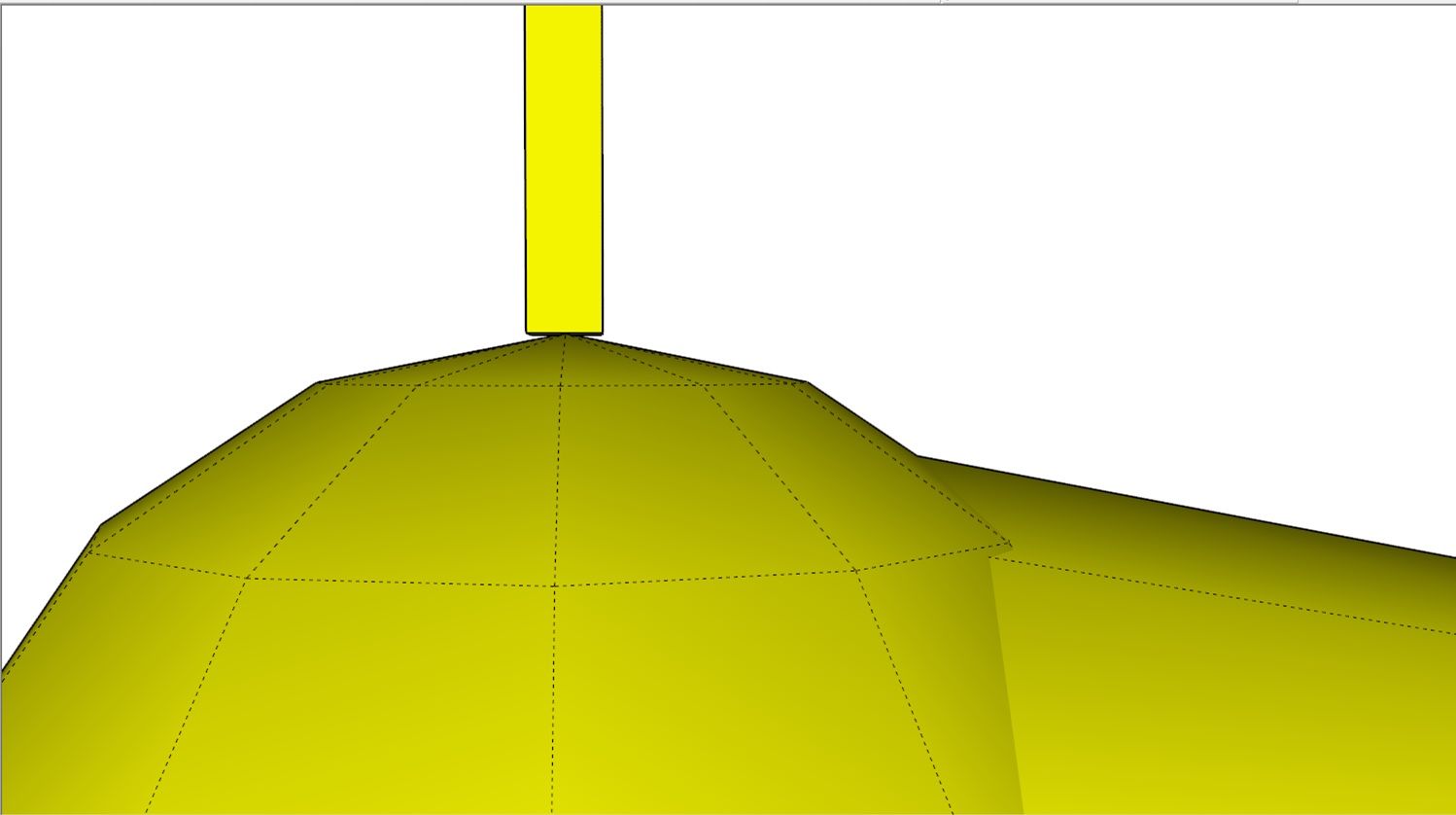
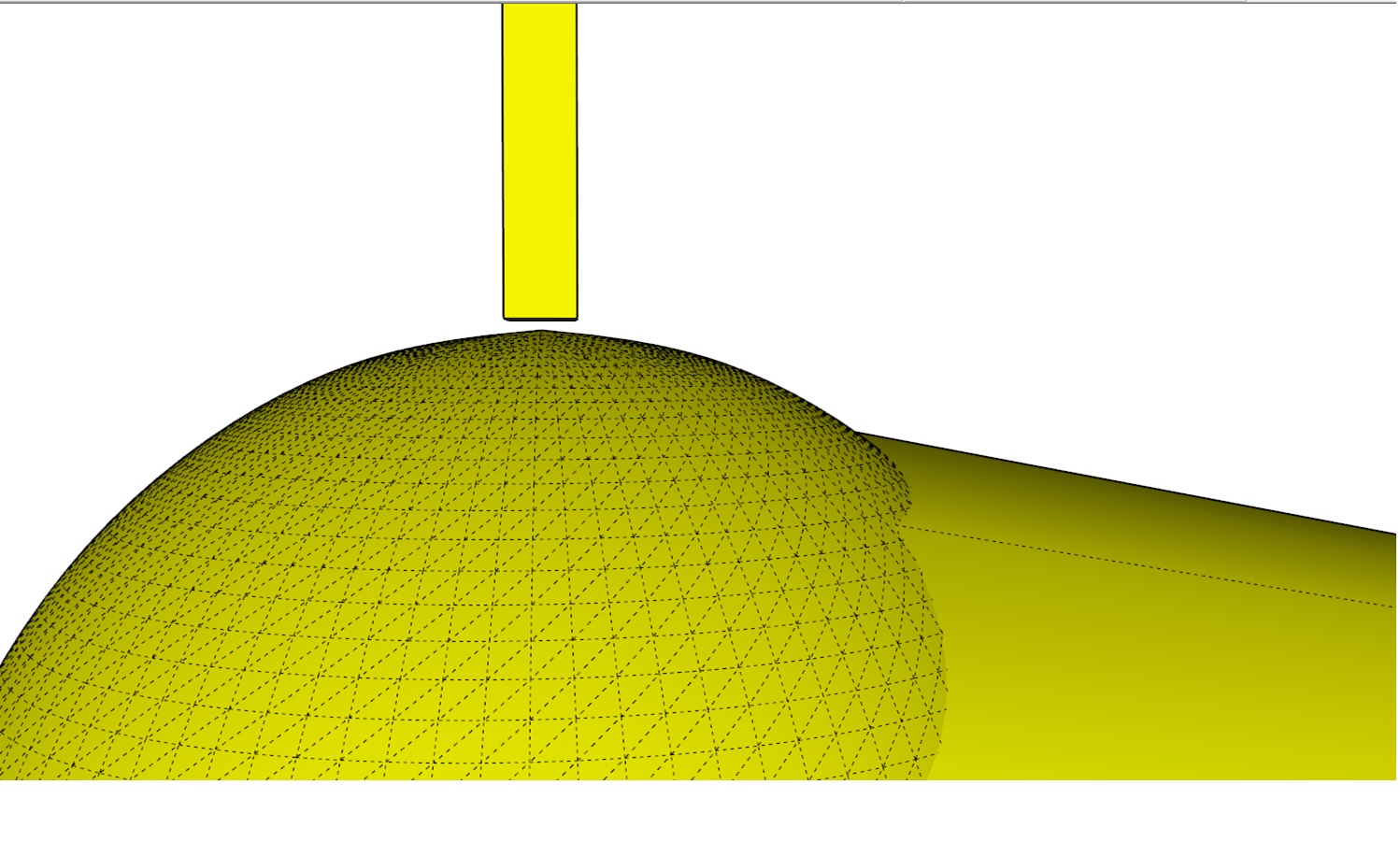
Maybe SubD could check where the mesh touches other components and then preserve the location of these points. Or the points to be kept on the surface could be defined by the user like the "crease edges" are defined.

I realized, that when in above example placing the touch point on the sphere on a very small plane, that then the sphere is not shrinked at that point (the blue line touches the surface before and after sub-dividing).
Could such a plane be added programmatically to avoid shrinking at a point?

Screenshot of the "chopped" sphere before and after sub-dividing:

![Original "chopped" mesh](/uploads/imported_attachments/98vC_Original_chopped_Mesh.jpg "Original "chopped" mesh")

![Subdivided "chopped" mesh](/uploads/imported_attachments/Ueos_SubDivided_chopped_Mesh.jpg "Subdivided "chopped" mesh")

Hi,

I model obejcts with low poly count and use SubD to create a nice looking Version. This is perfect for models with a large number of components - The high poly components can be generated on the fly when needed with one command.

Now I have some components that are by design touching each other at a point. But SubD shrinks the objects when sub-dividing and then the components are not close to each other anymore.
How can I avoid this shrinking? Or can SubD "inflate" them in the end, so that the points in the original mesh are on the surface of the sub-divided mesh (only the points, not the edges)?

Kind Regards
Uwe

Hi

Rounding an edge excluding the corners generates the arc as connected segments, not a curve/arc.
is it possible that along edges an arc/curve is generated?
That would help a lot in technical drawings where I need to know the radius of the rounding arc.
The corners are generated perfectly.