Mini-Challenge #2
-
Yes the are an infinity of quadrangles!
If you make the inverse, Draw the rectangle on view top
You can draw any number of little triangle at the end of the rectangle
A anywhere on the left for have possibility to draw a triangleThen extend this little triangle and draw 2 big sides
Take a longer smaller than the end of rectangle so a constraint
Take a another longer smaller than the end of rectangle on the other side so a constraint again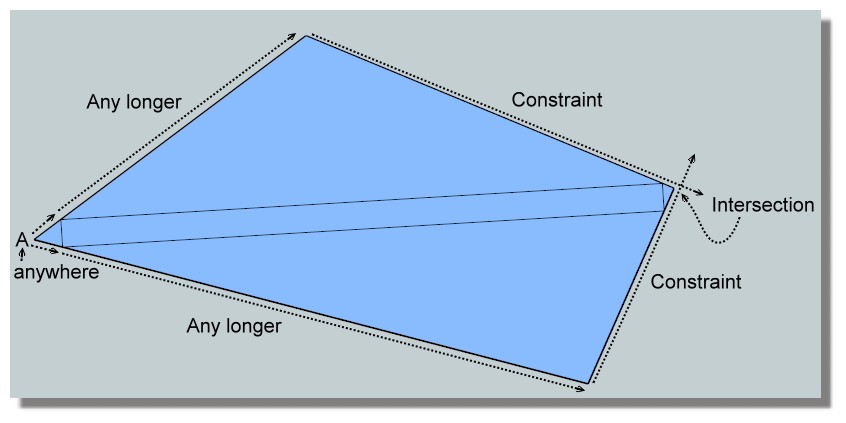
-
Yes Frenchy, in general. But I took Jeff's challenge to mean that all sides and angles of the quadrilateral were fixed and known. I think you can get from here to there using the cosine rule and some algebra, but banging my head against the possibility of a purely geometric, non-trig solution first.
-
@slbaumgartner said:
but banging my head against the possibility of a purely geometric, non-trig solution first.
don't bang tooo hard

fwiw, I saw this question at a rhino forum:
http://discourse.mcneel.com/t/geometry-riddle/14342at first, I thought it was going to be do-able via geometry but since then, a few very smart people have commented in the thread and/or posted solutions-- all of which seem iterative by nature (in some sense-- trial&error)
nobody has proven that a more simple (straight-forward) geometric approach isn't possible so that's why there's still a shred of hope but again-- don't bang your head too hard.
@frenchy-- yeah, doing it backwards (start with the 'board' and draw the 'room' around it) has infinite solutions.. (it also shows that an infinite number of gons can work. (4,5,6,etc) sided shapes can be drawn around the rectangle.
the question is the other way though.. start with a known shape and bisect it with a rectangle.(also-- units aren't important.. can be any unit and doesn't need to be imperial)
-
For shapes with an odd number of corners more info is necessary, as there is no innate definition of "opposite corner".
-
@slbaumgartner said:
For shapes with an odd number of corners more info is necessary, as there is no innate definition of "opposite corner".
right- once you've come up with a method, more info would be needed in the case of odd or multi numbered corners.. though i think the initial problem boils down to 'fit a rectangle between two angles".. the number of sides is irrelevant..

-
@jeff hammond said:
@slbaumgartner said:
For shapes with an odd number of corners more info is necessary, as there is no innate definition of "opposite corner".
right- once you've come up with a method, more info would be needed in the case of odd or multi numbered corners.. though i think the initial problem boils down to 'fit a rectangle between two angles".. the number of sides is irrelevant..
[attachment=0:qfxswsu7]<!-- ia0 -->Untitled.jpg<!-- ia0 -->[/attachment:qfxswsu7]
Right, but when you eliminate the full shape you have to provide more info to pin down the problem. You can move and rotate either corner without changing its angle!
-
ok
-
You need to know several things...
The distance between the two points where the angles are located [the line forming one diagonal of the quad']
You also need to know the four angles subtended to that line by each of the four lines forming the two angles.
From that you can do some calculations to give the range of x/y sizes for the potential rectangles that will touch all four lines [aka the sides of the quad'].
And i assume that no one quad' internal angle can be >180 deg ?
Does a rectangle that touches a side at the vertex itself 'in the limit', also 'count' ?
-
@tig said:
Does a rectangle that touches a side at the vertex itself 'count' ?
i suppose there are a few cases where a corner of the rectangle would coincide with a vertex of the quad (it would be the point at which if the angles were offset any further, that particular quad wouldn't have a solution at all.. not all quadrangles will be solvable)
for all intents and purposes, the .skp in the original post has an unsolved shape in which all the things which need to be known are known.. so, using that one as an example, can you find a solution for it?
-
@jeff hammond said:
has an unsolved shape in which all the things which need to be known are known.. so,
There could be hidden unknowns or maybe known unknowns, perhaps even unknown unknowns that we either do or don't, may or may not, have known about whether we know about not knowing about them or not.
-

-
@box said:
@jeff hammond said:
has an unsolved shape in which all the things which need to be known are known.. so,
There could be hidden unknowns or maybe known unknowns, perhaps even unknown unknowns that we either do or don't, may or may not, have known about whether we know about not knowing about them or not.
I don't know about that...
-
Who knows ?
...
Someone does...

-
From TIG's drawing
There are 6 constraints A1, A2, B1, B2, distance A-B and "thickness" of the inscribed rectangle
Thus we need, twice, a 7*7 matrix to solve each of the two corners (A-B). Who can define them?The solution must give the distance (radius of the tangent circle) between the axe of the inscribed rectangle and each point (A and B).
-
http://youtu.be/_0TY6HHL25Y
A graphical solution. -
@sdmitch said:
A graphical solution.
hey sdmitch..
that's only doing one side of it though.. the difficulty comes when trying to fit the rectangle between two corners.
do you have a solution for that? -
@jeff hammond said:
@sdmitch said:
A graphical solution.
hey sdmitch..
that's only doing one side of it though.. the difficulty comes when trying to fit the rectangle between two corners.
do you have a solution for that?You have to repeat the process on the other end also of course. Connecting those lines to create a face produces a slightly skewed rectangle. Rotating the ends to create a regular rectangle moves the ends but, in my test, by less than 0.01" from the edge. The perfect solution would require several iterations.
-
Each of the two corners have two extreme limits.
Where the 'x' width of the inscribed rectangle's end meet at 90 degrees.
These limits have an 'overlap' at each end.
If the corner's angle is <=90 degrees then the possible range is limited.
if is the 'overlap' of the two possible solutions.
If its > 90 degrees the range is 'x' set off from the corner vertex itself [of course only the full range applies if the quads angles are 90 degrees]
You only need to test one 'corner'.
You take a series of pairs of points which fall within the two 'overlap' zones on the two edges sharing that corner's vertex - which of course must also be exactly 'x' apart when measured at the angle.
of an inscribed rectangle.
To do that we need to project a line from the two end vertices, at a vector that is transformed to be perpendicular to that line [x], and check if it intersects with the lines of the other two edges [i.e. those which are not shared the 'corner']; and where it does, if that intersected point is between the two ends of the tested line, and then of the length of the two tested vectors from each of the x.vertex.position to the hit.point is the same length, then the two long sides of the rectangle would be corrected so we have a match.
To minimize the number of tests the two corners could be compared and the overlap lengths compared - the shortest set then have the fewest tests...
Now potentially there is a whole series of solutions for 'x' in the minimum corner's zone set that would fit an inscribed rectangle into the quad...
Now to code it... -
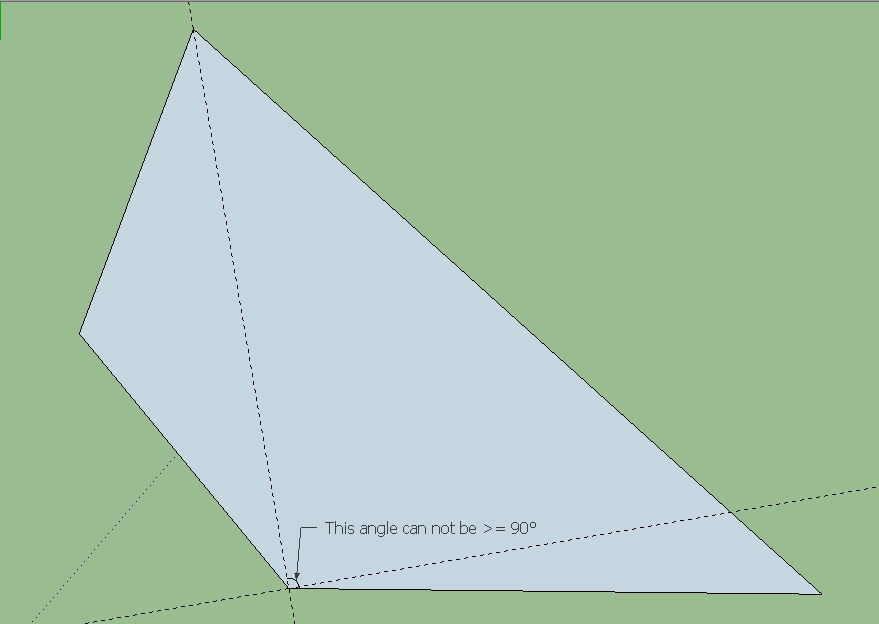
I worked out an analytic geometry solution using the formulas for the distance between two points and for the intersection point of two given lines. Solving is "just" a matter of algebra. However, the remaining difficulty is that the math formulation covers various configurations that have no real-value solution (e.g. attached image) and it is difficult (or at least confusing) to weed these out of the formulas.

-
@slbaumgartner said:
I worked out an analytic geometry solution using the formulas for the distance between two points and for the intersection point of two given lines. Solving is "just" a matter of algebra. However, the remaining difficulty is that the math formulation covers various configurations that have no real-value solution (e.g. attached image) and it is difficult (or at least confusing) to weed these out of the formulas.
[attachment=1:2acewcov]<!-- ia1 -->Screen Shot 2014-12-02 at 9.43.20 AM.png<!-- ia1 -->[/attachment:2acewcov]
Advertisement







