Drop Geometry to Surface - Brainstorming for methods
-
Dropping an object by insertion point or by bottom bounds corner is easy enough.
But do anyone have ideas for how to drop an object by it's vertices?
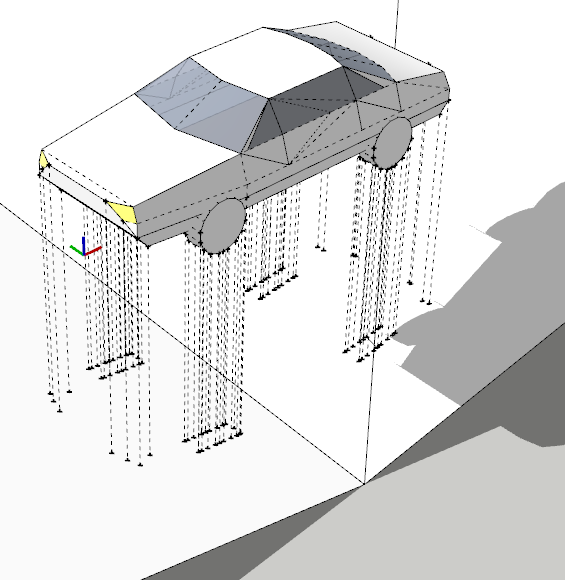
I'm able to find the points facing the surface underneath - but then what?
Any clever way of fitting the object to the surface? -
I'm not sure I understand what you want to do. Is the object a ComponentInstance?
-
SmartDrop does this, so maybe there are some ideas to be drawn out from it.
-
@jim said:
SmartDrop does this, so maybe there are some ideas to be drawn out from it.
SmartDrop deals with the bounding box of the instances - not the actual geometry.
-
@martinrinehart said:
I'm not sure I understand what you want to do. Is the object a ComponentInstance?
Drop a
GrouporComponentInstancedownwards to the surface underneath by the actual geometry inside. -
An instance will 'rest' on the surface on three points [?].
Test all instance-vertices and their intersections with the surface - getting paired points.
Take the pair with the shortest distance between them.
We'll all that instance_pt0 and surface_pt0
Drop the instance vertically onto that surface-point.
Now retest [excluding the instance_pt0, that is now zero distance away].
If at least two of the other tested vertex-points are also zero distance away you do nothing more as the instance now rests on the surface.
If not then find the nearest matched pair again = instance_pt1 and surface_pt1.
This time you can't 'drop' the instance - you need to rotate it in 3D so this second vertex is touching the surface NEAR surface_pt1 [can actually be on it!].
To do that find the
angle = surface_pt0.vector_to(surface_pt1)angle_between(surface_pt0.vector_to(instance_pt1))
then the transformation to rotate the instance
axis = surface_pt0.vector_to(surface_pt1).cross(surface_pt0.vector_to(instance_pt1)) tr = Geom::Transformation.rotation(surface_pt0, axis, -angle) ### it's untested! or maybe +angle ??? instance.transform!(tr)
Now we have the instance rotated so that instance_pt0 and instance_pt1 both touch the surface...
Retest for nearest matched pair again - this time omitting the 2 vertices that touch the surface.
If there is at least one pair at zero distance do no more since you have three touching vertices; if not you need to re-rotate the instance again so that the third [nearest paired] vertex instance_pt2 again touches the surface NEAR the intersection at surface_pt2.
We need a pivot_point relative to surface_pt0 and surface_pt1...
vector01=surface_pt0.vector_to(surface_pt1) line01=[surface_pt0, vector01]
Find the point on line01 nearest surface_pt2
pivot_point = surface_pt2.project_to_line(line01)
Find the vectors from pivot_point to surface_pt2 and instance_pt2 and the angle between them
etctetcyawn!
'cross' the vectoro1 and the vector pivot_point.vector_to(surface_pt2) to get the rotation_axis.
again transform rotation the instance about pivot_point and rotation_axis by ang [or -ang???] and you should now have at least 3 points of contact ?????????????
I ran out of steam during the last few bits of code but you get the idea...........
-
That's the thing - is brute force the only method? Testing all kinds of combinations?
Another issue: say you find three points that rest of the surface, now, it could be that they are very close together - say a chair's leg, you might end up with the chair resting on one foot and the remaining three legs in the air.
I guess we are then talking about taking mass and gravity into account - a whole lot more complicated?One way I was pondering about was - brute force iterate over various combinations and see in which combination the most points are closest to the surface ... ?
-
not really sure how krill is doing this but maybe it's related?
http://forums.sketchucation.com/viewtopic.php?t=24676
.
-
@unknownuser said:
not really sure how krill is doing this but maybe it's related?
http://forums.sketchucation.com/viewtopic.php?t=24676
.
Never noticed that plugin before.
It's not doing what I'm trying to do though - but still interesting. It subdivides the selected group and makes it fit to the surface underneath. Nearly like vacuum forming. Could come in handy. -
@thomthom said:
I'm able to find the points facing the surface underneath - but then what?
Any clever way of fitting the object to the surface?There's a theread over at GG, where a guy and I discussed this a few days ago.
He had a different purpose of course.
contour seen from above
. -
Maybe kirill2008 Stick groups to mesh can inspire
http://forums.sketchucation.com/viewtopic.php?t=24676 -
@notareal said:
Maybe kirill2008 Stick groups to mesh can inspire
http://forums.sketchucation.com/viewtopic.php?t=24676Same as Jeff's link.

Advertisement







