Logic with arcs (mini-challenge?)
-
fwiw, the drawing in the above post isn't correct but it shows that infinite solutions are available.. if you zoom in on the arcs' intersection you'll see they don't touch.. at this point, using the method i normally do i would have to make very small moves with the arc divided in 250 or so segments (ie - moves of say 27/512" until i get it super close then redraw the arcs and fix the seam.. it never ends up exact.. the one in the top post is exact but i didn't draw it while using constraint -- i move the boxes into place after the arc were drawn)
-
Damm, just when i thought i was getting a grasp on the thing shakes fist
-
i thought about this a little more and i came up with a way to simplify it (well simplify thinking about it.. not solving it)
the only reason there's an infinite number of solutions is because i'm letting one of the radii vary.. (and actually, it would be better for me if i choose the arcs because it's a lot easier on the jobsite to have a 7-9 radius than one at 7-8 37/64..)
so yeah, both of the arcs are pre-determined (let's say the right one is 12' and the left one is 10') the box on the right can still slide left/right and finding it's position is actually The X factor.
now there's only one answer
-
i just downloaded turbocad to try this in and it's super easy.. one of the circle drawing options does exactly this..
just drew the arc on the left then clicked the circle tool at which point i'm prompted to enter the diameter of the other arc.. after that, click on the left arc then click on the bottom line of the rectangle and it's done..
i realize SU's arcs are segmented but i really only need a couple of guide points (one where the arcs touch and one where the right arc is tangent to the line (bottom edge of the right box)
i'm sure it's rubyable and i might propose this as a ruby challenge if this thread doesn't pan out.. with prizes and everything
 (but i'm not putting up more than twenty bucks for the prize
(but i'm not putting up more than twenty bucks for the prize  )
) -
i'm gonna see what TIG thinks about it:
http://forums.sketchucation.com/viewtopic.php?p=191749#p191749
don't tell him about the twenty though

-
@unknownuser said:
[EDIT - read through the thread a bit because one of the variables in the drawing has been omitted.. there is now only one variable and one solution]
here's a situation i'm faced with on occasion and while i'm usually ok with using geometry inside SU to achieve solutions, this one has me stumped.. i have a method of doing this but it takes way too long (trial and error) and i'm almost positive there's a solution using sketchup tools that i've overlooked.
i hope the attached skp shows the situation clearly.. (and no 'kinda close' methods
 .. i can do that easily.. it has to be precise)
.. i can do that easily.. it has to be precise)you'll see there are two items that are predetermined -- the rectangle on the left and the arc's radius on the right (though the length of this arc can vary)... two items are variable (the left/right orientation of the rectangle on the right and the arc's radius/length on the left)
[attachment=2:2vukwdnz]<!-- ia2 -->arcsQuestion.jpg<!-- ia2 -->[/attachment:2vukwdnz]the winner will receive everything he/she has ever hoped for in life!
The old problem of reverse curve through two lines and a secant line. Do not agree there is only one solution. You can rotate the given radius around x degs , a perdendicular than establishes the secat line and tangent point and then arcs can be drawn
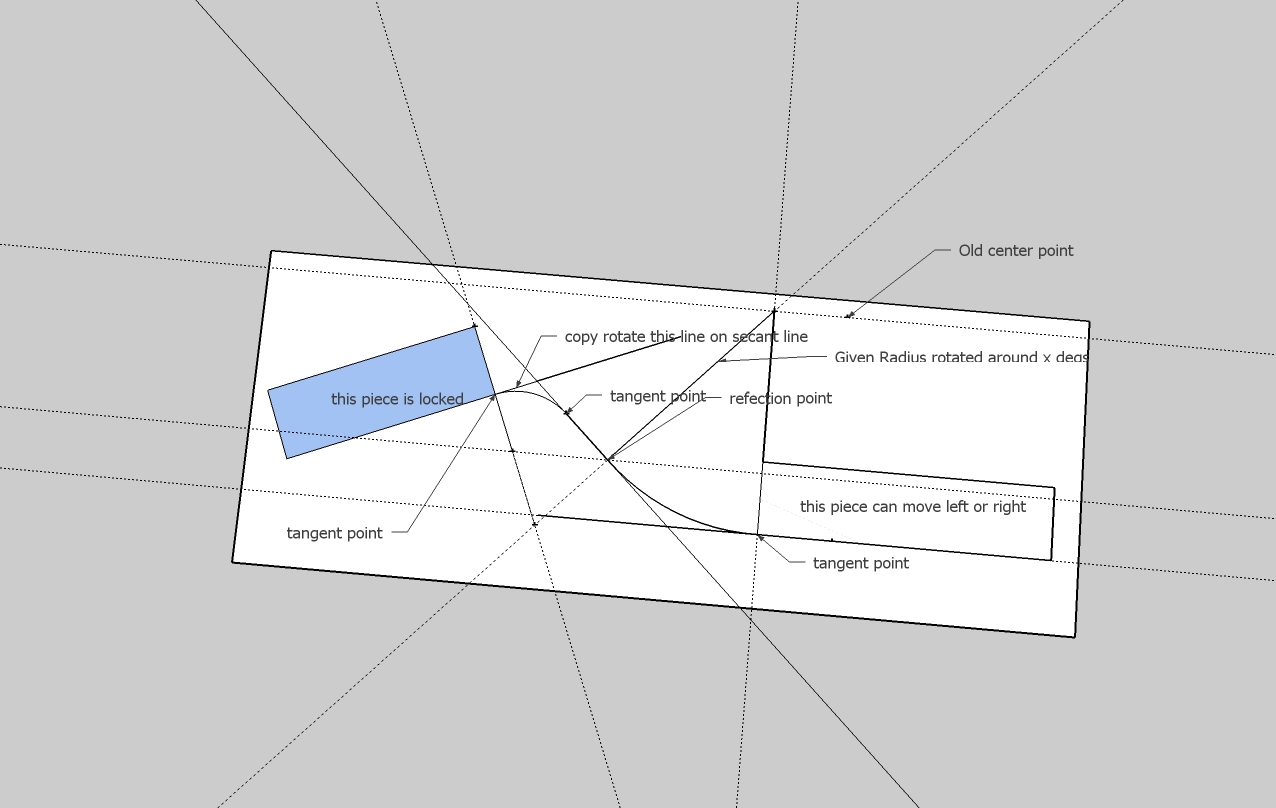
-

yes! thank you! feel free to claim your prize

not sure if this is exactly what you're suggesting but it's the same principal.. again, thanks for helping
[Edit] -- ok, i see what you did and the result is different (with the flat spot in there) but good thing.. i build stuff like that too..
[flash=640,385:21uku9q1]http://www.youtube.com/v/eMOGUaVsyDg&hl=en&fs=1&rel=0&color1=0x2b405b&color2=0x6b8ab6[/flash:21uku9q1] -
Jeff,
Geometry is just mathematics with constraints or extra rules if you will. You cannot solve a problem unless you have enough known variab les. In Geometry this also means you cannot solve by starting with a piece of geometry that is not locked down. Your sliding right hand box is an example. You have to start with the left.
You can make the problem easier if you define the tangent radii as equal. Since you want 12'6" for the initial I'd make them both 12' 6"
In the old days on a drafting board I would have done this with just a compass, dividers, and a straight edge.

The attached SKP shows the process step by step. I used 96 segments per Arc to make things smoother.
-
[oops.. post messed up.. i'll retype and repost

-
@unknownuser said:
:shock:
yes! thank you! feel free to claim your prize

not sure if this is exactly what you're suggesting but it's the same principal.. again, thanks for helping
[Edit] -- ok, i see what you did and the result is different (with the flat spot in there) but good thing.. i build stuff like that too..
[flash=640,385:2mbqv38e]http://www.youtube.com/v/eMOGUaVsyDg&hl=en&fs=1&rel=0&color1=0x2b405b&color2=0x6b8ab6[/flash:2mbqv38e]The flat spot is just a straight line connecting the two arcs and depending on the specific geometry you may or not get that
-
@mac1 said:
The flat spot is just a straight line connecting the two arcs and depending on the specific geometry you may or not get that
right.. like in the video, i could of made a much tighter radius on the right by using a flat spot.
still, i'm definitely satisfied with the solution
-
@gruff said:
Geometry is just mathematics with constraints or extra rules if you will. You cannot solve a problem unless you have enough known variab les. In Geometry this also means you cannot solve by starting with a piece of geometry that is not locked down. Your sliding right hand box is an example. You have to start with the left.
right, i get what you're saying and i think the sliding box isn't the best way to pose the question.. i asked TIG if he can update his TrueTangets ruby to deal with this and i think the question was presented a little better to him [see jpg at the bottom of this post]
anyway, the problem is more to do with the fact that arcs are segmented in sketchup instead of round.. i can draw this on the job site at full scale using basically a giant compass and since i'm working with round edges, it makes it a lot easier.. since the lines aren't really round, i had to abandon my other methods and find a way to get the arc centerpoints without using their edges.. mac1 definitely came through there..
@unknownuser said:
You can make the problem easier if you define the tangent radii as equal. Since you want 12'6" for the initial I'd make them both 12' 6"
maybe. but that's not really a solution i'm after.. in this exact circumstance, 12'6 is way too loose for the finished product to be functional..
@unknownuser said:
In the old days on a drafting board I would have done this with just a compass, dividers, and a straight edge.

The attached SKP shows the process step by step. I used 96 segments per Arc to make things smoother.
thanks for taking the time to draw this up.. it does however show the problem i'm talking about with the segmented arcs.. if you zoom in, you'll notice the arcs aren't really tangent and they're overlapping.. that's the degree of accuracy i've been working with in the past in this situation but i made this thread to get truly accurate..
here's the question posed a little differently: (towards the end of pg2 in the thread)
http://forums.sketchucation.com/viewtopic.php?f=180&t=19457that's really the ultimate solution for me because i could then very easily and quickly get the exact two radii i want to use.. until then, the method shown in the video of this thread will do just fine..
[question as presented to TIG for a ruby solution]

-
hey gruff.. your method does in fact work out to be accurate if you divide some of the arcs into 500 or so segments.. and actually, that's a really nice way to see it.. i like it .. i think it'd be better to do in layout or something that draws true arcs because snapping to intersections would be easier than hyper-divided segmented arcs in SU.
so cool, 2 different approaches now!
[hoping TIG adds the 3rd and final
 ]
] -
@gruff said:
Of course they also had filleting (Corner Curves) which could easily solve your problem in one step. All could create a fillet between two lines, arc and line, or two arcs.
In your case it would be between the left arc and the horizontal line at the bottom right.that's the ruby request to TIG in the picture above.. the idea came from a cad program.
@unknownuser said:
All that said I wonder about your need for accuracy in this case. In the real world everything has a tolerance and not suprisingly when you start to build things over 6 to 10 feet your measuring tools start to throw their own errors into the mix.
For instance how accruate do you think a tape measure is? Sag, flex, temperature, material and other factors add to the issue. This is why in building construction an error of 1/8 inch is an everyday occurance.the need for accuracy is more to do with adjoining pieces in SU rather than real world.. if i draw a piece that's almost correct and butt it with a piece that is correct, i end up with holes in surfaces that are basically impossible to fix.. so i have to draw the incorrect piece first and copy/move it around the drawing for the next few weeks and draw everything else with the same error just so the finished drawing will line up.. 1/128" errors in SU are the biggest pain because for one, they're very hard to detect and usually even harder to fix..
i know it's possible to draw it very accurately and easily so why not strive to do so?
as to real world tolerances, i deal with them everyday and it's no big deal.. tapes have errors sure.. or 7' on one tape isn't the same 7' on the other.. the lumber i work with can vary by 1/4" thickness etc.. foundations with dips in them.. moisture expansion/contraction working differently on the separate types of materials i use.. all of it.
that said, i definitely try not to compound the errors.. a small error on top of another small one can add up to something bigger than the sum of the two.. surely you can understand this and i think you'd agree that it's not the smartest thing in the world to make a bad drawing just because you know there will be some +/- on the site..
anyway -- i've finally arrived at a method for doing the drawing to 100% accuracy while being able to choose the radius of both arcs.. it's pretty simple to do and a definite hand/head moment considering how many times i've fought this in the past.. i'll draw up a little tut in a bit for anyone interested..
(btw, i build skateboard ramps if you're wondering what these curves are for.. there are 3-4 situations i use these convex/concave tangents for.. this ramp shows two of those situations)

-
For anyone interested, i'm attaching a tutorial showing how i'll be doing this from now on. (well, unless TIG adds it to TrueTangents
 )
)fwiw, it's a mismash of methods suggested by mac1 and gruff in this thread.. thanks dudes.
-
http://forums.sketchucation.com/viewtopic.php?p=160780#p160780 'filletarc' now added.
Adds radiused fillet helpers to a selected arc/circle and line/cline to a radius given in a dialog...
-
http://forums.sketchucation.com/viewtopic.php?p=192769#p192769 'tangentialarcs'
Doesn't quite do what your tutorial shows... it makes the tangential arcs from the arc/line selected... I'll do another version that is more a 'fillet' arc to line tool - you select an arc and a line, the tool asks for a radius in a dialog and it creates the center/tangent-points etc need to construct the arc fillet to suit... Watch this space...
-
Jeff,
I can see the faceting of curves in Sketchup as being a big issue. It is to me as well.
My background is mechanical engineering and I have used many different CAD systems over the years. All of them used true arc and circles so this was never an issue.Of course they also had filleting (Corner Curves) which could easily solve your problem in one step. All could create a fillet between two lines, arc and line, or two arcs.
In your case it would be between the left arc and the horizontal line at the bottom right.All that said I wonder about your need for accuracy in this case. In the real world everything has a tolerance and not suprisingly when you start to build things over 6 to 10 feet your measuring tools start to throw their own errors into the mix.
For instance how accruate do you think a tape measure is? Sag, flex, temperature, material and other factors add to the issue. This is why in building construction an error of 1/8 inch is an everyday occurance.Aerospace is the only industry I know of that has addressed the problem with any success.
They are starting to use a new technology called indoor GPS.
This uses infraRed lasers mounted around the ceiling with the receiver in a hand held measuring tool. The user takes hits on the object to be measured and the 3D coordinate data gathered is uploaded and overlaid on the original CAD model. Boeing developed it.
Advertisement







