That's great modeling, but even more, it shows incredible anatomical knowledge and artistic sense.

Very nice engineering and design. I especially like the subtle wood grain.

I'll bet using SU to replicate the Sun at various times of year and day was real useful. I assume the screen is on the west side to keep from blinding the guests.

Here are some detail shots from the full version of the model/plan.

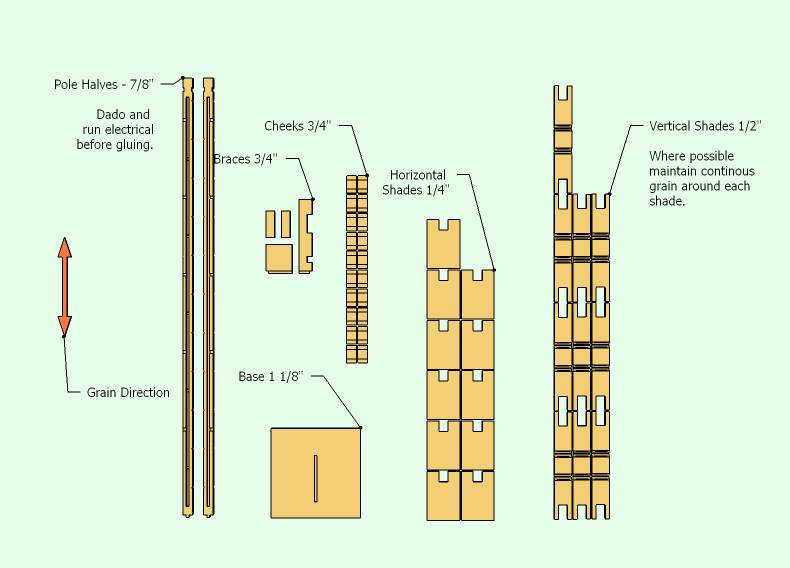
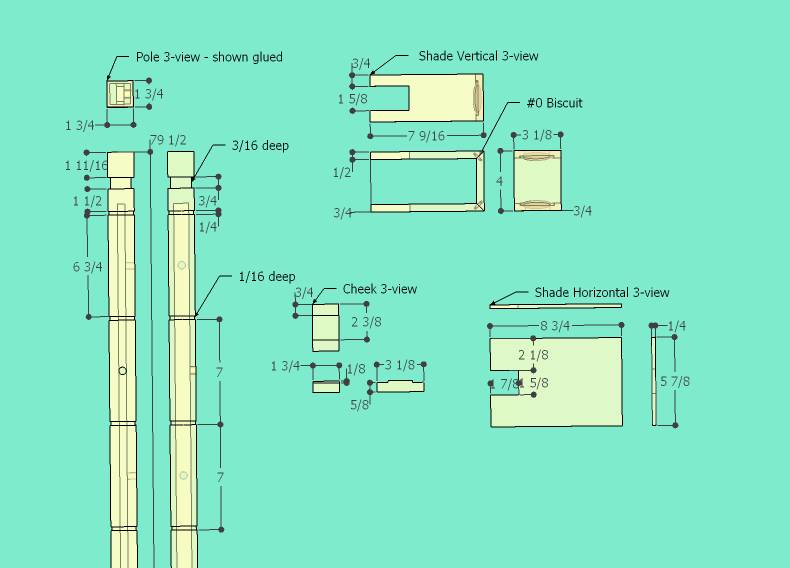
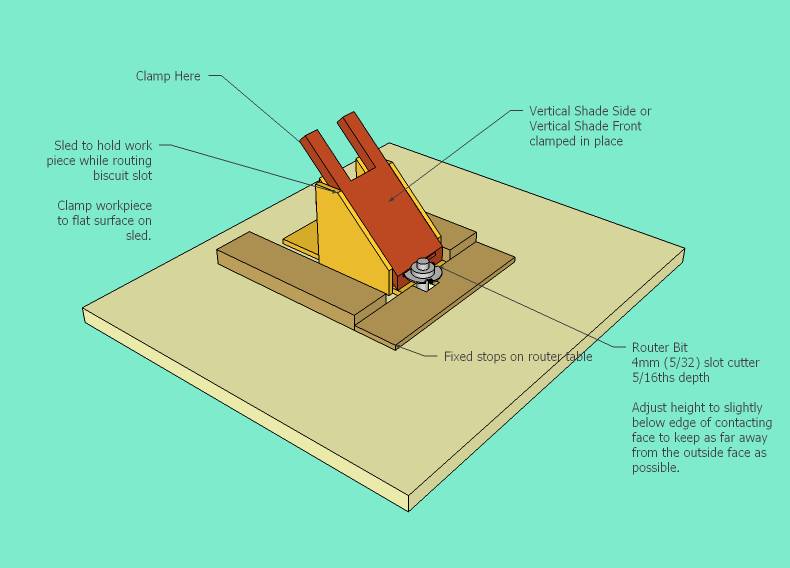
The fully detailed model is here: http://sketchup.google.com/3dwarehouse/details?mid=18809736617cbe7e4326824bb7387d70

I made a model of this floor lamp in detail as a working plan. Here are a couple of simplified versions that could be used as components.

The "ON" version is an attempt to show what the light would look like in the dark, turned on, just using SU materials. Sorta works, but not really.
http://sketchup.google.com/3dwarehouse/details?mid=ff479dddbb48197aea61e619272daaca

http://sketchup.google.com/3dwarehouse/details?mid=5abda7d039ec115b72349ee87c19f053

Honestly, the Taliesin 2, which is a floor lamp doesn't appeal to me nearly as much as the Taliesin 3 which is a desk lamp. I hope to make one of those too.

They look good Tom. You are way ahead of me in Kerkythea. I tried it a few times just recently and got frustrated. When I have time, I hope to play more.

A beautiful picture.

My only concern is that the boat to starboard should let the mainsheet out a bit or it could have an unexpected jibe.

That is so good. I especially like the light coming through the curtains. The bits which jump out at me are the jackets, they look too similar and too perfect - and the cord for the speaker doesn't look quite right - too thick, two uniform, I'm not sure?

When price is no object, there is usually a solution, but here the geometry doesn't leave much room to work. My first thought was searchlights shining outward from where you want to sit, so that anyone looking your way would be blinded. A more realistic possibility would be walls or at least trellises on the sides of the supports for the deck. With a southern exposure, that would afford a place for someone to expose themselves to the sun if that is the goal.

Not that it will help, but here is a mathematical proof that pi is irrational:

Quote:
Niven's proof

The proof uses the characterization of π as the the smallest positive zero of the sine function. Like all proofs of irrationality, the argument proceeds by reductio ad absurdum.

Preparation: Suppose that π is rational, i.e. π = a / b for some integers a and b ≠ 0, which may be taken without loss of generality to be positive. Given any positive integer n, we define the polynomial function

f(x) = {x^n(a - bx)^n \over n!},\quad x\in\mathbb{R},

and denote by

F(x) = f(x) + \cdots + (-1)^j f^{(2j)}(x) + \cdots + (-1)^n f^{(2n)}(x). ,

the alternating sum of f and its first n even derivatives.

Claim 1: F(0) = F(π)

Proof: Since

f(x)=b^n{x^n(\pi - x)^n \over n!}=f(\pi-x),\quad x\in\mathbb{R},

the chain rule and mathematical induction imply

f^{(j)}(x) = (-1)^j f^{(j)}(\pi - x),\quad x\in\mathbb{R},

for all the derivatives, in particular

f^{(2j)}(0)=f^{(2j)}(\pi),

for j = 1, 2, ...,n and Claim 1 follows from the definition of F.

Claim 2: F(0) is an integer.

Proof: Using the binomial formula to expand (a – bx)n and the index transformation j = k + n, we get the representation

f(x)={1\over n!}\sum_{j=n}^{2n}{n \choose j-n}a^{2n-j}(-b)^{j-n}x^{j}.,

Since the coefficients of x0, x1, ..., xn − 1 are zero and the degree of the polynomial f is at most 2n, we have f (j)(0) = 0 for j < n and j > 2n. Furthermore,

f^{(j)}(0)={j!\over n!}{n \choose j-n}a^{2n-j}(-b)^{j-n}\quad\mbox{for } n\le j\le 2n.

Since j ≥ n, the fraction of the two factorials is an integer. The same holds for the binomial coefficient, as can be seen from its combinatorical interpretation or Pascal's triangle. Hence f and every derivative of f at 0 is an integer and so is F(0).

Claim 3:

\frac12 \int_0^\pi f(x)\sin(x),dx=F(0)

Proof: Since f (2n + 2) is the zero polynomial, we have

F'' + F = f.,

The derivatives of the sine and cosine function are given by (sin x)' = cos x and (cos x)' = −sin x, hence the product rule implies

(F'\cdot\sin - F\cdot\cos)' = f\cdot\sin.

By the fundamental theorem of calculus

\frac12 \int_0^\pi f(x)\sin(x),dx= \frac12 \bigl(F'(x)\sin x - F(x)\cos x\bigr)\Big|_{x=0}^{x=\pi}.

Since sin 0 = sin π = 0 and cos 0 = –cos π = 1 (here we use the abovementioned characterization of π as a zero of the sine function), Claim 3 follows from Claim 1.

Conclusion: Since f(x) > 0 and sin x > 0 for 0 < x < π (because π is the smallest positive zero of the sine function), Claims 1 and 3 show that F(0) is a positive integer. Since

x(\pi -x) = \Bigl(\frac\pi2\Bigr)^2-\Bigl(x-\frac\pi2\Bigr)^2\le\Bigl(\frac\pi2\Bigr)^2,\quad x\in\mathbb{R},

and 0 ≤ sin x ≤ 1 for 0 ≤ x ≤ π, we have

\frac12 \int_0^\pi f(x)\sin(x),dx\le \frac{b^n}{n!}\Bigl(\frac\pi2\Bigr)^{2n+1},

which is smaller than 1 for large n, hence F(0) < 1 by Claim 3 for these n. This is impossible for the positive integer F(0).

Not that I understand it, but there it is.

SchreiberBike

Masta Squidge wrote:
Please by all means message this joke to me! Unless its the one about the Special Olympics of course lol, because that is all too familiar.

Yep, that's the one.

SchreiberBike

There's a really good joke about the wisdom of arguing on the Internet, but it is not PC at all, so I won't post it.

I did once have a long series of respectful discussions about global warming and actually changed some people's minds. I find that pretty amazing.

SchreiberBike

Masta Squidge wrote:
He stated to me that since someone made it, that means it HAS to have an end.

Nobody made Pi or 1/3, they are ratios. Perhaps if he believes that God made the universe he will believe that God made those ratios. If God did it, perhaps he will believe that the ratios have no ending when expressed as numbers.

SchreiberBike

Any landing you can walk away from is a good landing.

Since no one was on board, I guess that was a good landing. The flight sure looked good for about two seconds.

SchreiberBike

I'll believe it when it really flies.

SchreiberBike

Granted. You are now a chartered yacht and rich families rent you to sail around the Caribbean.

I wish I could lose 7.2 billion dollars.

Everybody must try this at some point, but I thought it was my turn. My face in SU.

I'd like to live there.

SU is great for those ideas in the back of your head which want to see just a bit more reality.

Not a direct answer to your question, but I've thought about purchasing one of these:

for exactly that purpose. It's from http://www.woodcraft.com/family.aspx?FamilyID=20439.

Nice work. I especially like the reflected logo. The whole logo is very versatile.

Are folded cards common where you are? Very rare in the US.

I want to have a picture of a not-long deceased real person in a model.

Would it be legal/appropriate to use a number of photos and other pictures I remember for "inspiration" - then use new textures and lines and make a new image which doesn't have any of the original material to make a 2D person?