Simpler formula for central angle?
-
so i hacked this formula together but i'm feeling like it's too convoluted.. it works fine but is there a simpler way to find a central angle (circle) when the input is radius(r) & chord length(c)?
2*(ACOS((SQRT((r*r)-(.25*(c*c))))/r))that's a combination of this:
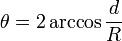
plus this for the d:
sqrt(radius*radius-(chord*chord*.25))i feel like i should be able to use one of these (used for finding chord length):
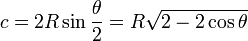
except i can't seem to get the chord and theta on opposite sides of the = and have it work out right

(also,is there a better way to type r^2 [instead of (r*r)] that will work in a dc formula?
thanks
-
Use the 'Sine Rule':
diameter = chord_length / sin(center_angle_subtended_to_chord_ends)
and of course...
radius = diameter / 2
or
radius = chord_length / (2 * sin(center_angle_subtended_to_chord_ends))
rearranging formula...
chord_length = diameter * sin(center_angle_subtended_to_chord_ends)
or
chord_length = radius * 2 * sin(center_angle_subtended_to_chord_ends)
and to find the angle...
center_angle_subtended_to_chord_ends = asin(chord_length / diameter)
or
center_angle_subtended_to_chord_ends = asin(chord_length / (radius * 2))
Using your variable naming
angle=asin(c/(r*2)) -
thanks Tig
(though i think that's for 1/2 the central angle.. but definitely what i was after.)
fwiw, here's a rough version of what i'm using it for..
it draws an arc with 3 different inputs -- radius, segment length, and # of segmentsselect the component then use the component options dialog
i don't necessarily see an immediate use for this because the arc segments are buried so deep.. i think when it i try to make a useful dc (such as that fillet example i posted the other day -- which i'm thinking is possible now), i'll just have it make guide points and i'll draw the arcs/lines over them..
-
It is the angle between the 2 radii at the 2 ends of the chord...
-
@tig said:
It is the angle between the 2 radii at the 2 ends of the chord...
Right. After reading your post a few times, I realized that I was looking at the whole thing wrong (way over thinking it
 )
)
Your post made me realize there's a right triangle (or 2) in there. Right triangles I can deal with ok.
Advertisement







