Logic with arcs (mini-challenge?)
-
[EDIT - read through the thread a bit because one of the variables in the drawing has been omitted.. there is now only one variable and one solution]
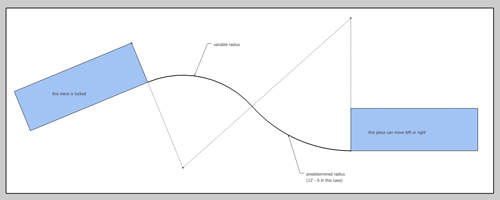
here's a situation i'm faced with on occasion and while i'm usually ok with using geometry inside SU to achieve solutions, this one has me stumped.. i have a method of doing this but it takes way too long (trial and error) and i'm almost positive there's a solution using sketchup tools that i've overlooked.
i hope the attached skp shows the situation clearly.. (and no 'kinda close' methods
 .. i can do that easily.. it has to be precise)
.. i can do that easily.. it has to be precise)you'll see there are two items that are predetermined -- the rectangle on the left and the arc's radius on the right (though the length of this arc can vary)... two items are variable (the left/right orientation of the rectangle on the right and the arc's radius/length on the left)
the winner will receive everything he/she has ever hoped for in life!
-
Hmmm, seems theres infinitely many solutions to the problem, not that that helps in solving it, of course.
-
@remus said:
Hmmm, seems theres infinitely many solutions to the problem, not that that helps un solving it, of course.
but ultimately, there's only one right answer to the situation which is why i think there must be a way to obtain this..
but yeah, there are many, many different ways to approach it but i've yet to come across THE ONE

-
I meant as in theres actually lots of different 'answers' you could get, all of which would satisfy your conditions. Might whip out the maths at some point and see if i can prove this

-
On second thoughts, is the circumference of the fixed radius arc fixed?
-
@remus said:
On second thoughts, is the circumference of the fixed radius arc fixed?
the length of the fixed radius arc can change..
still, you'll see there aren't a bunch of different answers to it.. there's only one. [edit - okay, i see what you're saying.. yes, there are many solutions]
(well, actually, there are plenty of different answers but i'm not giving all of the background.. the arc on the left is variable to an extent as is the the left/right orientation of the box on the right.. ) i don't think it's important to introduce those restrictions though in order to find a method to do this..
[for instance, the rectangle on the right is really only able to move say 1' in either direction and the left arc's radius needs to stay between 8' and 9'... within those restrictions though, there are still infinitely possibilities so let's not worry about placing restrictions on the variables]
-
dammed arrogance of youth, seems there is only one solution.
-
@remus said:
dammed arrogance of youth, seems there is only one solution.
haha, you're right.. that's how i saw it at first but then your posts changed my mind but now i'm back to my original thought.. there's only one answer.. the fact that the rectangle on the right can't move up/down means there's only one true solution..
there's a bunch of things happening and it's hard to remember all of them at once

[EDIT]
ok, i'm driving myself crazy now and i'm thinking too much here about the wrong things but there are infact infinite solutions..
-
fwiw, the drawing in the above post isn't correct but it shows that infinite solutions are available.. if you zoom in on the arcs' intersection you'll see they don't touch.. at this point, using the method i normally do i would have to make very small moves with the arc divided in 250 or so segments (ie - moves of say 27/512" until i get it super close then redraw the arcs and fix the seam.. it never ends up exact.. the one in the top post is exact but i didn't draw it while using constraint -- i move the boxes into place after the arc were drawn)
-
Damm, just when i thought i was getting a grasp on the thing shakes fist
-
i thought about this a little more and i came up with a way to simplify it (well simplify thinking about it.. not solving it)
the only reason there's an infinite number of solutions is because i'm letting one of the radii vary.. (and actually, it would be better for me if i choose the arcs because it's a lot easier on the jobsite to have a 7-9 radius than one at 7-8 37/64..)
so yeah, both of the arcs are pre-determined (let's say the right one is 12' and the left one is 10') the box on the right can still slide left/right and finding it's position is actually The X factor.
now there's only one answer
-
i just downloaded turbocad to try this in and it's super easy.. one of the circle drawing options does exactly this..
just drew the arc on the left then clicked the circle tool at which point i'm prompted to enter the diameter of the other arc.. after that, click on the left arc then click on the bottom line of the rectangle and it's done..
i realize SU's arcs are segmented but i really only need a couple of guide points (one where the arcs touch and one where the right arc is tangent to the line (bottom edge of the right box)
i'm sure it's rubyable and i might propose this as a ruby challenge if this thread doesn't pan out.. with prizes and everything
 (but i'm not putting up more than twenty bucks for the prize
(but i'm not putting up more than twenty bucks for the prize  )
) -
i'm gonna see what TIG thinks about it:
http://forums.sketchucation.com/viewtopic.php?p=191749#p191749
don't tell him about the twenty though

-
@unknownuser said:
[EDIT - read through the thread a bit because one of the variables in the drawing has been omitted.. there is now only one variable and one solution]
here's a situation i'm faced with on occasion and while i'm usually ok with using geometry inside SU to achieve solutions, this one has me stumped.. i have a method of doing this but it takes way too long (trial and error) and i'm almost positive there's a solution using sketchup tools that i've overlooked.
i hope the attached skp shows the situation clearly.. (and no 'kinda close' methods
 .. i can do that easily.. it has to be precise)
.. i can do that easily.. it has to be precise)you'll see there are two items that are predetermined -- the rectangle on the left and the arc's radius on the right (though the length of this arc can vary)... two items are variable (the left/right orientation of the rectangle on the right and the arc's radius/length on the left)
[attachment=2:2vukwdnz]<!-- ia2 -->arcsQuestion.jpg<!-- ia2 -->[/attachment:2vukwdnz]the winner will receive everything he/she has ever hoped for in life!
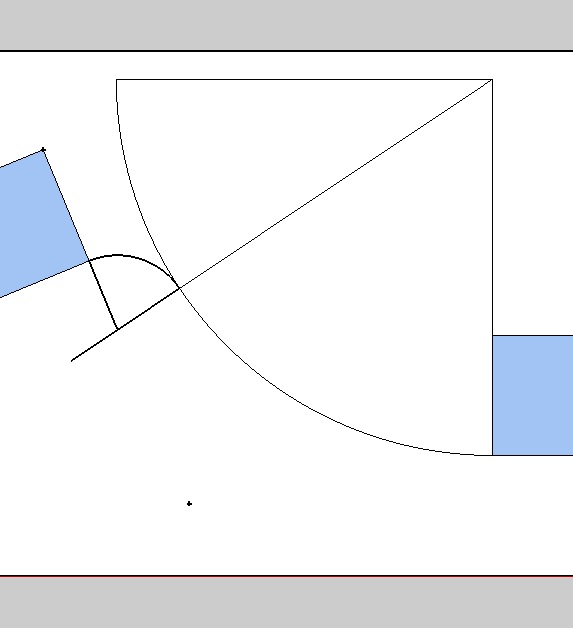
The old problem of reverse curve through two lines and a secant line. Do not agree there is only one solution. You can rotate the given radius around x degs , a perdendicular than establishes the secat line and tangent point and then arcs can be drawn
-

yes! thank you! feel free to claim your prize

not sure if this is exactly what you're suggesting but it's the same principal.. again, thanks for helping
[Edit] -- ok, i see what you did and the result is different (with the flat spot in there) but good thing.. i build stuff like that too..
[flash=640,385:21uku9q1]http://www.youtube.com/v/eMOGUaVsyDg&hl=en&fs=1&rel=0&color1=0x2b405b&color2=0x6b8ab6[/flash:21uku9q1] -
Jeff,
Geometry is just mathematics with constraints or extra rules if you will. You cannot solve a problem unless you have enough known variab les. In Geometry this also means you cannot solve by starting with a piece of geometry that is not locked down. Your sliding right hand box is an example. You have to start with the left.
You can make the problem easier if you define the tangent radii as equal. Since you want 12'6" for the initial I'd make them both 12' 6"
In the old days on a drafting board I would have done this with just a compass, dividers, and a straight edge.

The attached SKP shows the process step by step. I used 96 segments per Arc to make things smoother.
-
[oops.. post messed up.. i'll retype and repost

-
@unknownuser said:
:shock:
yes! thank you! feel free to claim your prize

not sure if this is exactly what you're suggesting but it's the same principal.. again, thanks for helping
[Edit] -- ok, i see what you did and the result is different (with the flat spot in there) but good thing.. i build stuff like that too..
[flash=640,385:2mbqv38e]http://www.youtube.com/v/eMOGUaVsyDg&hl=en&fs=1&rel=0&color1=0x2b405b&color2=0x6b8ab6[/flash:2mbqv38e]The flat spot is just a straight line connecting the two arcs and depending on the specific geometry you may or not get that
-
@mac1 said:
The flat spot is just a straight line connecting the two arcs and depending on the specific geometry you may or not get that
right.. like in the video, i could of made a much tighter radius on the right by using a flat spot.
still, i'm definitely satisfied with the solution
-
@gruff said:
Geometry is just mathematics with constraints or extra rules if you will. You cannot solve a problem unless you have enough known variab les. In Geometry this also means you cannot solve by starting with a piece of geometry that is not locked down. Your sliding right hand box is an example. You have to start with the left.
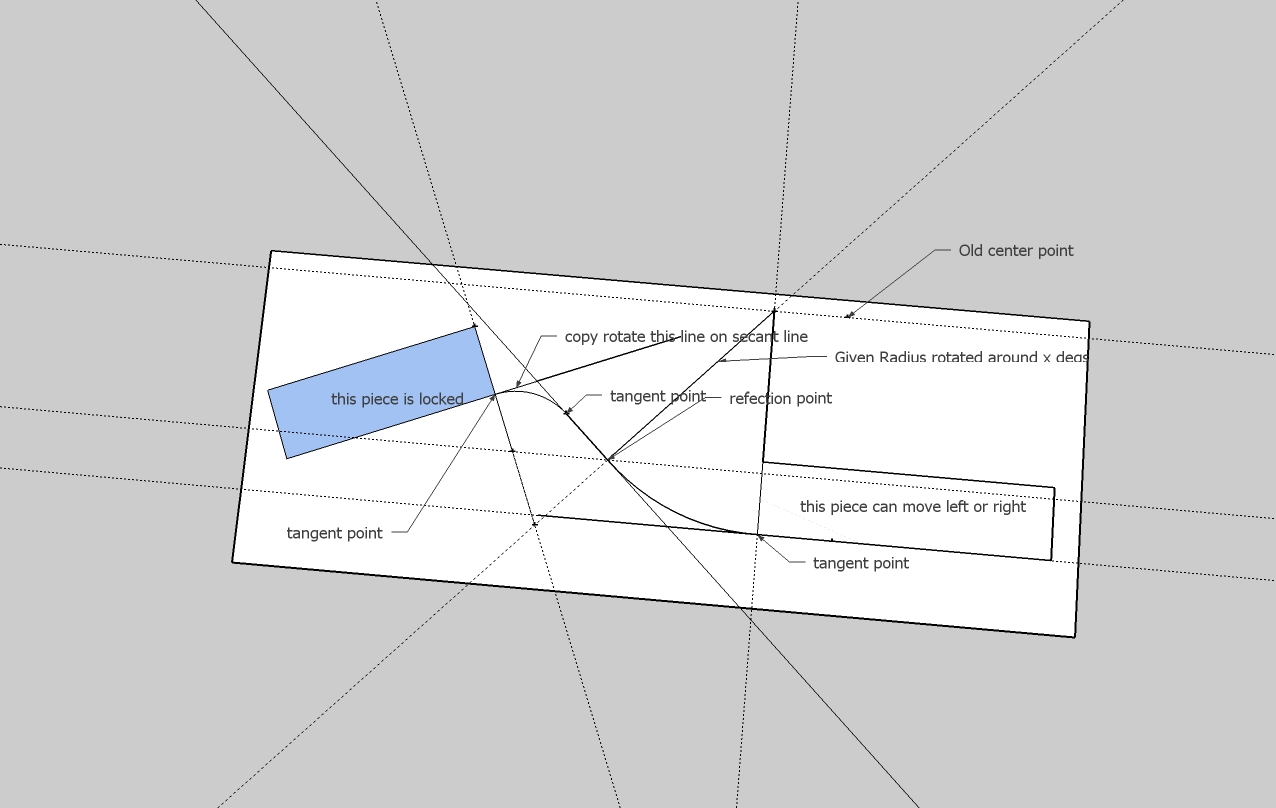
right, i get what you're saying and i think the sliding box isn't the best way to pose the question.. i asked TIG if he can update his TrueTangets ruby to deal with this and i think the question was presented a little better to him [see jpg at the bottom of this post]
anyway, the problem is more to do with the fact that arcs are segmented in sketchup instead of round.. i can draw this on the job site at full scale using basically a giant compass and since i'm working with round edges, it makes it a lot easier.. since the lines aren't really round, i had to abandon my other methods and find a way to get the arc centerpoints without using their edges.. mac1 definitely came through there..
@unknownuser said:
You can make the problem easier if you define the tangent radii as equal. Since you want 12'6" for the initial I'd make them both 12' 6"
maybe. but that's not really a solution i'm after.. in this exact circumstance, 12'6 is way too loose for the finished product to be functional..
@unknownuser said:
In the old days on a drafting board I would have done this with just a compass, dividers, and a straight edge.

The attached SKP shows the process step by step. I used 96 segments per Arc to make things smoother.
thanks for taking the time to draw this up.. it does however show the problem i'm talking about with the segmented arcs.. if you zoom in, you'll notice the arcs aren't really tangent and they're overlapping.. that's the degree of accuracy i've been working with in the past in this situation but i made this thread to get truly accurate..
here's the question posed a little differently: (towards the end of pg2 in the thread)
http://forums.sketchucation.com/viewtopic.php?f=180&t=19457that's really the ultimate solution for me because i could then very easily and quickly get the exact two radii i want to use.. until then, the method shown in the video of this thread will do just fine..
[question as presented to TIG for a ruby solution]

Advertisement







