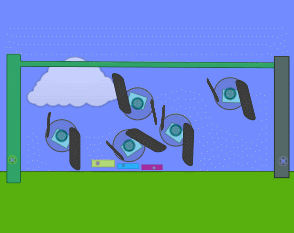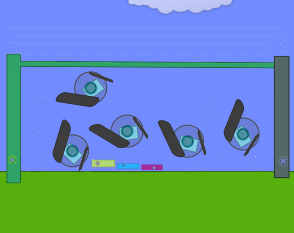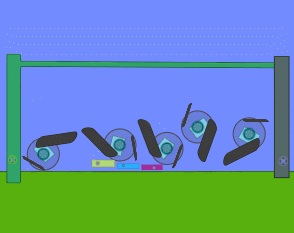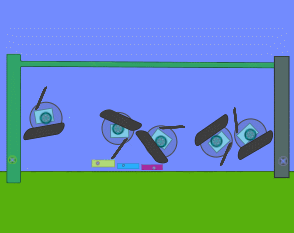
ROBOTIC LINKAGE MECHANISM simulator - ALGODOO - GEOGEBRA
-
-
Et comme c'est scriptable

-

-
@pilou said:
Et comme c'est scriptable

j'aurai pas du te chercher .

Très très belles démo
ALGODOO , ON SAIT QUAND ON COMMENCE .......
-
Comme on peut adresser les touches du claviers, on a la main sur les mouvements!

En dehors du fait bien sûr que pendant une animation on peut choper n'importe quoi à la souris en direct!
C'est le type même de programme générateur d'univers...plats!
bon là c'est pas lui, mais il fait tout ce qui montré!
-
C'est quand même un rien balèze!

-
Classique!

-
ça parait si facile

mais il doit falloir cogiter comme un malade!
-
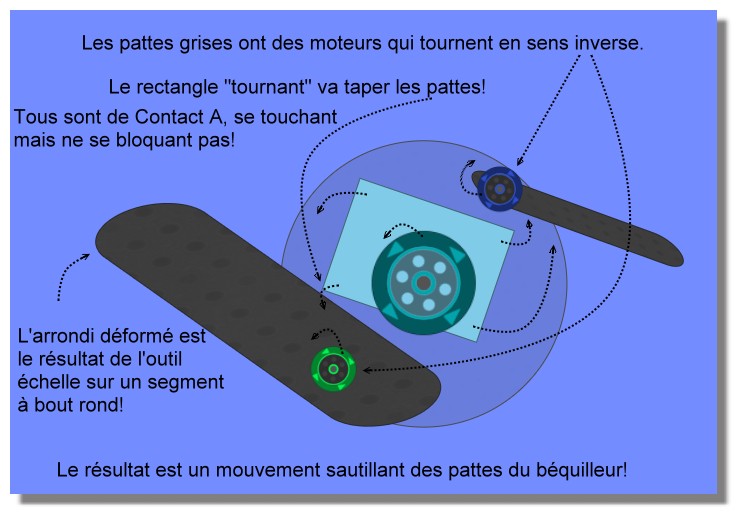
En effet! Il a du ressort le marcheur!

-
Juste un essai avec un fichier qui vient de sortir sur le forum

Faut cliquer! Âmes sensibles s'abstenir
Âmes sensibles s'abstenir 

-
-
Bonjour
Pour info , il est possible de télécharger des nombreux exemples ... a étudier.
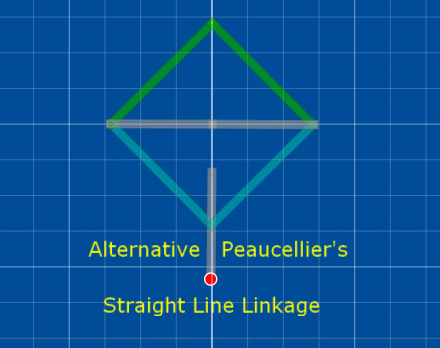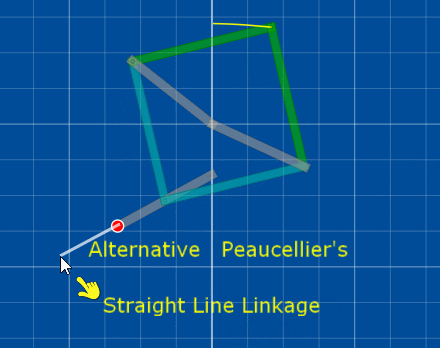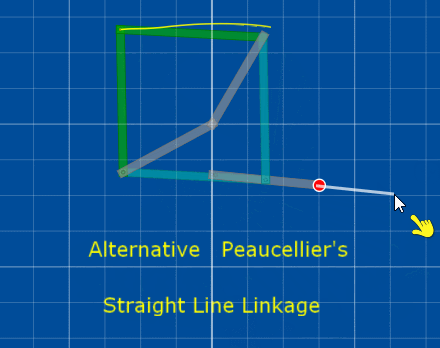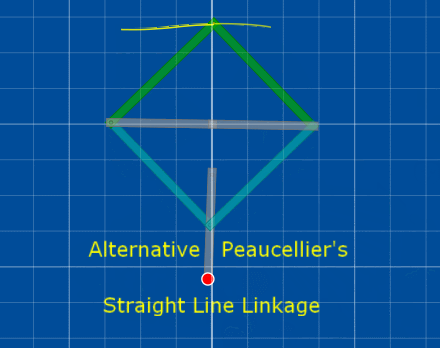
Celui que je viens de télécharger avec le mot clé LINKAGE est une simulation manuelle ( avec poignée de manœuvre )
[highlight=#ffff00:17vxgtpq]cliquer sur la 1ere image pour l'animer[/highlight:17vxgtpq]
Chri
a+
-
Nombreux exemples est un euphémisme : plus de 2 400 000 fichiers chargeables!

Oui pendant toute animation on peut continuer à faire tout ce qu'on veut!
Evidément comme cela bouge toujours c'est des fois très sportif si les choses ne sont pas fixées!
Heureusement qu'il y a la touche pause!
Il y a un truc très gadget, ce sont les palettes d'outils flottantes!

(à la MacIntosh même sur PC)
-
Etonnant non ?

-
Encore un autre!
Il a l'air d'avoir un autre concept d'animation! Minute O.42 !

-
Bonj
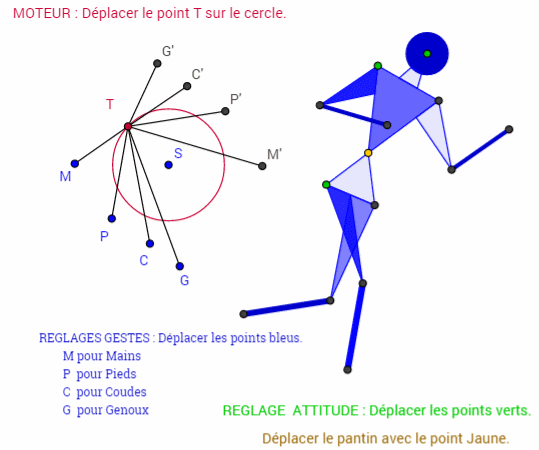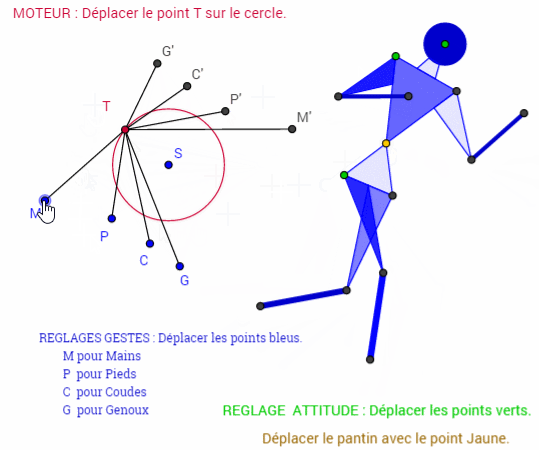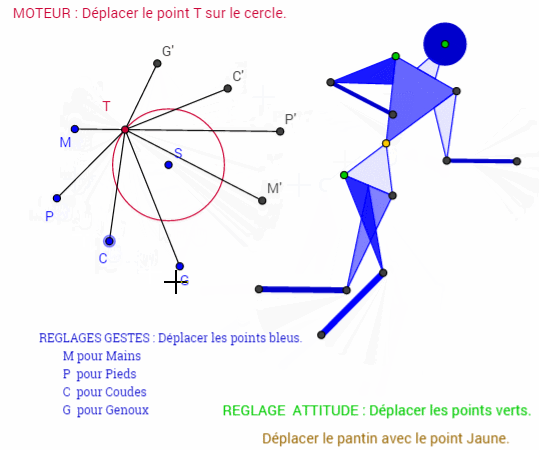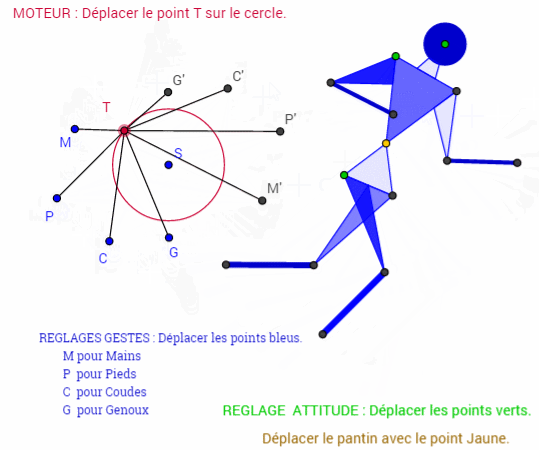
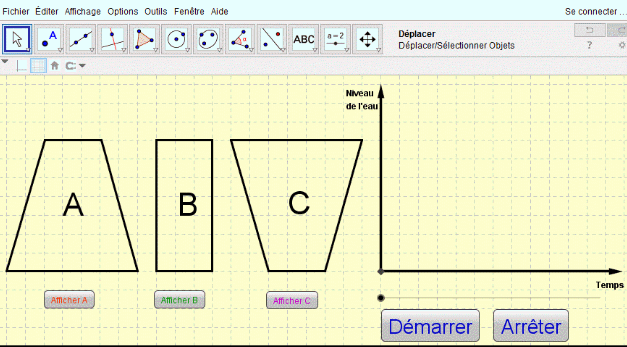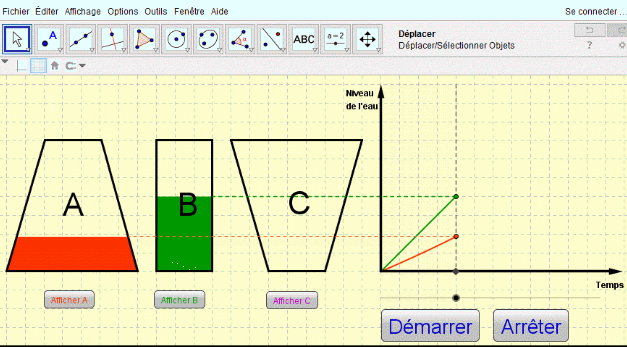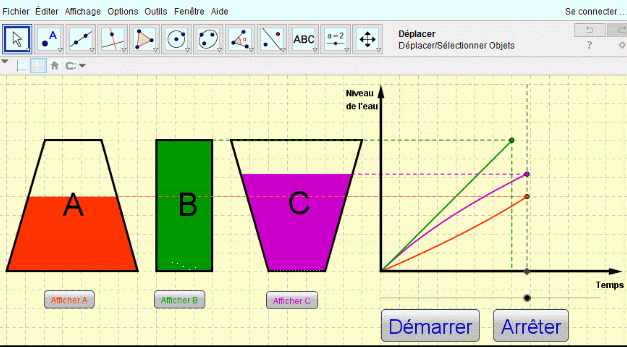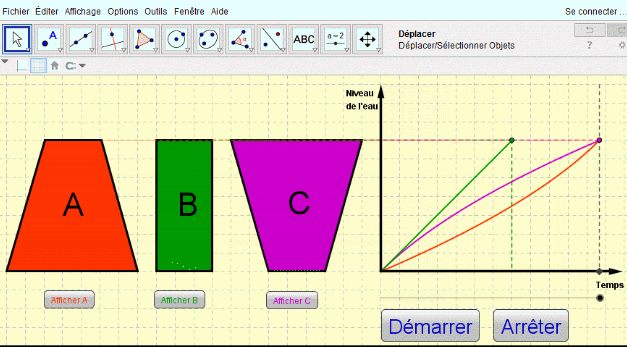
Voici un exemple de mecanisme issu des travaux GEOGEBRA de Patrick Clément
http://tube.geogebra.org/material/simple/id/72275#material/1511Cette courte animation permet de découvrir un GRAPHE qui permet d'animer un mecanisme et de modifier ses parametres de longueur et d'angle "graphiquement" sur une même figure.
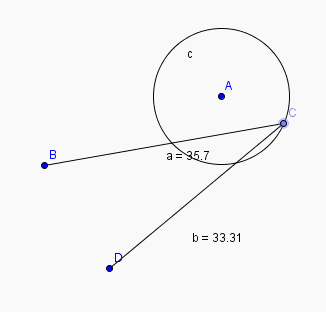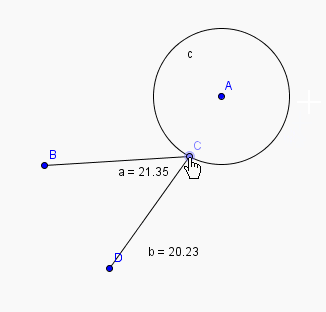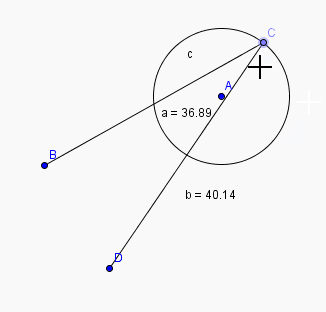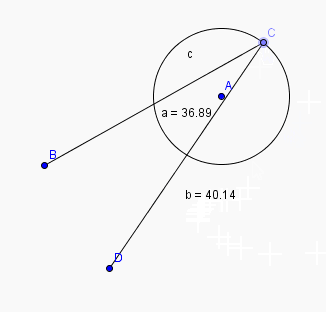
A noter qu'il est possible , entre autre , d'afficher numeriquement les parametres ( voir 2 eme anim.)la 3eme animation est plus "classique"
Chri
-
Cool Raoul! Balèze le GeoGebra!

(sinon rien à voir : ne pas rater cela! )

Aussi incroyable que cela paraît, c'est bien accessible à l'utilisateur!
Toujours gratoche pour l'étudiant, l'enthousiaste, le hobbyiste, la startUp!
-
Bon, bé fichtre!
 (tout gratoche oeuf corse)
(tout gratoche oeuf corse)
On peut refaire son Algodoo chez soi, avec ce truc de furieux!
Le p5.js (c'est du javaScript) qui se programme direct en ligne dans le navigateur!
(ça marche avec tout : de l'arduino au télescope! )
Resucée du Processing (c'est du Java) mais bon c'est quasi pareil en gros!
Question vitesse Processing, ayant vu les vidéos du sieur Daniel Shifmann - Coding Rainbow carbure en gros 3 fois plus vite que p5.js pour les bidules délicats!
Bref le p5.js a déjà plein de "libraries" dont celle-ci (p5Collide2D)avec laquelle je pense a été fait cela!
Il aurait quand même pu le dire l'Otoro!
http://otoro.net/ml/pendulum-esp-mobile/index.html Double pendule inverse!
(j'ai pas tout suivi, mais, bon, on peut interagir avec ce qui est sur l'écran!
Parce que ce qui est derrière ce truc, c'est des réflexions sur les réseaux neuronaux! Bouffre!M'enfin c'est sûr que ce p5.js c'est le truc qui va prendre de l'essor!

Une vidéo qui n'a rien à voir mais c'est du P5.js qui choppe la caméra et en bricole le résultat!

-
@pilou said:
la dose d'astuce qu'il faut avoir pour réaliser ce genre de chose!
Et de poésie! de la pure pataphysique!
-
@pilou said:
Normalement à copier cela doit être très facile, car toute la difficulté réside seulement dans la longueur respective des segments!

Il y a des trucs a connaitre du style :
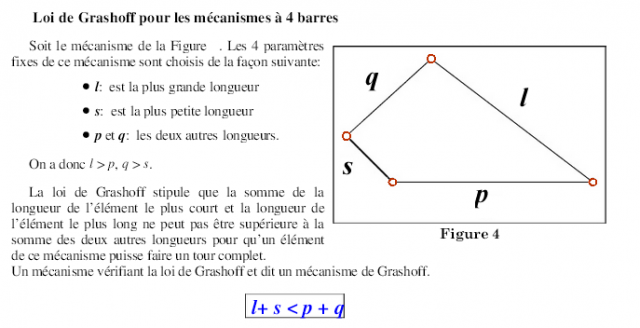
S+L ≤ P+QLa condition de Grashof d'une liaison à quatre barres est:
Si la somme de la liaison la plus courte et la plus longue d'un quadrilatère articulé planaire est inférieure ou égale à la somme des deux liaisons restantes, le lien le plus court peut pivoter complètement par rapport à une lien voisin.
En d'autres termes, la condition est satisfaite si S + L ≤ P + Q où S est la liaison la plus courte, L est la plus longue, et P et Q sont les autres lienslien
http:http://en.wikipedia.org/wiki/Four-bar_linkagechri
Advertisement