ROBOTIC LINKAGE MECHANISM simulator - ALGODOO - GEOGEBRA
-
Bon, bé fichtre!
 (tout gratoche oeuf corse)
(tout gratoche oeuf corse)
On peut refaire son Algodoo chez soi, avec ce truc de furieux!
Le p5.js (c'est du javaScript) qui se programme direct en ligne dans le navigateur!
(ça marche avec tout : de l'arduino au télescope! )
Resucée du Processing (c'est du Java) mais bon c'est quasi pareil en gros!
Question vitesse Processing, ayant vu les vidéos du sieur Daniel Shifmann - Coding Rainbow carbure en gros 3 fois plus vite que p5.js pour les bidules délicats!
Bref le p5.js a déjà plein de "libraries" dont celle-ci (p5Collide2D)avec laquelle je pense a été fait cela!
Il aurait quand même pu le dire l'Otoro!
http://otoro.net/ml/pendulum-esp-mobile/index.html Double pendule inverse!
(j'ai pas tout suivi, mais, bon, on peut interagir avec ce qui est sur l'écran!
Parce que ce qui est derrière ce truc, c'est des réflexions sur les réseaux neuronaux! Bouffre!M'enfin c'est sûr que ce p5.js c'est le truc qui va prendre de l'essor!

Une vidéo qui n'a rien à voir mais c'est du P5.js qui choppe la caméra et en bricole le résultat!

-
@pilou said:
la dose d'astuce qu'il faut avoir pour réaliser ce genre de chose!
Et de poésie! de la pure pataphysique!
-
@pilou said:
Normalement à copier cela doit être très facile, car toute la difficulté réside seulement dans la longueur respective des segments!

Il y a des trucs a connaitre du style :
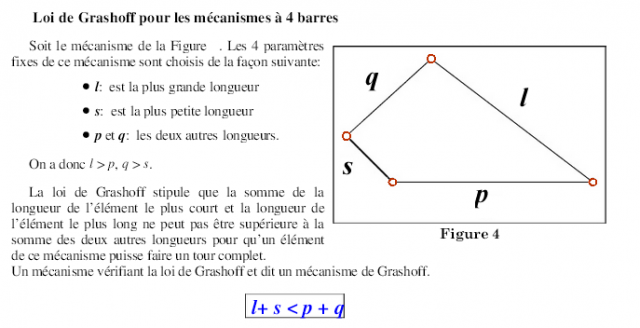
S+L ≤ P+QLa condition de Grashof d'une liaison à quatre barres est:
Si la somme de la liaison la plus courte et la plus longue d'un quadrilatère articulé planaire est inférieure ou égale à la somme des deux liaisons restantes, le lien le plus court peut pivoter complètement par rapport à une lien voisin.
En d'autres termes, la condition est satisfaite si S + L ≤ P + Q où S est la liaison la plus courte, L est la plus longue, et P et Q sont les autres lienslien
http:http://en.wikipedia.org/wiki/Four-bar_linkagechri
-
Et même devenu gratuit désormais pour les MACS!

Advertisement







