Was Pythagoras Wrong ?
-

-
Flat them from the diagonal's middle to the diagonal, seems they will exceed

Visible as the first division
-
If you keep subdividing, eventually there will be an infinite number of sub-divisions. But in order to traverse the line, the subdivisions cannot be of zero length otherwise there would only be a point. Infinite divisions * non-zero length = the hypoteneuse is infinite!

And as Douglas Adams pointed out in the Hitch Hiker's Guide... if there are a finite number of sentient beings occupying an infinite universe, then any answer is pointless as it is infinitely probable that your post was just a figment of my imagination!
-
Welcome in Manhattan...
https://en.wikipedia.org/wiki/Taxicab_geometry (Manhattan Metric) -
Of course I realize all of this...

BUT don't you think it's incredibly "counter-intuitive" that 2*zillion steps each of a zillion-th in length ALWAYS ends up with 2... and never gets to be be the obvious length sqrt(2) [you can even 'measure' it to an approximation] !
AND calculus's differentiation/integration relies on 'tending to zero' to get the right answer - here as you 'tend to zero' the length remains 2 !
We know the length of the hypotenuse is sqrt(2)... but then
-
This is also very useful for route length estimation.
If you are in a city and want to find the shortest way from A to B, but you don't have Google Maps:
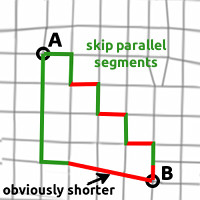
Of all suggested routes you can skip parallel segments (that follow a Manhattan street raster). If streets are not exactly parallel, you just estimate the difference. -
Tig, your argument has two errors: one, you start with one unit of measurement (meters), and then switch to an ambiguous "unit"; second, the equation you use in the second and subsequent examples (1/2 x 4 = 2) is not the pythagorean theorem.
If using the theorem, and units, consistently, it holds true:
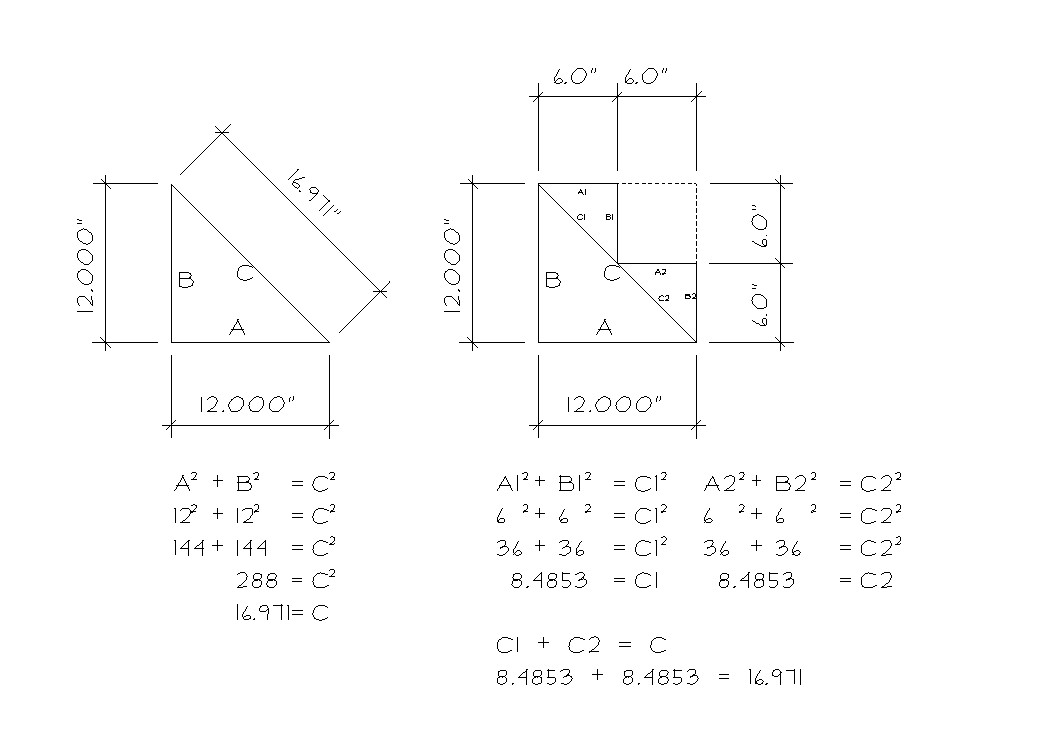
-
This is all geek to me.
-
Daniel, you misunderstand.
I did not propose to show any 'Pythagorean calculations' at all.
In fact I think you'll find that Pythagoras never did any calculations either - rather for him it was all about proportions, ratios and the like - and indeed he was very uncomfortable with proportions that ended in things like sqrt(2) which is irrational and can never be reduced to a whole number, no matter how much you adjust the ratios of the other sides - which of course went against his entire belief system that everything good be reduced to whole number ratios, even if they turned out to be very large - you just need to keep working at it...In your example you simply keep working out the hypotenuses, which will never change so that answer will always be the same too - just as when I work out the 'steps' it's always '2' too...
What I was trying to show is that what we 'know' to be true from opp^2+adj^2=hyp^2 i.e. hyp=sqrt(opp2+adj2), and from the more prosaic fact that we can 'measure' the length of the hypotenuse of a right-angled triangle with sides of '1' and find that it's ~1.414.. [
 Incidentally I said 1m for the sides to get a 'perspective' of what was done. I never and jumped into other 'units' ?? did I ? When I say '2 units' 2m is implied as this was the 'units' we started with! In all geometry the actual 'dimensions' are irrelevant - it's the relationships [ratios] of the sides etc that matters, as a triangle with sides of 2 cubits has a hypotenuse of 2*sqrt(2) cubits ! - and if you omit the 'cubits' and add 'miles' it still works...] ... what we 'know' goes again some "intuitive response" to the fact that as we 'step' the sides in, dividing in half every time to make smaller and smaller 'zig-zags' and then multiplying by the increasing number of these steps it always remains '2' - even when the steps become so tiny that the zig-zag 'line' approximates to the hypotenuse itself. The hypotenuse is clearly 'sqrt(2)' long... but the stepped line that effectively overlays it is always '2' units long, no matter how tiny its steps become - so the minisculely stepped edge-set is about ~40% longer than the 'straight line' hypotenuse that it approximates to... So another way to think about it is... OK, the stepped version is 'crinkled up' by these zig-zags, but when these are so tiny the two overlay each other 'exactly' - at least for all intents and purposes - so... where has ~40% of the stepped line 'gone' ?
Incidentally I said 1m for the sides to get a 'perspective' of what was done. I never and jumped into other 'units' ?? did I ? When I say '2 units' 2m is implied as this was the 'units' we started with! In all geometry the actual 'dimensions' are irrelevant - it's the relationships [ratios] of the sides etc that matters, as a triangle with sides of 2 cubits has a hypotenuse of 2*sqrt(2) cubits ! - and if you omit the 'cubits' and add 'miles' it still works...] ... what we 'know' goes again some "intuitive response" to the fact that as we 'step' the sides in, dividing in half every time to make smaller and smaller 'zig-zags' and then multiplying by the increasing number of these steps it always remains '2' - even when the steps become so tiny that the zig-zag 'line' approximates to the hypotenuse itself. The hypotenuse is clearly 'sqrt(2)' long... but the stepped line that effectively overlays it is always '2' units long, no matter how tiny its steps become - so the minisculely stepped edge-set is about ~40% longer than the 'straight line' hypotenuse that it approximates to... So another way to think about it is... OK, the stepped version is 'crinkled up' by these zig-zags, but when these are so tiny the two overlay each other 'exactly' - at least for all intents and purposes - so... where has ~40% of the stepped line 'gone' ? 
-
So let's get rid of square houses!
4×3 or 5×12 or 8×15 or 13×84 houses are much nicer!
(And you don't need a calculator) -
@aerilius said:
So let's get rid of square houses!
4×3 or 5×12 or 8×15 or 13×84 houses are much nicer!
(And you don't need a calculator)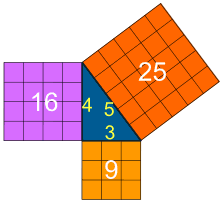
Pythagoras loved 3/4/5 triangles and their ilk. They were three sides in perfect ratios of whole numbers... and other triangles that were 'similar', but with 'fractional' edge lengths, could be reduced/increased pro rata to these 'pure' whole numbers.
He believed that the whole universe worked on ratios of whole numbers, the fact that the hypotenuse of a 1x1 triangle was 1.414.. to him meant that if it were 1000x1000 the hypotenuse would be 1414, if it wasn't quite whole 'yet' then simply ramping up would do it... so sides of 1000000 each give a hypotenuse of 1414213 - unfortunately because some square roots like this are 'irrational' [as are some other important numbers like Pi/Tau] - no matter how big you made the three sides you'll never get to a point where all of them have whole number lengths. Pythagoras didn't like this concept at all and thought it a limitation of his/our abilities [he'd have used geometry/drawing to apportion squares to sides, ever smaller until the approximation was good enough but never 'there'] - he thought that eventually someone would work out how to 'fix it'... but no one ever will

[xxl-img:3qpbio08]http://www.takayaiwamoto.com/Pythagorean_Theorem/Euclid_47_7_anim.gif[/xxl-img:3qpbio08]
-
Was Pythagoras wrong?
yes.
-
@unknownuser said:
He believed that the whole universe worked on ratios of whole numbers
Numbers, or maths or geometry exist only because we are existing! - 7 000 000 years very first ones

Does they are existing at the dinosaurs' times ?
 - 65 000 000 years last one
- 65 000 000 years last one -
So the sum of two sides of any isosceles right triangle = 2?
Solution must be done for a more general case of any right triangle and if it still equals two I'll be a believer -
@tig said:
OK, the stepped version is 'crinkled up' by these zig-zags, but when these are so tiny the two overlay each other 'exactly' - at least for all intents and purpose
Ah, but surely that is not quite right. A true line has not just infinitesimal thickness, but exactly zero thickness (think of the boundary between the inside and outside of a solid; how "thick" is it.) So the steps cannot overlay the edge, because a true line has no "area" to overlay. The hypoteneuse length is a distance between two points, not a measure of the amount of graphite we lose from our pencil as we draw an imperfect representation of the vector.
We could even say that the stepped "approximation" is really a fractal, lying somewhere between a being line (one dimension) and filling an area (two dimensions). -
The fractal analogy is a good one.
Although with fractals the more carefully you measure along a fractal perimeter the longer it gets - like measuring a coastline from headland to headland gives a shorter coastline length than measuring it rock to rock, or even more accurately pebble to pebble, or grain-of-sand to grain-to-sand etc...
Here the length of steps is constant no matter how much we subdivide it
Clearly any straight line between two points is going to be shorter that a set of zig-zag steps between those two points...
I just find it weird that the stepped versions is ~40% longer, even when the steps are so tiny it for all practical purposes overlays the straight line.
I know a 'geometric' straight line has no thickness and a stepped set will be event when this stepped set's 'thickness' tends to zero it doesn't change its total length.
Think of it another way...
You are going to lay carpet onto a flight of steps [treads and risers] - including a top tread so there are equal numbers of treads and risers, that's just in case anyone is thinking of getting clever .
.
Let's assume the steps are at 45 degrees - I know that these are too steep for any Regulations, but hey this is theoretical !
You could measure every tread and every riser individually and add up the lengths.
If you has confidence that the steps were the same you could alternatively measure one pair and multiply the answer by the number of them.
OR a quick way that avoids even counting the pairs is to measure the total going of the steps in plan [+ a tread!] and the total rise [up]. Add the two together and the answer is as if you totted up all of the parts...
So now we have the length of carpet needed to do this, notice how it is independent of the number of steps - it relies solely on the going/rise dimensions.
Now let us assume we decide to replace the steps with a ramp sloping from the bottom of every riser to the topmost landing-tread's back-edge [i.e. the edge away from the topmost 'nosing'].
OK, it's steep but let's not get bogged down in 'Regulations'...
The length of carpet need for the surface ramp is ~40% less than if you carpeted the treads/risers !
But now let's do a 'thought-experiment'...
You take the stepped version with its carpeting and increase the number of steps in increments of say twos. We already know that the number of steps is actually irrelevant as the total length of carpet remains constant no matter how many or how few steps there are. But when you get to a zillion-zillion steps, then for all intents and purposes the stepped flight 'looks' the same as the 'ramped' version. However, the stepped flight will use 40% more carpet, although it appears to be just the same to the observer.
With an electron-microscope we'd see the myriad folds of carpet as it rippled down the stepped version but from a day-to-day practical view-point they are the 'same surface'.
I find it fascinating that really tiny geometry can 'fold in on itself' in this manner, after all that ~40% costs money and is unneeded !!
Calculus [put overly simplistically] relies on making tinier and tinier slices until 'in the limit it tends to zero', then we add up the bits to get the answer... This is almost the exact the opposite - making tinier and tinier steps gets us no nearer the straight-line's length, the stepped size is fixed irrespective of the number of steps. -
Isn't all this similar to an island's area being finite whereas its shoreline is --- practically --- infinite?
-
@chrisglasier said:
Isn't all this similar to an island's area being finite whereas its shoreline is --- practically --- infinite?
Correct.
You can do a similar 'proof' that Pi is 4 !
You draw a square with a circle inside so the diameter=side length.
You start adding smaller squares into the parts of the original touching the circumference.
Each division is redivided ad nauseam until we have a zig-zag star-like 'polygon' that approximates to the circle's circumference.
Since we know that the circle's circumference is PiD the perimeter of the 'polygon' should be approaching this as we made it progressively nearer and nearer a circle - after all the area of the circle and the 'shrinking' polygon will surely be 'converging' ?
But the cruncher is just like the 'steps' - the perimeter of the 'polygon' is always 4D - so Pi=~4 doh!
Although the areas get nearer and nearer they never match and the perimeters never converge at all ! -
That's if you define π by the circle's circumfence (2×r×π), but what if you define it by its area (r²×π) and sum up infinitely small squares?
How can we know that a dimension that we try to measure could not be defined in any alternative way, leading to a completely different result?
-
@tig said:
practical purposes
I would suggest that here is the nub of the problem.
Geometry is a only theoretical model for the shapes we find in the world around us. Just as Newtonian physics breaks down at velocities beyond our ability to comprehend, so using pure geometry on practical materials has an inherent "bandwidth" beyond which its axioms cannot be applied.
The steps never converge on the straight line because they do not have to exist at an arbitrary, humanly intuitive scale - nor be constructed of the physical units of the real universe (atoms, molecules etc.) Hence my fractal analogy - as purely abstract entities, the steps retain their geometric properties no matter how small we make them, because there is no absolute measure of "smallness" in pure unit-less geometry, only the relative scale of the parts of a form.
In reality, the carpet analogy breaks down at some point where the thickness of carpet, and minimum bend radius, grossly exceed the size of the steps. So it is a category error - we are applying an abstract mathematical theory in a situation where its axioms are not valid.
That is a valuable lesson that is all too rarely taught in school science etc. For example, the inverse square rule applied to the intensity of light, sound, gravity etc, is often used blindly - but the light intensity from a strip light within a room does not follow this, because the assumption of a point-source is broken.
Advertisement







