CURIOSITE GEOMETRIQUES
-
Idem pour un convave!


PS Au fait, ce ne sont pas plutôt des curiosités géométriques ?
-
@pilou said:
Idem pour un convave!

PS Au fait, ce ne sont pas plutôt des curiosités géométriques ?
Tu as raison , j'ai modifié le titre du POST
AmicalementChri
-
Ce qui d'ailleurs montre un bug du forum!

Si l'on change le titre général, le titre de chaque post lui, n'est pas changé!
-
@pilou said:
Ce qui d'ailleurs montre un bug du forum!

Si l'on change le titre général, le titre de chaque post lui, n'est pas changé!
C'est normal puisque, même si on ne le fait jamais, on peut titrer chaque intervention comme on veut. Par défaut c'est "Re: Titre actuel de la conversation" mais on peut mettre n'importe quoi de plus explicite.

-
...puisque c'est ma marque de fabrique sur le forum ZBrush!

J'en profite, mais conceptuellement c'est pas naturel!

La priorité devrait être donnée au créateur du fil!
-
Bonj
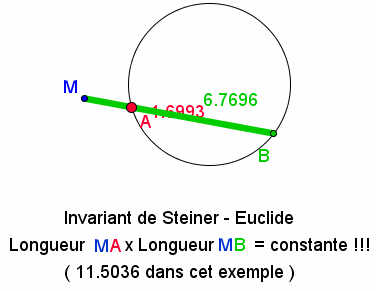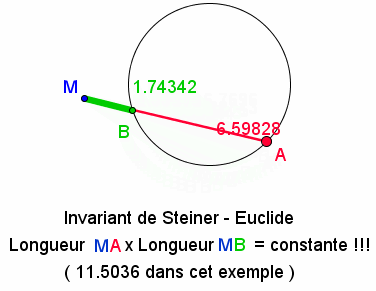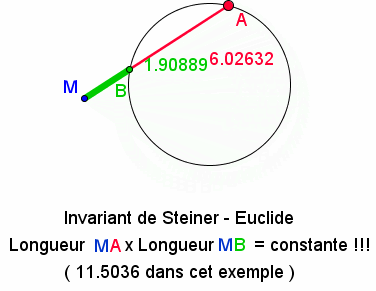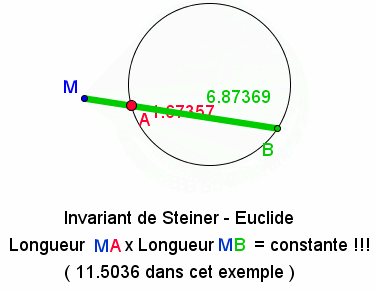
une autre curiosité bien cachée derrière notre quotidien ,l'invariant de Steiner .
Soit un point M, une droite qui coupe un cercle en A et B , Le produit MAxMB reste constant
!!!vous pouvez faire des copies d'écran et faire le calcul si vous doutez.
bon !
source : http://www.maths-et-tiques.fr/index.php/detentes-55
-
@chri said:
une autre curiosité bien cachée derrière notre quotidien ,l'invariant de Steiner .
Soit un point M, une droite qui coupe un cercle en A et B , Le produit MAxMB reste constant
!!!Aïe ! celle-là, elle m'avait fait mal il y a 30 ans quand j'ai tenté de comprendre une des solutions au problème de Napoléon (trouver le centre d'un cercle à l'aide d'un compas seulement). C'est pas intuitif cette constante, et pourtant c'était déjà énoncé par Euclide !
-
Ah les proportions, les produits, les leviers... donnez-moi un assez grand levier et je vous soulèverais le monde!

Pour le reste...
j'ai pas trop l'humeur car un enfoiré m'a dérobé mon ordi portable!
-
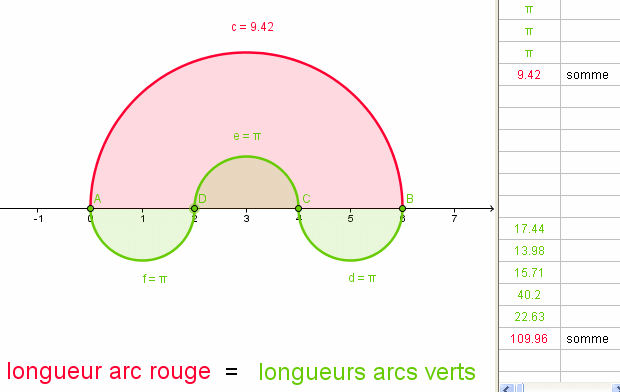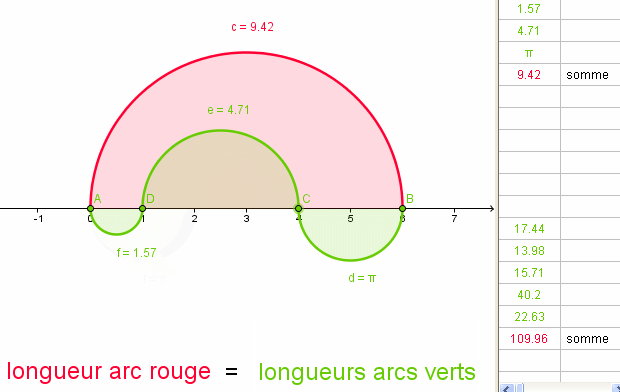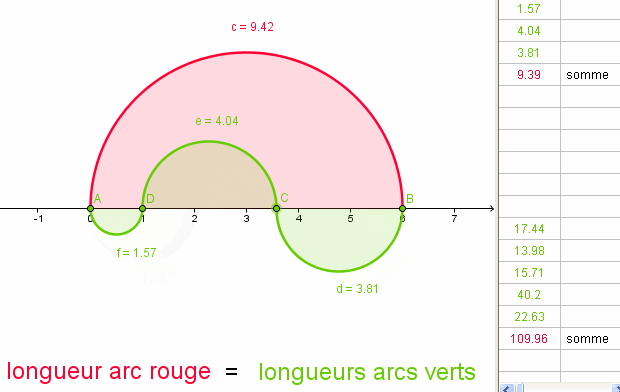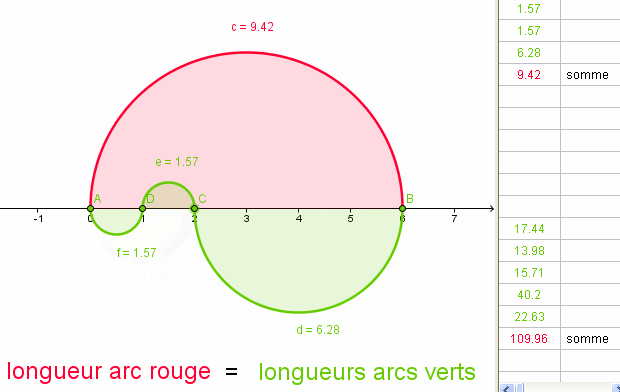
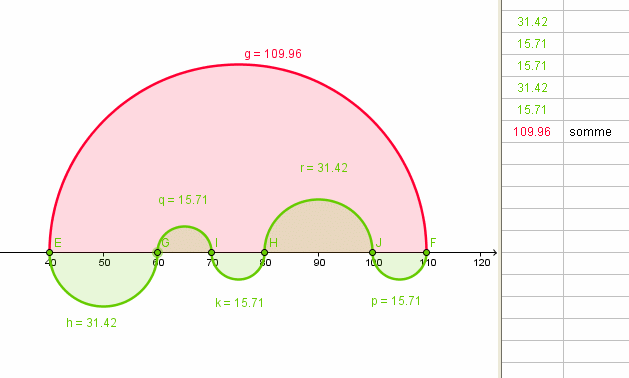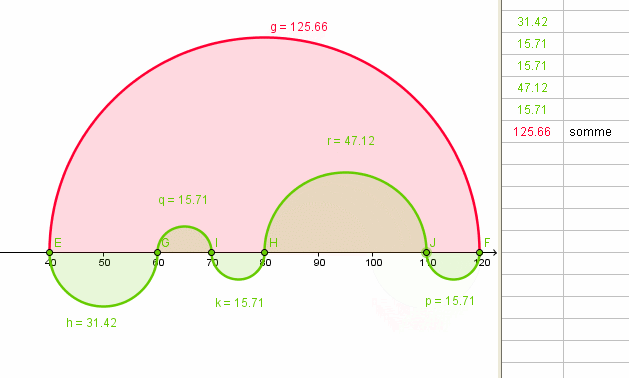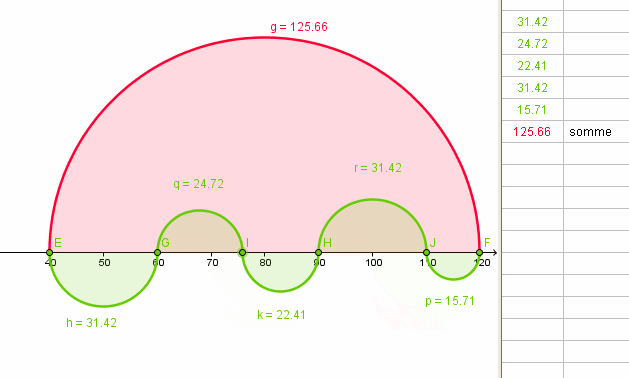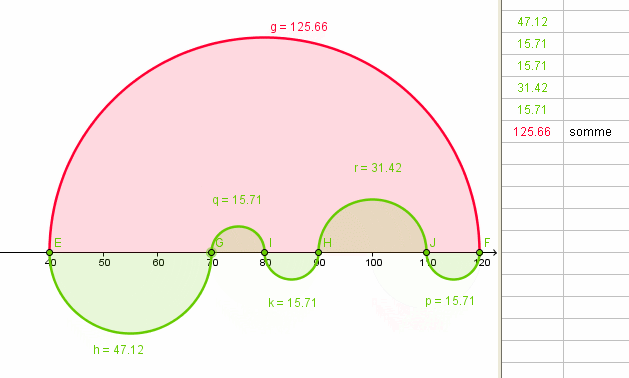
Et HOP , une autre !
logiciels GEOGEBRA - GifCam
remarque :
Les longueurs des arcs rouges et verts restent égales si l'on déplace les nœuds sur l'axe des X .a+
Chri
-
Bonjour
Trouvez ci-joint un exemple des vidéo de Mickaël Launay
le theme de celle-ci : Les hexaflexagones
https://www.youtube.com/watch?v=aQo8tYQuWQw[highlight=#ffff80:15w94p0x]Bien écouter son commentaire de la minute 3.38[/highlight:15w94p0x]

a+
Chri

-
Les Kaléidocyles! Ouf, je vais pouvoir me coucher tranquille!

ben non !Celle-ci n'est pas mal non plus , quoique plus basique
https://www.youtube.com/watch?v=5xlVUG8qrWMchri
a+

-
Rigolo ça, dans le temps ils vendaient un truc un peu similaires avec des dessins d'Eicher, on obtenait un genre de ruban de Moebius(?) constitué de triangles(?) que l'on pouvait tourner sur eux-mêmes vers l'intérieur à l'infini tout en changeant le "dessin"!

Encore plus plaisant à manipuler que son bidule hexaflexatoire!
Maintenant le hic, c'est comment s'appelait ce bidule!
Le gars a dû en parler dans ses autres vidéos qui sait!
Bon pas de bol, il en parle pas et ce n'est pas non plus sur son étagère!

IL va falloir que je retrouve cela sur le Net!
Voilà c'était ce genre là!

Les Kaléidocyles! Ouf, je vais pouvoir me coucher tranquille!
-
Le problème de tous ces trucs que l'on manipule, c'est qu'ils sont hyper fragiles car en carton ou papier et qu'ils se déchirent très vite!

Mais sinon sûr que c'est un domaine de recherche formelle fascinant!
D'ailleurs le Net en pullule
Malin le truc du cube!
Ce qui serait cool c'est de faire la même chose sur les 3 axes!
Un cube de cubes quoi
-
Pas que!

-
@pilou said:
Mais sinon sûr que c'est un domaine de recherche formelle fascinant!
D'ailleurs le Net en pullule
Je suis d'accord avec toi, quand on commence ... c'a n'a plus de fin.
On surfe comme des chiens fous ( si tenté que les chiens surfent )Je viens de vérifier , les chiens surfent aussi

bonne nuita+
-
@chri said:
Bonjour
Trouvez ci-joint un exemple des vidéo de Mickaël Launay
le theme de celle-ci : Les hexaflexagonesGénial ! J'ai rencontré les hexaflexagones dans Jeux et Stratégie en 1981, dans le numéro 8 (oui, j'ai ressorti ma collec pour trouver ça
 ). Merci pour cette piqure de rappel... je vais fouiller dans les J&S pour voir s'il n'y a pas de bonnes idées pour mes étudiants
). Merci pour cette piqure de rappel... je vais fouiller dans les J&S pour voir s'il n'y a pas de bonnes idées pour mes étudiants 
-
Bonj
Pour les Parisiens ...
le 16eme salon culture et mathématiques aura lieu du jeudi 28 au dimanche 31 mai 2015 sur la place Saint Sulpice dans le 6e arrondissement de Paris.
lien :
http://www.cijm.org/salona+
Chri

-
Si je suis dans lecoin, j'irais voir, surtout qu'il y a le découvreur des trous noirs (JP Luminet) enfin théoriques parce que moi, je suis comme Saint Thomas, si je ne le vois pas, je ne le crois pas!

Programme un peu plus musclé que le concours Lépine!
-
@pilou said:
Si je suis dans lecoin, j'irais voir, surtout qu'il y a le découvreur des trous noirs (JP Luminet) enfin théoriques parce que moi, je suis comme Saint Thomas, si je ne le vois pas, je ne le crois pas!

Programme un peu plus musclé que le concours Lépine!
Je te propose qu'on en reparle.
Chri -
Pilou les liens sont identiques..
(il y en a un qui suit, dans la salle )
)
Advertisement







