CURIOSITE GEOMETRIQUES
-
Bonjour
Trouvez ci-joint un petit exemple surprenant :
Je vous propose de :
1 - Tracer 1 quadrilatère de sommets A B C D quelconques sur 1 plan
2 - tracer le segment qui joint le milieu de AB au milieu de BC
3 - tracer le segment qui joint le milieu de BC au milieu de CD
4 - tracer le segment qui joint le milieu de CD au milieu de DA
4 - tracer le segment qui joint le milieu de DA au milieu de ABQue pensez-vous des cotés , 2 a 2 , de ce nouveau quadrilatère ?
Chri
source GEOGEBRA
-
Click droit / Info sur l'entité!

-
@chri said:
RESULTAT DU JEU
en traçant un quadrilatère quelconque , le quadrilatère dessiné sur les points milieu a des arêtes parallèles 2 a 2.
chri
Génial !! C'est une application directe du théorème de Thales, c'est logique : chaque segment dessiné est parallèle à la diagonale du quadrilatère et de la moitié de la longueur de celui-ci. Sans le dessiner je ne l'avais pas deviné !!
Merci, je garde ça sous le coude pour un cours de géométrie, pour surprendre mes étudiants à mon tour
Merci Chri ! -
C'est pas seulement quelles sont parallèles (trivial), c'est qu'elles sont d'égales longueurs deux à deux!

Encore plus boulversifiant!
-
@pilou said:
C'est pas seulement quelles sont parallèles (trivial), c'est qu'elles sont d'égales longueurs deux à deux!

Encore plus boulversifiant!
Heu... si les coté sont parallèles deux à deux, on a un parallélogramme, donc d'égales longueur.
Ou l'inverse, si on a un quadrilatère dont les longueurs des cotés opposés sont égales, c'est un parallélogramme donc les cotés sont parallèles.
De toute façon, dans les deux démonstrations on passe par Thalès, ça limite le champ d'exploration à ce qu'on collégien devrait connaitre. Peu importe dans quel sens va la démonstration, on arrive au parallélogramme qui regroupe les deux points de vue
-
[highlight=#ffff00:39gt86p0]RESULTAT DU JEU[/highlight:39gt86p0]
en traçant un quadrilatère quelconque , le quadrilatère dessiné sur les points milieu a des arêtes parallèles 2 a 2.
chri
-
Et une illustration , une , pour en finir
Chri
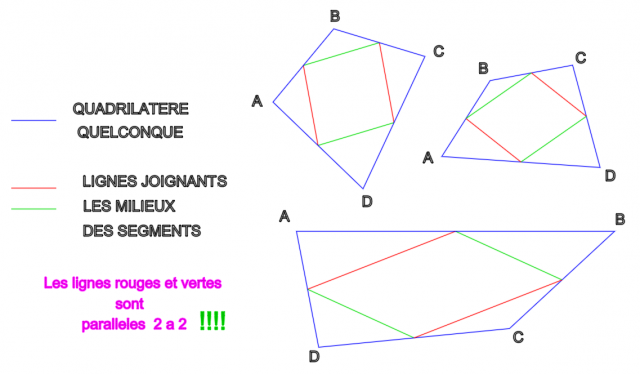
-
Et égales 2 à 2 !

-
et égales 2 a 2
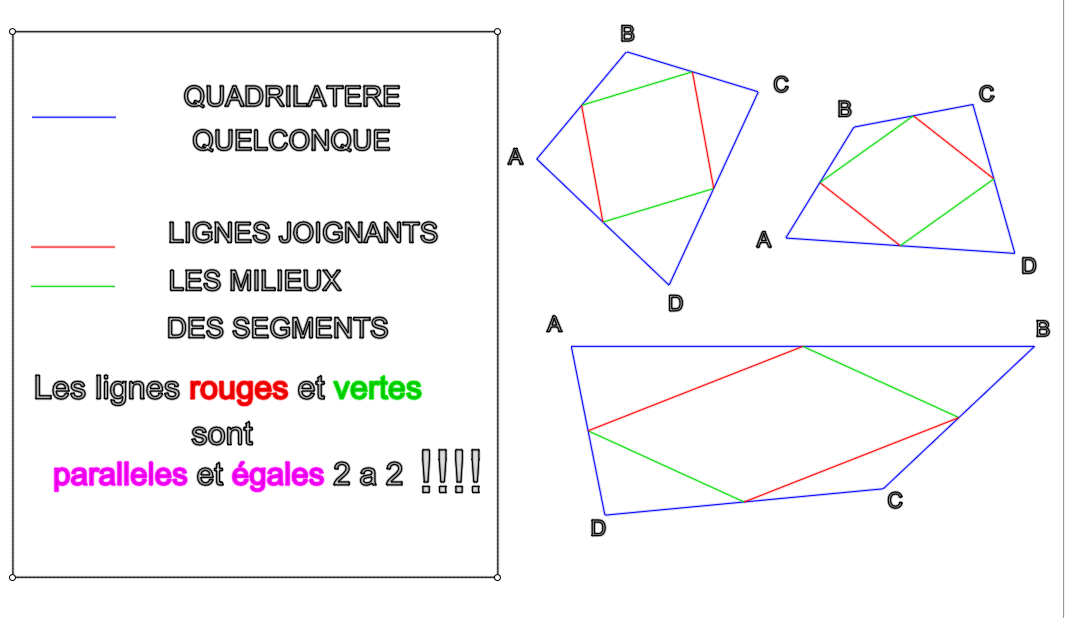
-
... parallèles aux diagonales du quadrilatère de départ et la longueur de chaque coté est la moitié de la longueur de la diagonale associée (les vertes = 1/2 AC et les rouges 1/2 BD)

-
@daredevil said:
... parallèles aux diagonales du quadrilatère de départ et la longueur de chaque coté est la moitié de la longueur de la diagonale associée (les vertes = 1/2 AC et les rouges 1/2 BD)

Bon , j'ai compris , nouveau dessin !
BRAVO mon pote
Chri
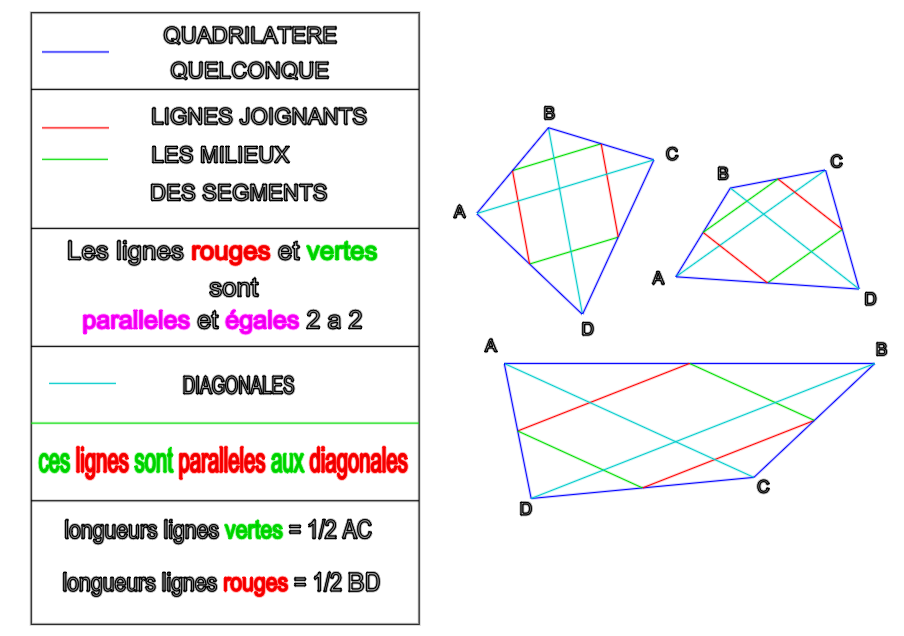
-
Et si on parlai des surfaces
Chri
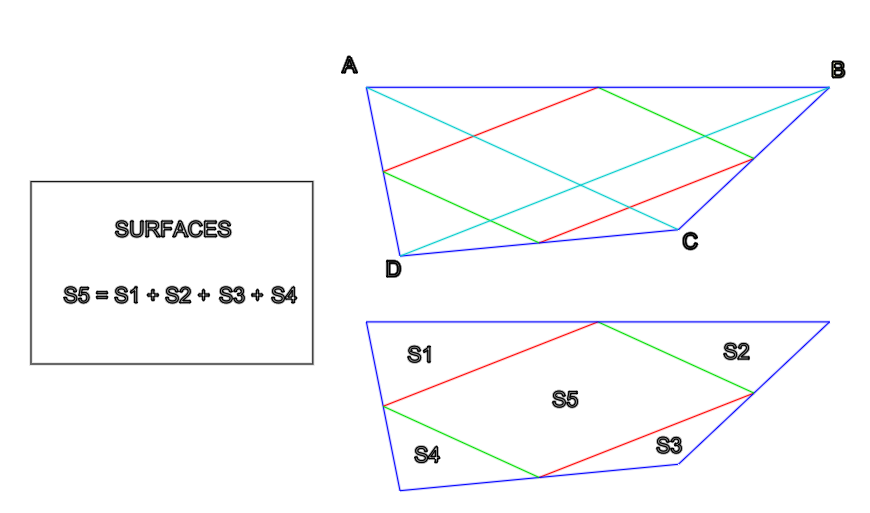
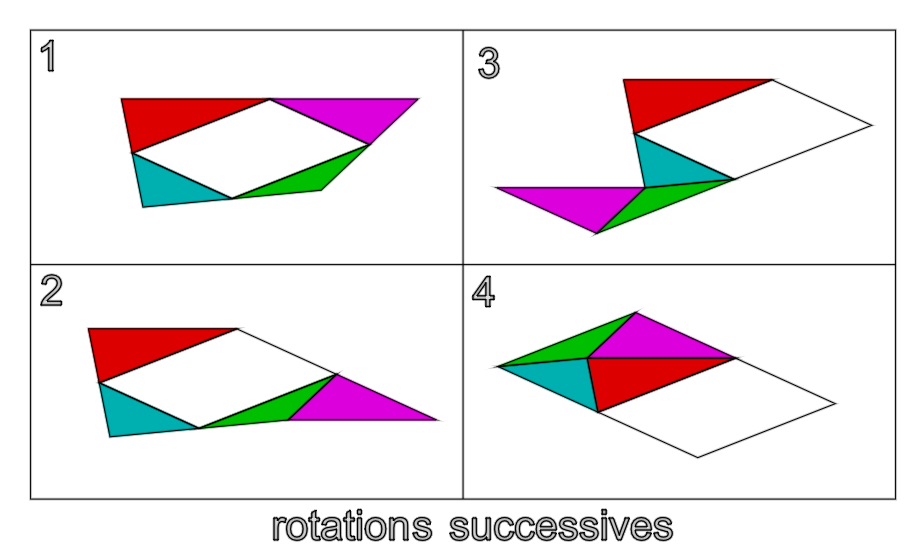
-
Marche aussi si le quadrilatère est "concave"!

Le non parallélisme n'est dû qu'à l'effet de perspective!
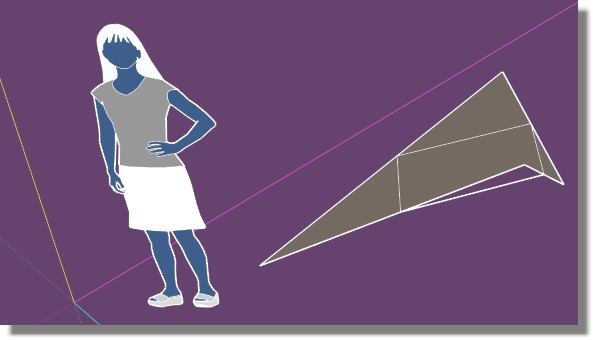
-
Il y a de quoi faire une thèse sur le sujet !!

-
@daredevil said:
Il y a de quoi faire une thèse sur le sujet !!

Un certain THALES , Jean-Luc ou Maurice , je ne me souvient plus l'a déjà faite !
Chri
-
Thales, Thales, c'est pas un gars qui fait des fusées ça ?

Oui, oui, j'y vais !! ----> []
-
@chon said:
Thales, Thales, c'est pas un gars qui fait des fusées ça ?

Oui, oui, j'y vais !! ----> []
lol
-
Bonjour à tous
Ce que nous venons de découvrir aujourd'hui a été découvert par MR VARIGNON qui vécu de 1654 à 1722 .
Si vous tapotez : Théorème de VARIGNON ... alors aie , aie , aie ... nouveau voyage internet !
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Varignon
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Quadrila.htm
http://www.le-triangle-et-ses-calculs.ch/index_varignon.phphttps://tube.geogebra.org/search/perform/search/varignon
....Salutations
Chri
-
Bonjour
Suite à cet exemple , trouvez ci-après d'autres théorèmes de géométrie assez sympa.
avec images jointes
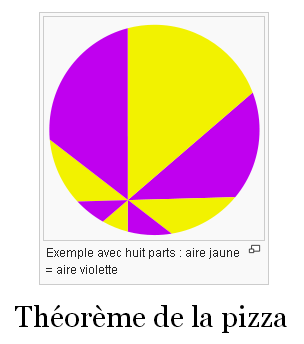
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_la_pizza
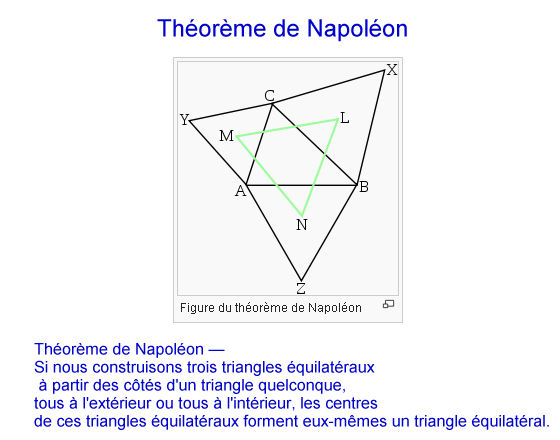
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Napol%C3%A9on
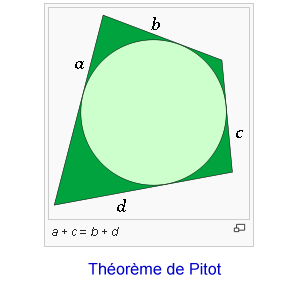
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Pitot
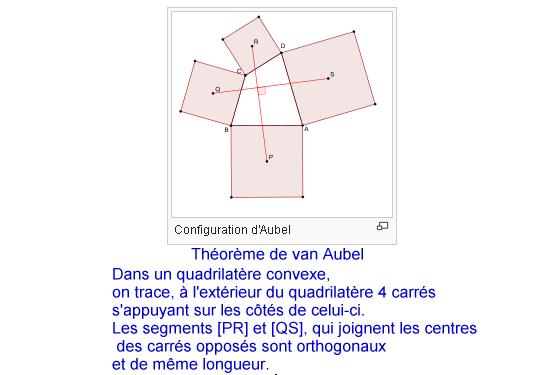
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_van_Aubel
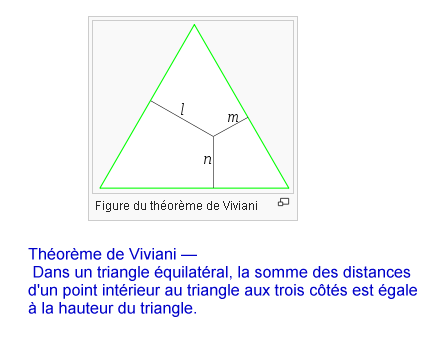
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_VivianiUn grand classique
CERCLE D'EULER ou des neuf points
http://villemin.gerard.free.fr/GeomLAV/Cercle/Neufpoin.htmd'autres plus complexes :
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Brahmagupta
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Miquel
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Morley
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Ptol%C3%A9m%C3%A9e
http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Wallace-Bolyai-GerwienSalutations
Chri

-
RE
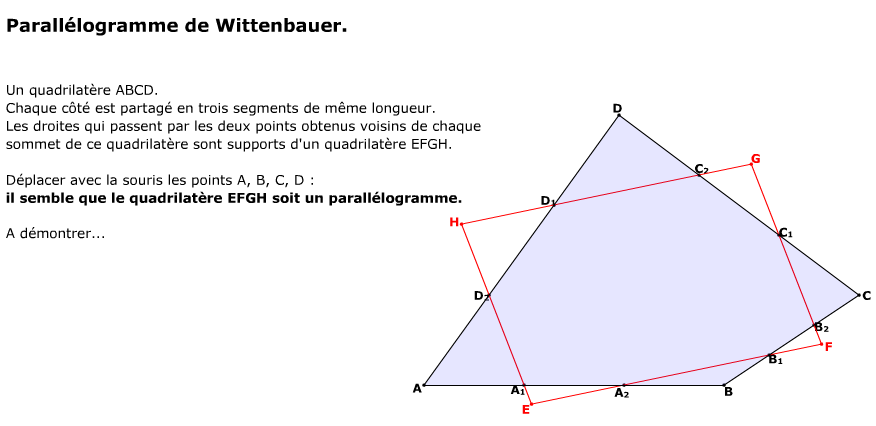
En voici un autre du même acabit :
Ce qui me fait songer que pour le 1er , les segments étaient coupés en 2 , dans celui ci , en 3 ..... qu'est-ce qui ce passe pour nb>3 ?
http://rdassonval.free.fr/flash/flash2014.html
http://rdassonval.free.fr/flash/wittenbauer.swfChri
Advertisement







