Was Pythagoras Wrong ?
-
@aerilius said:
So let's get rid of square houses!
4×3 or 5×12 or 8×15 or 13×84 houses are much nicer!
(And you don't need a calculator)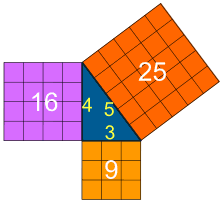
Pythagoras loved 3/4/5 triangles and their ilk. They were three sides in perfect ratios of whole numbers... and other triangles that were 'similar', but with 'fractional' edge lengths, could be reduced/increased pro rata to these 'pure' whole numbers.
He believed that the whole universe worked on ratios of whole numbers, the fact that the hypotenuse of a 1x1 triangle was 1.414.. to him meant that if it were 1000x1000 the hypotenuse would be 1414, if it wasn't quite whole 'yet' then simply ramping up would do it... so sides of 1000000 each give a hypotenuse of 1414213 - unfortunately because some square roots like this are 'irrational' [as are some other important numbers like Pi/Tau] - no matter how big you made the three sides you'll never get to a point where all of them have whole number lengths. Pythagoras didn't like this concept at all and thought it a limitation of his/our abilities [he'd have used geometry/drawing to apportion squares to sides, ever smaller until the approximation was good enough but never 'there'] - he thought that eventually someone would work out how to 'fix it'... but no one ever will

[xxl-img:3qpbio08]http://www.takayaiwamoto.com/Pythagorean_Theorem/Euclid_47_7_anim.gif[/xxl-img:3qpbio08]
-
Was Pythagoras wrong?
yes.
-
@unknownuser said:
He believed that the whole universe worked on ratios of whole numbers
Numbers, or maths or geometry exist only because we are existing! - 7 000 000 years very first ones

Does they are existing at the dinosaurs' times ?
 - 65 000 000 years last one
- 65 000 000 years last one -
So the sum of two sides of any isosceles right triangle = 2?
Solution must be done for a more general case of any right triangle and if it still equals two I'll be a believer -
@tig said:
OK, the stepped version is 'crinkled up' by these zig-zags, but when these are so tiny the two overlay each other 'exactly' - at least for all intents and purpose
Ah, but surely that is not quite right. A true line has not just infinitesimal thickness, but exactly zero thickness (think of the boundary between the inside and outside of a solid; how "thick" is it.) So the steps cannot overlay the edge, because a true line has no "area" to overlay. The hypoteneuse length is a distance between two points, not a measure of the amount of graphite we lose from our pencil as we draw an imperfect representation of the vector.
We could even say that the stepped "approximation" is really a fractal, lying somewhere between a being line (one dimension) and filling an area (two dimensions). -
The fractal analogy is a good one.
Although with fractals the more carefully you measure along a fractal perimeter the longer it gets - like measuring a coastline from headland to headland gives a shorter coastline length than measuring it rock to rock, or even more accurately pebble to pebble, or grain-of-sand to grain-to-sand etc...
Here the length of steps is constant no matter how much we subdivide it
Clearly any straight line between two points is going to be shorter that a set of zig-zag steps between those two points...
I just find it weird that the stepped versions is ~40% longer, even when the steps are so tiny it for all practical purposes overlays the straight line.
I know a 'geometric' straight line has no thickness and a stepped set will be event when this stepped set's 'thickness' tends to zero it doesn't change its total length.
Think of it another way...
You are going to lay carpet onto a flight of steps [treads and risers] - including a top tread so there are equal numbers of treads and risers, that's just in case anyone is thinking of getting clever .
.
Let's assume the steps are at 45 degrees - I know that these are too steep for any Regulations, but hey this is theoretical !
You could measure every tread and every riser individually and add up the lengths.
If you has confidence that the steps were the same you could alternatively measure one pair and multiply the answer by the number of them.
OR a quick way that avoids even counting the pairs is to measure the total going of the steps in plan [+ a tread!] and the total rise [up]. Add the two together and the answer is as if you totted up all of the parts...
So now we have the length of carpet needed to do this, notice how it is independent of the number of steps - it relies solely on the going/rise dimensions.
Now let us assume we decide to replace the steps with a ramp sloping from the bottom of every riser to the topmost landing-tread's back-edge [i.e. the edge away from the topmost 'nosing'].
OK, it's steep but let's not get bogged down in 'Regulations'...
The length of carpet need for the surface ramp is ~40% less than if you carpeted the treads/risers !
But now let's do a 'thought-experiment'...
You take the stepped version with its carpeting and increase the number of steps in increments of say twos. We already know that the number of steps is actually irrelevant as the total length of carpet remains constant no matter how many or how few steps there are. But when you get to a zillion-zillion steps, then for all intents and purposes the stepped flight 'looks' the same as the 'ramped' version. However, the stepped flight will use 40% more carpet, although it appears to be just the same to the observer.
With an electron-microscope we'd see the myriad folds of carpet as it rippled down the stepped version but from a day-to-day practical view-point they are the 'same surface'.
I find it fascinating that really tiny geometry can 'fold in on itself' in this manner, after all that ~40% costs money and is unneeded !!
Calculus [put overly simplistically] relies on making tinier and tinier slices until 'in the limit it tends to zero', then we add up the bits to get the answer... This is almost the exact the opposite - making tinier and tinier steps gets us no nearer the straight-line's length, the stepped size is fixed irrespective of the number of steps. -
Isn't all this similar to an island's area being finite whereas its shoreline is --- practically --- infinite?
-
@chrisglasier said:
Isn't all this similar to an island's area being finite whereas its shoreline is --- practically --- infinite?
Correct.
You can do a similar 'proof' that Pi is 4 !
You draw a square with a circle inside so the diameter=side length.
You start adding smaller squares into the parts of the original touching the circumference.
Each division is redivided ad nauseam until we have a zig-zag star-like 'polygon' that approximates to the circle's circumference.
Since we know that the circle's circumference is PiD the perimeter of the 'polygon' should be approaching this as we made it progressively nearer and nearer a circle - after all the area of the circle and the 'shrinking' polygon will surely be 'converging' ?
But the cruncher is just like the 'steps' - the perimeter of the 'polygon' is always 4D - so Pi=~4 doh!
Although the areas get nearer and nearer they never match and the perimeters never converge at all ! -
That's if you define π by the circle's circumfence (2×r×π), but what if you define it by its area (r²×π) and sum up infinitely small squares?
How can we know that a dimension that we try to measure could not be defined in any alternative way, leading to a completely different result?
-
@tig said:
practical purposes
I would suggest that here is the nub of the problem.
Geometry is a only theoretical model for the shapes we find in the world around us. Just as Newtonian physics breaks down at velocities beyond our ability to comprehend, so using pure geometry on practical materials has an inherent "bandwidth" beyond which its axioms cannot be applied.
The steps never converge on the straight line because they do not have to exist at an arbitrary, humanly intuitive scale - nor be constructed of the physical units of the real universe (atoms, molecules etc.) Hence my fractal analogy - as purely abstract entities, the steps retain their geometric properties no matter how small we make them, because there is no absolute measure of "smallness" in pure unit-less geometry, only the relative scale of the parts of a form.
In reality, the carpet analogy breaks down at some point where the thickness of carpet, and minimum bend radius, grossly exceed the size of the steps. So it is a category error - we are applying an abstract mathematical theory in a situation where its axioms are not valid.
That is a valuable lesson that is all too rarely taught in school science etc. For example, the inverse square rule applied to the intensity of light, sound, gravity etc, is often used blindly - but the light intensity from a strip light within a room does not follow this, because the assumption of a point-source is broken. -
I just heard a lecture, where a philosopher used a similar analogy with food.
If you take your portion of food and split it in half, and then that portion in half, and on and on, then theoretically you will never be without food. -
TIG
Like in any scientific endeavor you must prove your assertion is valid for all cases and not the special one you selected. Do you have that??You differential must be dl such that integration equals the length and not what you are doing.Read my above post. -
Mac1
What makes you think this is a scientific endeavor ?

All science 'generalizes from the particular', although it pretends it doesn't - all experiment is 'particular', from this a general theory is developed - you can never measure everything so you must rely on a limited set of data from which you generalize into a theory.
I'm not doing calculus here, perhaps you misconstrue me.
I simply made a comparison - calculus relies on making things smaller and smaller and summing them to get a correct result - it works; whereas making steps like this smaller and smaller has no effect because the total length doesn't change - and so it doesn't work!I actually like weirdness of the circle and the zig-zag polygon thought-experiment... that enclosing square gets more and more 'steppy' as it shrinks down into the polygon until its areas is almost that of the circle - it can never equal the circle's area, BUT it will become practically the same... BUT the circle's circumference is fixed at PiD, while the polygon's circumference is always 4D.
My observation is simply this: the areas do converge [but never quite match], but the circumferences are always set in that fixed relationship - the polygon's being ~40% longer than the circle's - although the enclosed areas converge and the 'apparent' forms of both is effectively almost equal 'in practice' - so an almost-equality with a disproportionately divergence of lengths...I fully understand the 'fallaciousness' of these arguments I have set out, by the way

But they show how the very large and very small produce unexpected results - divorced from 'reality' and what you might suppose will happen, when at first applying little thought... -
No, I don't understand what your point is. Why are you using the pythagorean theorem in the beginning of your argument if it doesn't have anything to do with it? What exactly is your argument? The step lines are not always two units long - in your example, where the original triangle was 1meter x 1meter (and the unit being a meter), when you divided it with 2 "steps" the step sides where 1/2 meter, not 2 meters. And when you divided THAT again by half (4 "steps"), the step sides where 1/4 meter. Also, your argument wouldn't work for a right triangle of unegual legs; for a 3-4-5 right triangle, no mater how you divide it, the sides will always have 3 to 4 proportions.
-
I am not using the Pythagorean theorem at all, just stating the general knowledge 'fact' that a right angled triangle with sides of 1 has a hypotenuse of sqrt(2) ~1.414..
If you add the other two edges to make a square these are 1 x 2 = 2.
If you subdivide these you get more but smaller pieces...
1/2 x 4 = 2
1/4 x 8 = 2
1/8 x 16 = 2
etc
So however many bits you make the zig-zag steps out of the total length of the parts is always going to be 2.
When the stepped part effectively overlays the hypotenuse its length is still 2.
Therefore it's ~40% longer than the apparent line it's 'covering'...You are right in that when the steps are divided the previous length 1 becomes 1/2, BUT instead on there being 2 of them like there was before the division, there are 4 so the total length is constant.
It's easiest to see with a 'square' triangle, but in fact the process does work for non-equal sided triangles, it's just that the steps are made smaller in proportions and you need to work out each in separately and recombine. The % discrepancy reduces, the square is the worst case, but the stepped version is still longer than the hypotenuse, even when the edges are tiny and the two practically overlay.
Lets take a 3/4/5 triangle - where we know the hypotenuse is 5 !
Draw in the other two edges to make a rectangle [not a square this time].
These are 3 and 4 long.
3+4 = 7
divide them by 2
(3/2 + 4/2) x 2 = 7
divide again
(3/4 + 4/4) x 4 = 7
Therefore the zigzag is always 7 units long, not the hypotenuse's 5 units. -
@tig said:
Mac1
What makes you think this is a scientific endeavor ?

< I agree it is obviously not an scientific endeavor>All science 'generalizes from the particular', although it pretends it doesn't - all experiment is 'particular', from this a general theory is developed - you can never measure everything so you must rely on a limited set of data from which you generalize into a theory.
<Not really. Look at cosmology and Einstein. They will start form a postulated theory and then prove it. You make an assertion and get a result that is strangely exactly equal to the sum of the two sides. Hum I would be questioning what I am doing? You should be willing to try a different triangle and compare results?>I'm not doing calculus here, perhaps you misconstrue me.
< Not at all I understand calculus but also under stand infinite sum is the path to integration>
I simply made a comparison - calculus relies on making things smaller and smaller and summing them to get a correct result - it works; whereas making steps like this smaller and smaller has no effect because the total length doesn't change - and so it doesn't work!
< Exactly. You are mixing apples and oranges , the sum of the two sides and trying to relate that to the length . Form the differential for the real length and then compare what you are doing. I guess I would conclude: If I am doing it wrong and concluding it doesn't work would not surprise meI actually like weirdness of the circle and the zig-zag polygon thought-experiment... that enclosing square gets more and more 'steppy' as it shrinks down into the polygon until its areas is almost that of the circle - it can never equal the circle's area, BUT it will become practically the same... BUT the circle's circumference is fixed at PiD, while the polygon's circumference is always 4D.
My observation is simply this: the areas do converge [but never quite match], but the circumferences are always set in that fixed relationship - the polygon's being ~40% longer than the circle's - although the enclosed areas converge and the 'apparent' forms of both is effectively almost equal 'in practice' - so an almost-equality with a disproportionately divergence of lengths...I fully understand the 'fallaciousness' of these arguments I have set out, by the way

But they show how the very large and very small produce unexpected results - divorced from 'reality' and what you might suppose will happen, when at first applying little thought...< Just shows we are not omnipotent. IE quantum mechanics vs wave equations >
-
My brain just exploded
-
Zeno's paradoxes.
http://en.wikipedia.org/wiki/Zeno%27s_paradoxes -
so. .. Pythagoras isn't wrong???
-
@tig said:
I fully understand the 'fallaciousness' of these arguments I have set out, by the way
Never doubted it for a second!

@tig said:
But they show how the very large and very small produce unexpected results - divorced from 'reality' and what you might suppose will happen, when at first applying little thought...
Your Rubies do things that would have made Pythagorus' brain explode. "Unexpected" results, hmmm, now that I do find hard to believe!

But you're quite right, jumbling theory and reality in these kind of thought experiments really can be fascinating - and has a long history of provoking the insights that push science and mathematics forward.
PS) Anyone got a pet carrier and a geiger counter I could borrow?...

Advertisement







