[Tip] Calculate pixel width needed for a good-looking print
-
For magazines, newspapers, etc, you need this width in pixels:

For road billboards, you need this width in pixels:
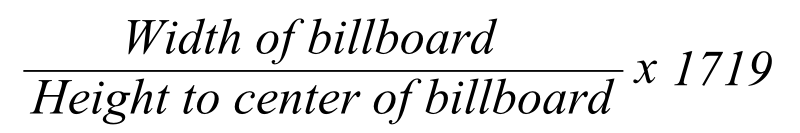
And that's it. It doesn't matter what units you use as long as it's the same units both up and down. You should subtract the average Eye Height in your country from "Height to center of Billboard" before using the value in the formula.
Examples of application:
For a magazine with a width of 20cm:
You need a photorealistic render of a house spanning the full page width. Hold the magazine as you normally would when you see an image like that, and measure the distance from your eyes to the paper. It might be 35cm, so then you need 20/35x3438 = 1964 pixels width for your render.
Now let's say it's an assembly illustration, one that shows every last bolt with superimposed text. An image like that is likely to be more closely examined, so let's say most people will look at it from 25cm (I measured myself). This means you need 20/25x3438 = 2750 pixels width.
For a 2m x 1m poster:
If a single photorealistic image will use up the full poster, then most people will stand 2m away from it to appreciate it (This also depends on space constrains in the venue, of course). Then you need: 2/2x3438 = 3438 pixels width for this render.
On the other hand, if we're talking a bout a mixture of text and working drawings, the poster will obviously be examined more closely, around 70cm distance. Then the poster needs 200/70x3438 = 9822 pixels width to look good.
Now a 8m x 4m billboard in the road:
A 8m-width billboard with its center at a height of 10m, only needs 1652 pixels in width to look good... (8/(10-1.676))x3438 = 1652. (I used SketchUp's default eye height here)
If you want further explanation on how I came up with these, just let me know.
-
Looks like I'm the only nerd who wants to know the details of how you figured this out

Matt
-
@Matt
No, I also find this info useful for work I do.
I so signage for conventions and stuff. This helps greatly. -
@Artistram3d1 - Interesting that you said that, I just heard back from someone who is hiring me to signage and rendering for trade show booths. Got a couple questions for you.
- Do you have any tips or tricks for signage and the like?
- Do you do renderings of the signage? If so, then what renderer do you use?
That all said, thanks @Ecuadorian for the info on how to set this up. Once I go through this enough to feel confidant on this I might sketchup some diagrams to add a visual to the explanation as well (I'm more of a visual learner), as that always helps.
Thanks!
-
Hello.
Now that I see both formulas again after a while, I'll leave the first one stay as it is, but the second one needs a correction. Instead of "Height to center of billboard" it should rather be "Height to bottom of billboard minus eye height". Eye height is usually considered to be 5'6", or 1.68m. The change is because I did not consider the following to be too important before:
- That for smaller billboards, the height of the observer IS important
- That althought the center of a billboard might look sharp, the lower part, which is closer to the observer, might not look as good.
I wrote (for another forum) an explanation in Spanish for the logic behind the first formula. I'll translate it here:
According to John Russ (The image processing handbook, 2006) "The upper limit (finest detail) visible with the human eye is about 50 cycles per degree...". This means normal vision can resolve two lines separated 1.2 arcminutes (60/50).
Then, when you have a pixel density so that every pixel occupies 1 arcminute in your visual field, you no longer see individual pixels, but a continuos image.
From there I simply calculated the proportion between the physical size of a pixel measuring one arcminute in your visual field and the distance from your eye to that pixel. That's what the Tangent trigonometric function is for, to give us the proportion between the side opposite to the angle and the side next to the angle. So I calculated the Tangent of one arcminute... Tan (1/60). This means for any distance from eye to printed media, the size of each pixel must be 0.0029088821687 times that distance (Tan (1/60)) to form a continuos image.
Now, the size of each pixel in a print can also be expressed as (Image width / amount of pixels in that width). Actually, the same could be said about the height... I could make the formula more abstract and just say "dimension", but I settled for "width".
We now have two formulas, both equal to "pixel width". Let's put them one next to the other...
Pixel size to see a continuous image = Tan (1/60) * distance from eye to print
Physical pixel size in a print = Print width / width in pixelsWe want pixels in our prints to form a continuous image, so...
Pixel size to see a continuous image = Physical pixel size in a print
Ant then...
Tan (1/60) * distance = Print width / Width in pixels
Width in pixels * Tan (1/60) * distance = Print width
Width in pixels = Print width / (Tan (1/60) * distance)
As we saw before, the Tangent function of 1/60 is a very small value full of decimals spaces, so to keep it all "clean", we'll use the reverse of that...
Width in pixels = (1/Tan (1/60)) * (Print width / distance)
With any scientific calculator we see that (1/Tan (1/60)) equals 3437.74667..., so:
Width in pixels = 3438 * (Print width / distance)
And that's it. When I feel like doing so, I'll explain the second formula...
-


-
so it's one practical, everyday use of the Rayleigh Criterion. thanks for calculating this for us

-
very useful and informative tips and tricks.thanks for sharing.

Advertisement







