Défi - Octaèdre

SERGIO

Hello!
Voilà une méthode sans calcul.
J' ai bon?
Sergio

Hoho !!
J'avais pas vu le fciheir octaedre facile de Jean
c'est du même genre
Mais ça n'a pas la classe du ficheir octaèdre ultra facile

REGIS

Bon

il y a eu plein de réponses pendant que je planchai mais bon je poste mon idée et je verrai après si elle a été proposée.
J'ai fait dans le simpliste :

Dessiner un carré de 100 de côté
Tracer une ligne sur l'axe bleu au centre du carré
Tracer une ligne guide avec l'outil mètre en partant d'un coin du carré et en rejoignant la ligne guide au centre du carré en s'assurant que cette nouvelle ligne guide fait 100.
Il n'y a plus qu'à relier tous les coins du carré avec le point trouvé sur l'axe central du carré et faire une copie pour la deuxième partie de l'octahedre.
Essai octahedre.skp

@+

vick

Une autre formule
Un carré de 100 x 100
Je l'extrude de 70.7 en hauteur ( pour être précis)
avec l'outil mise à l'échelle je reduit la face de dessus a zéro.
la partie haute est réalisée.
Partie basse idem,la face de dessous reste visible.

pilou

@Vick
Malin
Dans la première version comment "tirais-tu" les sommets?
Et avec quelle version de SU?

vick

SU 7

Avec l'outil déplacer, je pointe sur le croisement des 2 diagonales , je bloque l'inference bleu et je tire vers le haut.

pilou

@Vick
Encore un de ces mystères
ça ne marchait pas hier, et ça marche aujourd'hui
(il faut évidemment dans la 6 intersecter tout le bazar avant de monter les diagonales)

Ricco

Tirer sur l'intersection, c'est ce que je disais cette nuit, mais la face disparait, et dans le modèle de Vick, en fait il faut retracer les diagonales ou copier et miroir , sinon, comment faire ?
ricco

SERGIO

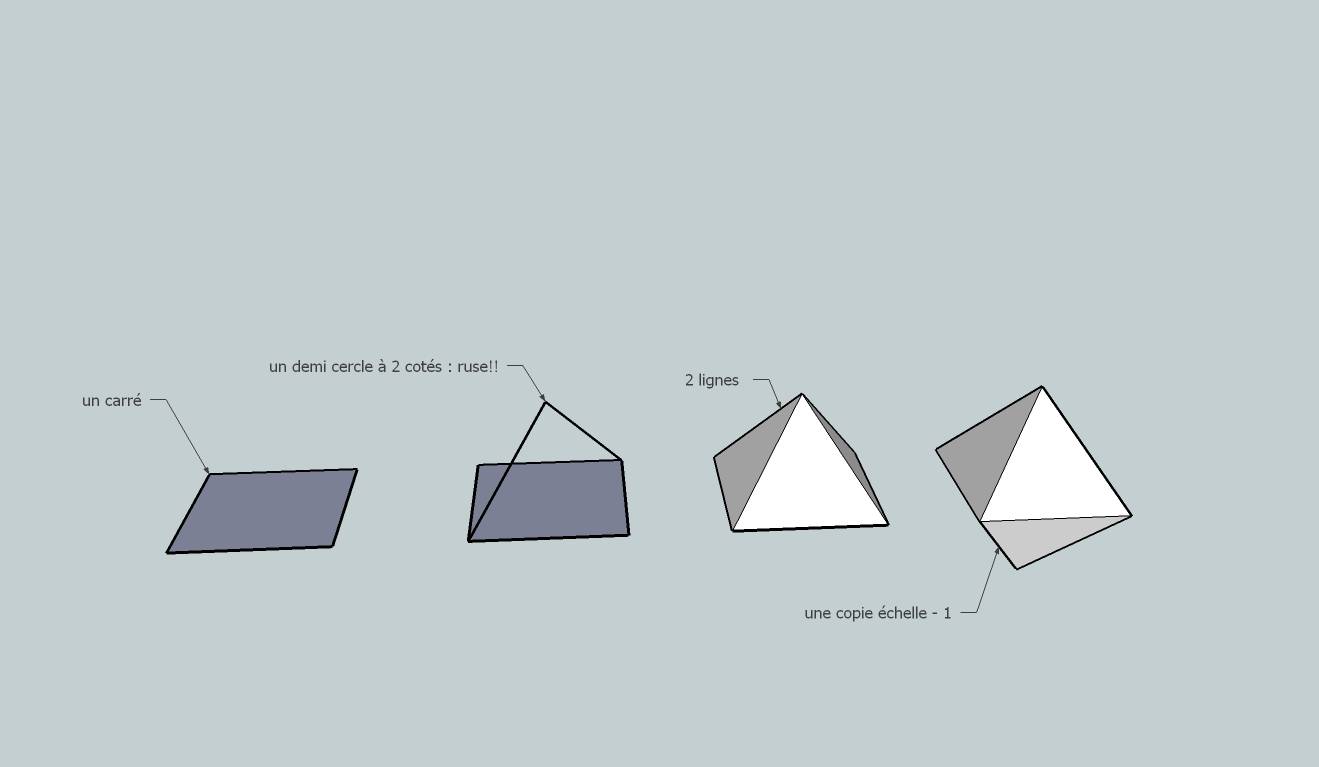
Encore plus simple et toujours sans calcul!! Octaèdre 2.jpg

Jean Lemire

Bonjour.

@unknownuser said:

Hello!
Voilà une méthode sans calcul.
J' ai bon?
Sergio

Excellent, une autre méthode à retenir: positionner des géométries et s'en servir pour en pivoter d'autres.

Merci Sergio.

Salutations.

Jean Lemire

Bonjour Régis

@regis said:

Bon

il y a eu plein de réponses pendant que je planchai mais bon je poste mon idée et je verrai après si elle a été proposée.
J'ai fait dans le simpliste :

Dessiner un carré de 100 de côté

Tracer une ligne sur l'axe bleu au centre du carré

Tracer une ligne guide avec l'outil mètre en partant d'un coin du carré et en rejoignant la ligne guide au centre du carré en s'assurant que cette nouvelle ligne guide fait 100.

Il n'y a plus qu'à relier tous les coins du carré avec le point trouvé sur l'axe central du carré et faire une copie pour la deuxième partie de l'octahedre.
[attachment=0:371t369f]Essai octahedre.skp[/attachment:371t369f]

@+

Ta ligne guide fait 99,992536 au lieu de 100. Mais l'idée est bonne. Il s'agit de trouver une manipulation pour obtenir cette ligne à précisément 100.

Merci et salutations.

Jean Lemire

Bonjour Vick.

Tu mentionne ce facteur:

@vick said:

Une autre formule
Un carré de 100 x 100
Je l'extrude de 70.7 en hauteur ( pour être précis)
avec l'outil mise à l'échelle je reduit la face de dessus a zéro.
la partie haute est réalisée.
Partie basse idem,la face de dessous reste visible.

En fait pour être vraiment précis, il faut prendre :

100 * 0,70710678118654752440084436210485 = 70,70710678...etc.....

et encore, ce n'est pas totalement exact.

Pour les curieux, 0,707..etc.. c'est le sinus de 45°.

Salutations.

Jean Lemire

Bonjour Sergio.

@unknownuser said:

Encore plus simple et toujours sans calcul!! [attachment=0:2ab6w71g]Octaèdre 2.jpg[/attachment:2ab6w71g]

Impeccable.

Salutations.

vick

Bravo Sergio:

pilou

@Sergio
Encore une bonne solution celle-là!
Par contre la copie + echelle -1 demande 2 fonctions distinctes, alors que la "copie rotation"
une seule du fait qu'on peut faire CTRL pendant la rotation

Une des ruse pour faire une rotation d'un volume perpendiculaire à une des ses base, est d'aller piquer l'orientation sur un des axe de l'origine, de le bloquer avec Shift, et de faire enfin Ctrl pour la copie ouf

pilou

@unknownuser said:

Pour les curieux, 0,707..etc.. c'est le sinus de 45°.

ou (racine de 2) / 2

Jean Lemire

Bonjour Pilou.

Exact.

Salutation.

pilou

Oui, c'est gràce à ces petits défis que j'ai redécouverts cette fameuse racine de 2
Quand on la manipule "concrètement", on comprend mieux ce qui se passe!

Evidemment tout vient de ma petite manipulation des triangles du départ et du fameux théorème de Pythagore
qui dit que dans un triangle rectangle le carré du côté opposé à l'angle droit (l'hypothénuse) est égale à la somme des carrés des côtés de cet angle droit!

Comme mes côtés faisaient "1" on a 1² + 1² = x² soit 2 = x² soit x= racine de 2 soit 1.41421...

Que je n'ai évidemment pas eu à calculer, c'est SU qui s'y est collé, quand j'ai tracé le segment rejoignant les 2 côtés

Un autre triangle rectangle remarquable 3,4,5 que les bâtisseurs de cathédrales connaissaient bien pour faire des équerres et que tout soit d'aplomb

Ma méthode est plus précise (relativement) que celles qui demande de faire "monter" ou bouger d'une certaine valeur

Ricco

je dois dire que le demi cercle à deux côtés, segments en fait , c'est assez redoutable, très joli coup, on est vraiment dans l'antichambre privée des " Tip & tricks " de SU.
Remarquable
ric.

Jean Lemire

Bonjour Ricco.

Exact, ces Tips & Tricks ou Trucs et Astuces, il y en a pas mal et certains peuvent être d'une grande utilité.

Voir le fichier suivant pour un truc avec les lignes de cotes. Dans ce fichier j'utilise une ligne de cote pour expliquer que les deux objets doivent êtres alignés d'une certain façon. Une ligne de cote me fourni un contenant superbe avec une place pour du texte et deux extrémités féchées pour pointer vers ce que je veux montrer.

Trucs avec les cotes.skp
La scène 1 montre le résultat et la scène 2 montre les explications.

Le tour de passe-passe du triple click est moins évident. En effet, avec une cote normale, vous positionnez la fin sur une géométrie avec un click, puis vous tirez la cote de côté et cela génère deux lignes de rappel et la ligne de cote elle-même. Vous complétez avec un dernier click, ça fait donc deux clics pour terminer la cote. Je me suis dit: qu'est-ce qui arrive si je clique deux fois de suite sur le point d'arrivée ? Je devrais ne pas avoir de ligne de rappel et avoir la ligne de cote alignée entre les points de départ et d'arrivée. Et bien non, ça ne fonctionne pas toujours. Avec trois clics, pas de problème. Attention il faut légèrement espacer les clics (environ une demi seconde entre chaque) de façon à aller plus lentement que la vitesse de votre double clic si vous voulez que SU enregistre bel et bien des clics.

Salutations.

Ricco

On va tout savoir
Je vais bien potasser ton truc, j'ai souvent ce pb d'aligner des éléments, " aligner " ne me semble pas simple, j'ai pas eu le courage de potasser tout le mode d'emploi, en fait
Sinon, comment peut on trouver le truc des cotes sans lignes de rappel, c'est écrit où ?
Jamais entendu parler, ou lu ?
Bon, tout ça se bouscule, et pour quelqu'un comme moi qui a le " cerveau lent..."
Car je teste toujours derrière, SU c'est comme la danse, on n'apprend pas que dans la tête mais aussi sur la piste, là, il faut exécuter, dessiner !
A+
Ricco