Center point of a circle
-
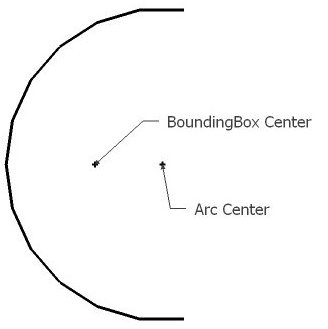
It's important to understand the method used by the script for finding the centerpoint. It creates a BoundingBox around the selected entities, and the centerpoint is the center of the BoundingBox.
For a circle, this centerpoint happens to be the centerpoint of the circle. This is not true for an arc, or other non-symmetrical 3d objects.
-
Dear All,
The inferencing method to find the centre only works if the circle is unexploded, which is not always the case. Very often I need to find the centre of a circle that has somehow lost its circle entity status. Using weld.rb to rejoin all the segments doesn't work as the entity status changes from 'circle' to 'curve', and inferencing won't work. Usually, I draw two temporary diagonals and then place a construction point at the intersection.
Here is a suggestion for a ruby:
- call it curve_centre.rb,
- select three (3) consecutive end-points (two adjoining line entities), and voila,
- a construction point magically appears at the intersection of the mid-point normals.
Has anyone come across such a ruby?
Regards,
Bob -
watkins,
I started some code to find the center of an arc from line segments. My method used some calculations to find the bulge., but I like your idea - it's easier to write. Actually, you would need only 2 segments, right?
-
Dear Jim,
Yes, the method could be made to work with only two adjacent line segments. The method would also be independent of the number of line segments making up the arc or circle provided that all the mid-point normals past through the same point in space.
Bob
-
Hi folks.
I know it is obvious but just in case.
With exploded circles and arcs, you can use this procedure:
1 - Draw the perpendicular from the midpoint of two adjacent segments. TWo lines to draw.
2 - Their intersection point is the center of the circle.
Just ideas.
-
Actually, yes. You can draw a 2-segment arc over top of any 2 segments, then use the Point at Center option...
-
I know this a rather old thread, but I thought it worth bringing it to the surface for those (like me) who didn't know. Finding the centre of a circle or curve often seems difficult. I've been using the inference technique, but it doesn't always work easily, so I did some searching & arrived here.
And yes, provided Windows>Preferences>Extensions>RubyScript Examples is checked... then you can context click the circle or curve and 'Point to centre'. Hurrah! another gem discovered!
-
@jean lemire said:
With exploded circles and arcs, you can use this procedure:
1 - Draw the perpendicular from the midpoint of two adjacent segments. TWo lines to draw.
2 - Their intersection point is the center of the circle.
Just ideas.
Nice tip, Jean. I guess they do not have to be adjacent, even.
-
A little icing on the cake, if you want a plugin:
Chris Fullmer's Exploded Arc Centerpoint Finder. Places a C point where the center of a fragmented arc or circle is supposed to be. -
Thanks, Tim. I can use that one, which I guess uses Jean's method to do the job quicker.
I admire Jean for apparently eschewing the way of methods outside of the native tools as they tend to cloak the logic of the underlying operation, and thus may in some sense be debilitating.
What? Long live the plugin. Long live Jean. Shut up, Brooke.
-
Jean Lemire is one of the most helpful people in this forum. His posts are always enlightening. Thank you, Jean Lemire.
Advertisement







