A la recherche du quadrilatère(s) perdu(s)!
-
" Elles sont déjà toutes "Planes"!
"C'est le cas, difficile de couvrir un toit gauche
-
Ah oui, j'en vois plus mais toujours pas de surface gauche de départ!
@unknownuser said:
C'est le cas, difficile de couvrir un toit gauche
Oui, mais c'était l'hypothèse de départ!
(il y a plein d'exemples à charger sur les pages précédentes pour se faire les dents (de la mer) La plupart des surfaces générées par exemple par the Extrude Tools de TIG fournissent des structures Gauches!
Ainsi que les serres faites à la va-vite par le Patrick!
D'où le casse-tête de l'été : comment rendre toutes ces facettes "gauches" de structures... "Planes" !
Et y coller au plus près (accessoirement) -
Par exemple ici tous les rectangles sont "gauches" mais magiquement le fait de joindre leurs milieux donnent des losanges "Plans"
(touvé ça totalement par hasard)
Et ainsi l'orientation d'un vitrage par exemple!
Le but du jeu est maintenant de faire un bati "plan" itou rectangulaire entourant ces losanges!
Voir mes essais pages précédentes...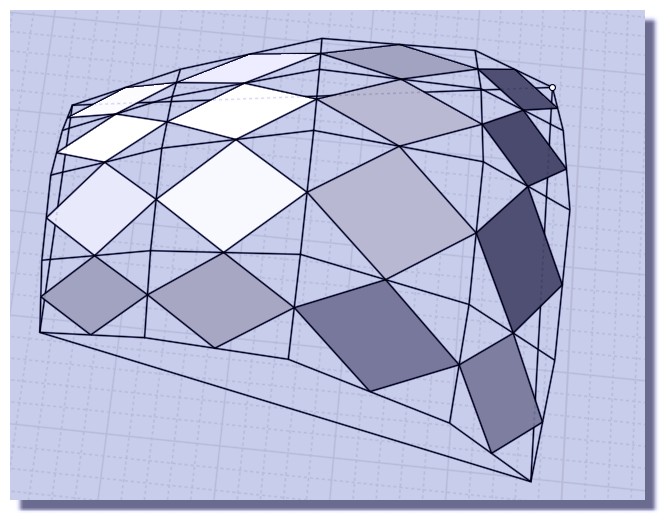
Ici le 1er rang qui semblait prometteur!
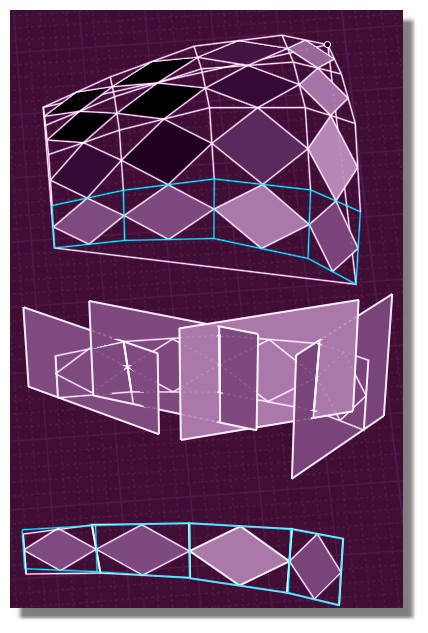
Il faut que je creuse encore...
Bien sûr comme dans les vidéos Rhino montrée plus haut les 2 structures ne seront pas totalement identiques!
On peut se donner des contraintes ...les rives par exemple...PS ça y est je vois l'image de l'os à ronger!
-
perso, l'image de Patrick s'est affichée
...GH, c'est pour Grasshopper
et pour le fichier de Lauferon, yep, c'est tout plat, mais dans l'idée (comme j'ai remis sur l'image) c'est que les guides (epures) a l'arrivée, ont une logique
j'ai complété son fichier ci-apres ... les lignes de fuite ont une logique pour faire des plans
essai_complete.skpd'ou, l'illustration
Tchussss
-
@Pilou C'est vrai que je prends le problème dans l'autre sens.
Pour modifier la forme globale, l'outil de mise à l'échelle est intéressant, sans rendre gauches les surfaces.
@David les charpentiers n'apprécient pas beaucoup les plans gauches sauf ceux de ce type
-
Oui l'outil mise à l'échelle général est très cool...
c'est ce que j'avais montré dès le début!Et si on prend une forme qui a déjà toutes surfaces planes elle va les garder jusqu'au bout de ses transformations génériques!
(mise à l'échelle)Ici une sphère par exemple transformée en ellipse et troncaturée!
Pas besoin de les replanifier...elles le resteront jusqu'à vitam aeternaum! -
@lauferon said:
@David les charpentiers n'apprécient pas beaucoup les plans gauches sauf ceux de ce type
... i am also Carpenter ... mais y a pire, je fais de d'enveloppe ... alors les plans gauches tu sais belle photo, effectivement, j'aime ... et j'ai hâte que tu me dises quel complexe ils ont prévu en couverture
bravo ! ... tu aurais le modèle 3d sous le coude ?
-
Séville ...c'est ondulant mais pas gauche...un sacré bazar encore celui-là!
-
"i am also Carpenter"
" La couverture" Je ne sais pas.
Source photo :" Enttreprise Simonin illustre le savoir-faire français à l’Exposition Universelle de Milan 2015""tu aurais le modèle 3d sous le coude ? Non, désolé.
-
okkkkayyy
Si c'est Simonin, je vois mieux
... belle vitrine et même pas besoin de couverture (ouf!)
Merci pour les photos en tout cas
-
"pilou": Etonnament le fait de joindre les milieux pour faire des losanges génèrent ceux-ci
avec des surfaces planes!Étonnamment, pas tant que ça! il s'agit du théorème de Varignon:
https://debart.pagesperso-orange.fr/college/parallelogramme_translation_classique.htmlPour revenir au problème de départ : je pense qu'il n'y a pas de solution pour remplir une surface gauche comme la serre de Patrick avec des quadrilatères plans, si ce n'est d'absorber les problèmes de jonction par un treillis métallique, comme dans le cas de la serre de Patrick.
j'ai fait quelques essais sur le prototype de Patrick. Ci-dessous le résultat, en conservant la géométrie de départ, j'ai juste corrigé légèrement la base, tous les points n'étaient pas au sol (delta de l'ordre du millimètre).
En utilisant VertexTools de thomthom V2.0. pour rendre plan les faces gauches. J'ai 36 quadrilatères plans les autres restent gauches.
-
Je peux me tromper mais tout ce qui est écrit sur les quadrilatères (concaves, convees, carrés...) sur la page communiquée ne parle que de quadrilataires dessinés dans un plan x,y et non dans l'espace 3D x,y,z? Me trompe-je ?
Ah Varignon le copain comme cochon de Bernouilli...ça nous rajeunit pas!
Déjà au 18 ème siècle la géométrie faisait bouillir les neurones!
Je n'ose imaginer ce qu'ils auraient fait avec les SketchUp et autres Rhinocéros...Et toujours magique que cela marche aussi en 3D!
Effectivement peu de faces planes!
Ma méthode précédente des extrusions le long des arêtes permettrait toutes les facettes planes sauf une à 0.07 unité...mais pénible à la main mais n'auraient pas exactement la même forme générale...
La méthode des losanges va donner que des surfaces planes très peu différentes de la forme de départ!
j'ai encore amélioré la procédure...j'y retourne...Il serait quand même plus facile de faire dès le départ des facettes planes, surtout pour y mettre des vitrages!
-
@pilou said:
Je peux me tromper mais tout ce qui est écrit sur les quadrilatères (concaves, convees, carrés...) sur la page communiquée ne parle que de quadrilataires dessinés dans un plan x,y et non dans l'espace 3D x,y,z? Me trompe-je ?
Tu ne te trompes pas. J'ai envoyé le 1er lien qui m'est tombé sous la souris. Mais le théorème reste vrai pour les quadrilatères "gauches".
-
@unknownuser said:
Mais le théorème reste vrai pour les quadrilatères "gauches".
Ce que j'ai redécouvert par pur hasard, 3 siècles après nos illustres prédécesseurs lors de ces vacances hautes en températures!
Corollaires pour la serre du Patrick: on a toute la surface possiblement couverte en verre, un peu plus basse il est vrai, mais avec juste 3 formes modulaires! Mais surtout avec la structure prévue dès le départ sur une nappe de bar!
Bon c'est pas sûr qu'une structure "portante" par dessous soit moins simple qu'une structure portante par dessus!
Ce qui est interessant aussi, quand on pioche toujours le même sujet, c'est que l'on épluche les fonctions des programmes en même temps!
Que l'on trouve (ou pas) des manipes pas croyables...ainsi que des fonctions insoupçonnées!
-
Ah ça c'est rigolo! Encore de la magie!
(j'en ai rempli qu'une bonne moitié...mais tout peut se remplir de la même façon)
Etonnant encore, une structure entièrement gauche soutend une couverture de remplissage entièrement plane!
La structure qui entoure les losanges d'une forme quadrangulaire est complètement gauche!
Le fait de joindre dans un 2ème temps les losanges (qui eux-mêmes étaient devenus plans par la magie de la géométrie) génèrent des rectangles (rouges) qui sont encore une fois tout bonnement plans!
Bon les triangles c'est plus facile, car je ne connais pas de triangle gauche!
Les 2 petits triangles bleus au-dessus d'une arête d'un rectangle rouge sont en une seule partie...
Les triangles verts de rives sont en 2 parties! (ou pas) Ils sont à l'endroit de la "brisure"(sauf les 4 coins de la base)Du coup on peut vitrer toute la surface sans problème et on garde intégralement la structure de départ faite à la va-comme-je-te-pousse!
Etonnant non ?
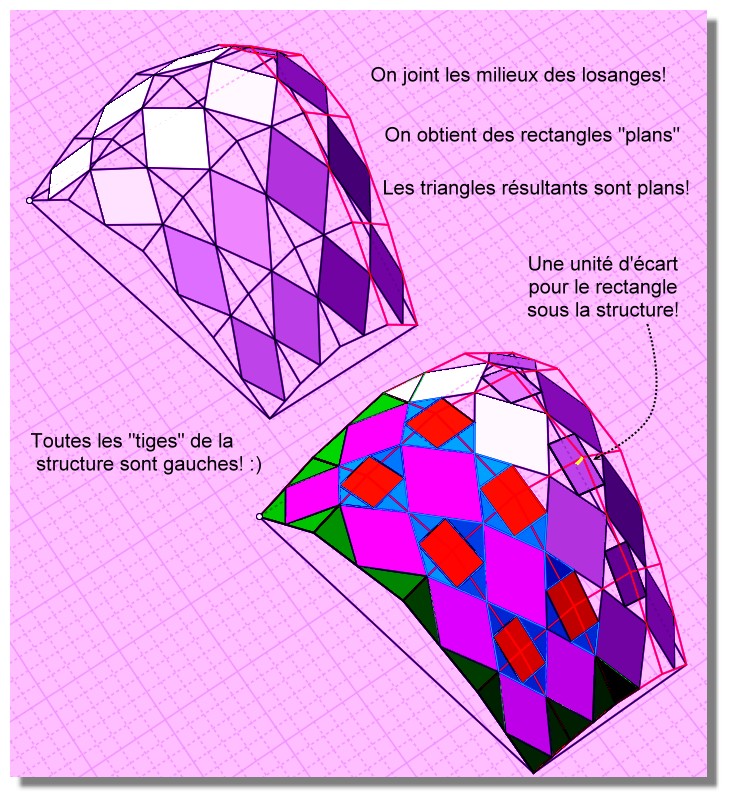
Les triangles "noirs" sont en fait des triangles verts dans l'ombre!
La distance hors tout de la plus grande longueur au sol de la structure fait 22 unités...
La plus grande distance de "décollage" de la structure qui se trouve au-dessus d'un rectangle rouge fait une unité...Il n'y a que 3 niveaux de remplissage...pas mal pour des surfaces foireuses!
Ci-joint un SKP... loin d'être rempli!
-
Problème associé pour fin de vacances en roues libres!
Existe-t-il toujours un point P(x,y,z) dans l'espace formant 4 plans P1, P2, P3, P4 d'après les 8 sommets donnés A,B,C,D,E,F,G,H dans l'espace 3D ?
Et accessoirement comment le trouver ?
-
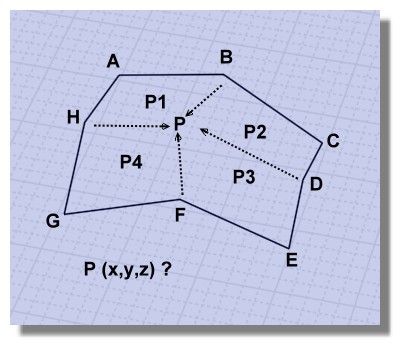
Toutes les intuitions sont les bienvenues!
Faire l'intersection de 3 plans c'est de la rigolade, mais 4...ça calme de suite!
Quelle est la suite de la procédure ?
On prend le milieu du segment d'intersection et on reteste avec les 4 côtés?
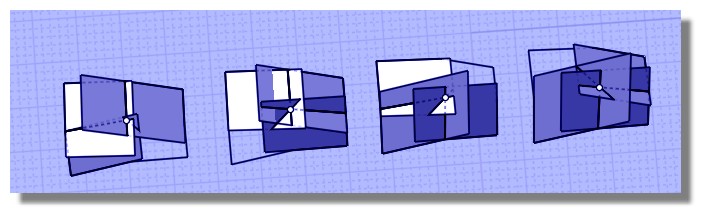
Là j'ai tenté l'intersections de "3 plans tournants" de garder les 4 sommets résultants
d'en bricoler une moyenne, un centre de gravité, mediatrice, médiane, centre d'un cercle etc... mais pas encore concluant!
-
-
lol
J'allais te faire un escroquerie ... et je vois que c'est toi l'escroc qui a réédité ton post
bon, j'enchaine malgré tout ...
pour croiser mes 4 plans c'etait easy ... mais ça donnait ce que j'ai mis dans le précédent post ...
du coups ... PLOUF pour 4 quad perfectmaintenant si tu souhaites une fin heureuse ... tu ouvres ce nouveau fichier
... et tu ne cliques surtout pas sur la "balise 0" pour garder la magie de ce beau moment (et oui, tout fout le camp, on dit balise maintenant
...tchuss
-
Semblait séduisant mais...
J'ai tout repris, éclaté, pris un repère que je replace sur le fichier original
Je n'arrive à faire que 3 faces planes! (alors que dans l'essai cela semble marcher visuellement)
C'est sûr ça doit pas passer loin!
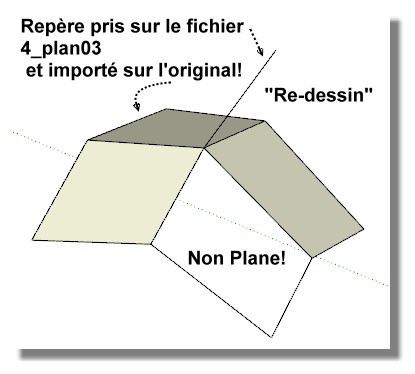
Il serait intéressant de savoir la procédure employée...
Le secret serait dans cette construction ?
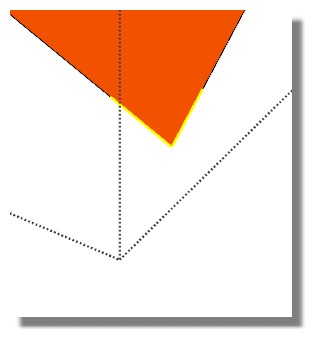
Advertisement