Line length on circle scaled to ellipse is very wrong
-
I'm sure this has not been a problem in the past, I need the length of the line that forms the ellipse. At first I thought it was to do with number of segments and as you can see, it does, but not in a good way.
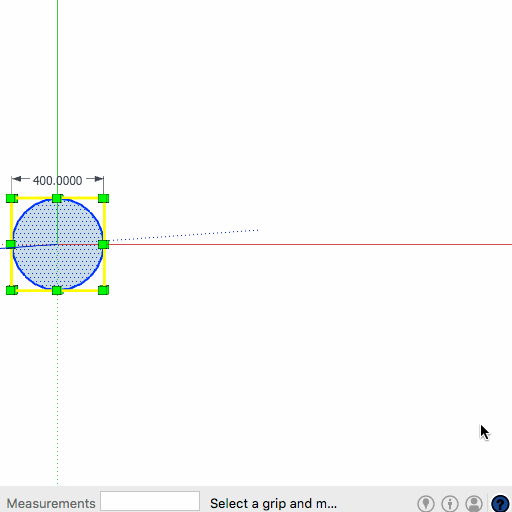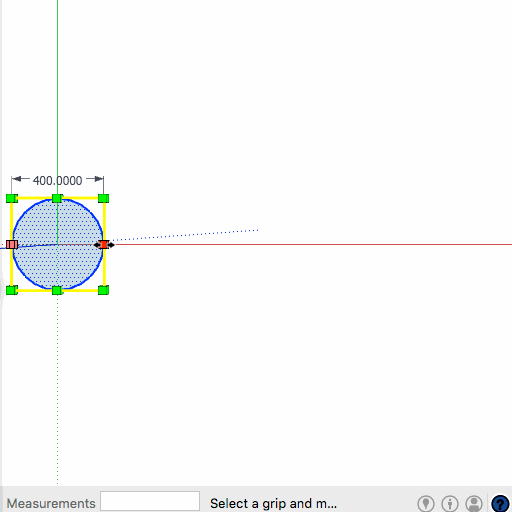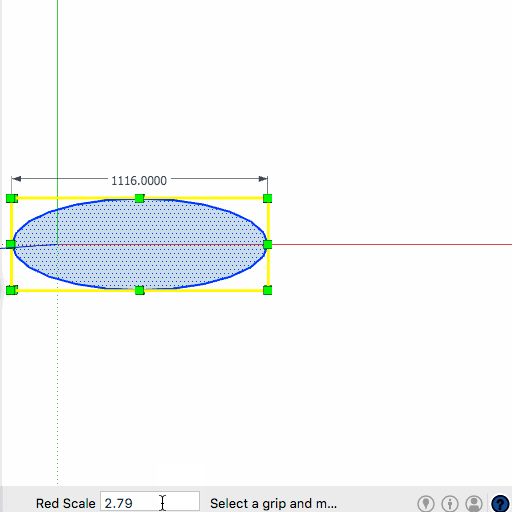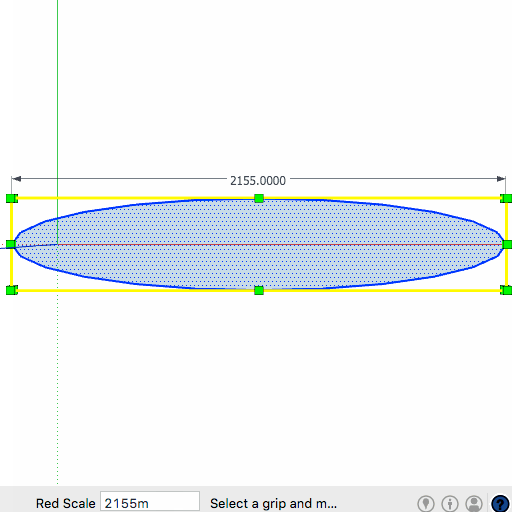
Ellipse was formed by scaling a 400mm Diam circle, scaling in one direction and entering 900mm.Tried exploding and welding and quartering and whatnot but...
I'm hoping this doesn't turn out to be a 'Duh'.
(The actual line length is 2155 +/- 5. measured in the real world).
Puzzled Baz
-
not sure I follow you explanation, do want the end length to equal 2155m [or whatever units]...
john -
Hi John. I am wrapping these columns with ply and veneer. I was hoping to get an accurate length...IE: the line length of the ellipse.
-
I figured you meant the circumference/curve length [after I posted]...
the number of segments will affect the returned length as SU is Edges...
'Entity Info' update on 'Left Button Up' so you can get pretty close if you watch it as you scale...
when you get close use the VCB to up scale marginally e.g 1.000673
with 2000 sides you want to scale too 676.4085...
however, number of edges needed really depends on the thickness and mailability of your ply...
for a veneer 2000 should be ample...
john
-
I have a given ellipse with a minor of 400 and a major of 900.
Why do you suppose different segments give such different answers, none of which is accurate anyway. -
in SU any curve is a sequence of edges, each Edge has a fixed length, added together they equal X...
X = number of edges times edge length...
the more edges the longer the distance needed to complete the path...
if you have a 2155mm edge curve made up of 2155 edges, each 1mm in length, than that's better than most people can cut manually...
if you export to cnc as a dxf, than even 24 edges will be fine if the chord lengths are correct mathematically...
it is called Sketch Up after all...
john
-
If you export the ellipse as a 3d model to .dxf you should get the correct circumference.
-
Thanks Box.
John, I understand about the segments adding up. But it seems as if SU doesn't like lines which have been scaled. And I'm not seeing this with arcs, regardless of number of segments the line length remains the same.
However, will chuck that one in the too hard basket for the time being,
Thanks for your help. -
@baz said:
I have a given ellipse with a minor of 400 and a major of 900.
Why do you suppose different segments give such different answers, none of which is accurate anyway.Several perimeter of ellipse approximations can be found here
https://www.mathsisfun.com/geometry/ellipse-perimeter.htmlUsing Approximation 2, the perimeter would be 2118.265712279433
mnr=200;mjr=450#semi-minor and major axes cir=(Math;;PI*(3*(mjr+mnr)-Math;;sqrt((3*mjr+mnr)*(mjr+3*mnr)))) -
Wow, this is getting complicated.
-
if you split the circles before the length of the two half curves remains the same when scaled regardless of sides...
-
@pbacot said:
if you split the circles before the length of the two half curves remains the same when scaled regardless of sides...
Sorry, not quite following you there.
But to restate the question: If I draw a line at 100, Entity Info will tell me its 100.
If I draw an arc and explode, I will get an accurate line length.
However, if I scale a circle to make an ellipse, Entity Info gives me nonsense, and not even consistent nonsense. I just went back to my example model as shown at top and all the reported numbers are now different...It's to do with scaling, I reckon. It confuses SU's little brain.
-
This might be a bug..
-
@ely862me said:
This might be a bug..
According to previous posters, it is a limitation of SU. But I can't see why a line shouldn't be a line, whether curved, stretched or otherwise abused.
Shall I load the skp? -
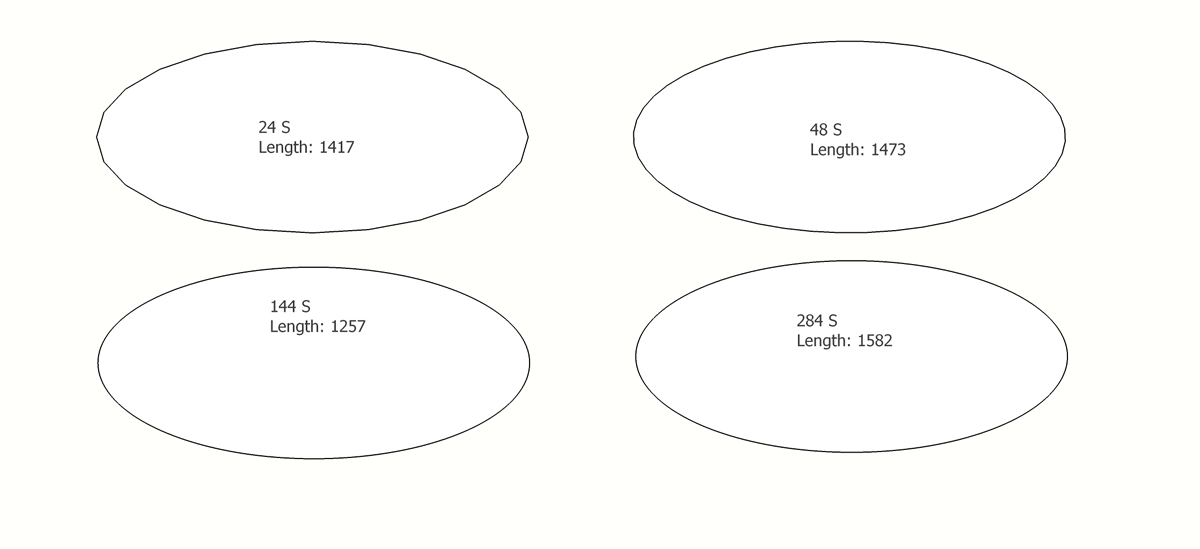
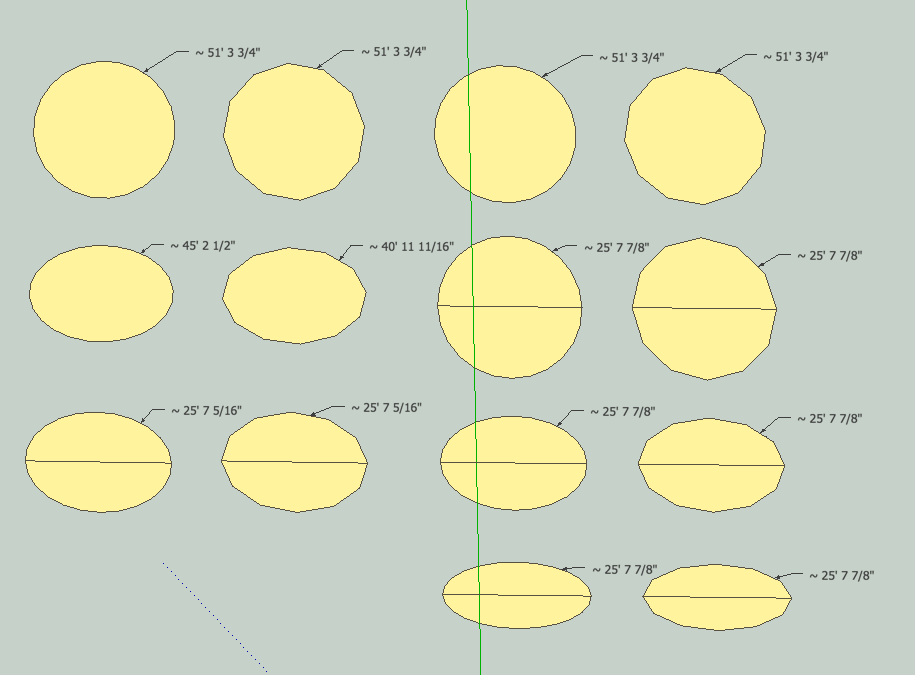
Circle1 144s at 400 mm - scale by factor of 2
Circle2 288s at 400 mm - scale by factor of 2entity information reports ~5026.5 mm for both - I don't know where this number comes from
Then pushpull each ellipse into elliptical cylinder
Select arc and explode
entity information now reports ~3872.6 mm for Circle1
entity information now reports ~3875.3 mm for Circle2Elliptical Circumference calculates out at 3875.38
-
@garry k said:
Circle1 144s at 400 mm - scale by factor of 2
Circle2 288s at 400 mm - scale by factor of 2entity information reports ~5026.5 mm for both - I don't know where this number comes from
Exactly! Or inexactly as it happens. Could you open that file again and see if the numbers have changed, they have on mine.
-
Once you get to copy them around you get all kinds of lengths.
-
@baz said:
@pbacot said:
if you split the circles before the length of the two half curves remains the same when scaled regardless of sides...
Sorry, not quite following you there.
But to restate the question: If I draw a line at 100, Entity Info will tell me its 100.
If I draw an arc and explode, I will get an accurate line length.
However, if I scale a circle to make an ellipse, Entity Info gives me nonsense, and not even consistent nonsense. I just went back to my example model as shown at top and all the reported numbers are now different...It's to do with scaling, I reckon. It confuses SU's little brain.
It doesn't make sense. Really CAD programs should have an ellipse tool.
-
I did some probing via Ruby, and it seems there is a chain of bugs causing this. First, when you scale a circle to make it an ellipse, SketchUp should drop the metadata defining it as a circle and treat it as just a closed loop of segments (a Curve). It does not do so, it continues to carry the center point, radius, and normal vector as if the loop is still a circle, and the edges still say they are part of an ArcCurve. This evidently triggers a second bug in the method that calculates the circumference of the loop. In some cases it still calculates the mathematical 2pir as if the circle hasn't been scaled. In other cases it calculates a strange value that has no evident relationship to anything. In no case does it return the sum of the lengths of the edges!
-
Lengths of (part of) an ellips do not show rigtht. This has been mentioned before.
I hope you can see this thread. See posts around 17/4/2008 and on.
https://groups.google.com/forum/#!searchin/sketchup3d/ellips$2Barea%7Csort:relevance/sketchup3d/z70T5xdUm_I/g-ChcSEcL2YJ*"Taff, Google SU team,
Very nice approach Taff, almost precise. Here again there is the
lack of a precise ''snap to" with these rotations. But it's the best
you can do!But I noticed an (important) bug in the "Entity Info" and "Text"
tool output.
The curve length shown is only half of what it should be.Before you exploded the 1/4 ellipse curve the Entity Info reports
141.371669' as the curve length (also through Text tool)
It should however be: 282.743338'16 segments out of the exploded curve add up to: 281.923143'
just a bit shorter which is obvious.
The more segments the more precise Taff's approach will be.
Even better when there were a "rotate snap" option to a curve.Regards,
Wo3Dan "*
Advertisement







