Plug-In Request: Make Model BSP Compatible.
-
I use Valve’s plug-in to bring Sketchup models into Hammer.
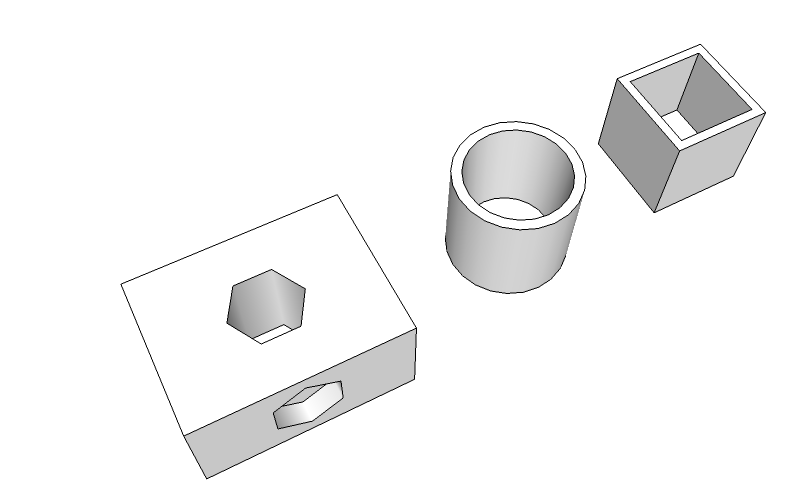
It works well but the annoying thing about it is that I have to ensure that my SketchUp models are compatible with a BSP editor. This basically means that each object I make can’t have concavity. If I make a model from scratch, I can avoid this problem by the way I construct the building, but if I receive someone else’s model, there will always be a lot of concavity, and I have to fix it all manually. It would be great if there were a way to automate this process.

Each piece is its own grouped and enclosed object.
It would be even better if it were smart enough to miter corners.

Thanks for your interest.
-
So you want each object to divide into convex hulls?
There is a tool VHACD by Khaled Mamou, and it does that pretty well.
A plugin could be written that uses VHACD to convert SketchUp geometry into convexhulls.
How the plugin could work:
The plugin will not modify geometry. Instead it will create a new layer, "Convex Decomposition", and create all convex hulls under that layer. The user could then select all that belongs to that layer, and export that selection using the Hammer Exporter. If the Hammer exporter doesn't have a feature to export from selection, then you could copy all groups from the layer, and paste them into new SketchUp instance; then use the Hammer exporter to export the whole model.I have a few questions:
- Should all generated convex hulls be top level groups or some should remain inside other groups?
- Does the SU to Hammer Exporter export textures and colors - should the newly generated convex hulls be colored?
I don't have Hammer exporter plugin, nor can I find the download link. Maybe you could send me a copy of the plugin, so I could see what and how things should be handled.
I could write a plugin that does that, but can't promise anything as it could be too complicated.
-
Hi Anton, this all sounds great, thanks for your fast response.
@unknownuser said:
Should all generated convex hulls be top level groups or some should remain inside other groups?
Yes, I would need the hierarchy of groups to remain in tact.
@unknownuser said:
Does the SU to Hammer Exporter export textures and colors - should the newly generated convex hulls be colored?
If possible I would like the hulls to retain whatever materials they had originally.
Here is a link to the Valve Plugin:
Thanks again, I'm looking forward to hearing what you come up with.
-Matt
-
I implemented V-HACD 2.2 by Khaled Mamou, but don't find results as accurate as expected. The following image was generated with resolution of 100,000 - not accurate.
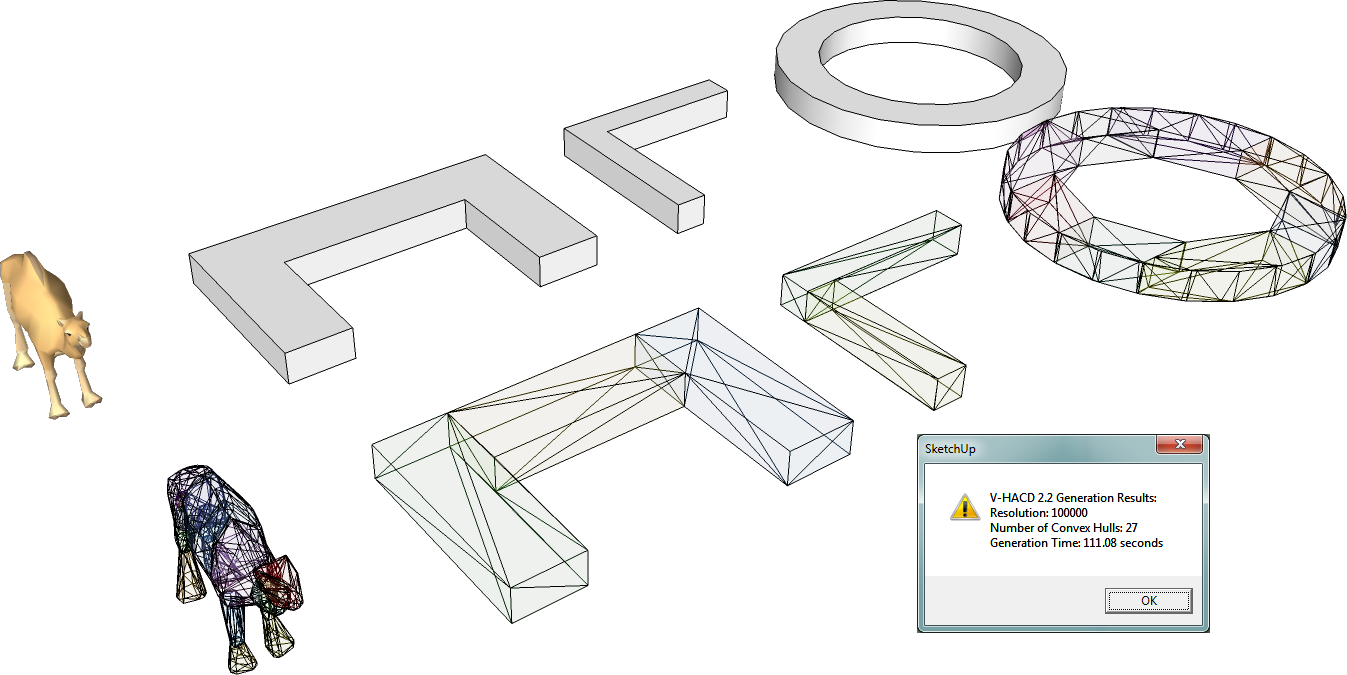

Of course, generation resolution could be increased to 10,000,000 for better accuracy, but it will take a long time to generate an accurate convex approximation.
Once someone figures out a fast algorithm to generate exact convex approximation, I will implement it, but for now, this plugin might remain as a concept.
Here is the download link if you want to try it out:
ams_VHACD_1.0.0.zipAccess
- (Menu) Plugins → VHACD → Generate Convex Hulls from Model
- (Menu) Plugins → VHACD → Generate Convex Hulls from Selection
- (Menu) Plugins → VHACD → Select Generated Convex Hulls
- (Menu) Plugins → VHACD → Erase Generated Convex Hulls
- (Menu) Plugins → VHACD → Options <- Use this option to preset generation resolution.
- (Menu) Plugins → VHACD → About
- (Edit Context Menu) → Generate VHACD Convex Hulls
-
Hi Anton,
Thanks for your work, this could really go somewhere. Unfortunately I am having the accuracy problem as you mentioned. Even on max accuracy the new model is always a little bit larger -- which makes this unworkable for my application. Also, when I use the plugin it appears to shrink-wrap the whole form as one hull rather than breaking it into several hulls. Do you have any other suggestions of what might fix these problems?
Thanks again.
- Matt
-
Some objects are wrapped because convex resolution parameter is too small. You can increase it to 10,000,000 for more consideration, but it will be too slow. Use this menu option to set resolution: (Menu) Plugins → VHACD → Options
Edit: However, it is still very likely for it to fail to generate proper convex approximation. Currently, I don't have any other suggestions to fix that.
-
Hi, I have tried it with the 10,000,000 but I'm still getting the same result.
-
Well, there is nothing I can recommend then. I'm currently developing an algorithm that will make exact convex decomposition, but again can't promise anything.
-
@anton_s said:
I implemented V-HACD 2.2 by Khaled Mamou, but don't find results as accurate as expected. The following image was generated with resolution of 100,000 - not accurate.
 So glad I saw this thread - I wanted to see this tool in action within SketchUp!
So glad I saw this thread - I wanted to see this tool in action within SketchUp! -
Interesting thread, but I don't quite catch the rationale.
Is this about cutting a solid into true convex solid, so a kind of spatial triangulation, which means that you have to figure out how to join faces to other faces?
I think it is possible to geometrically split the given geometry into blocks, but each individual block needs then to be closed to become a true solid.
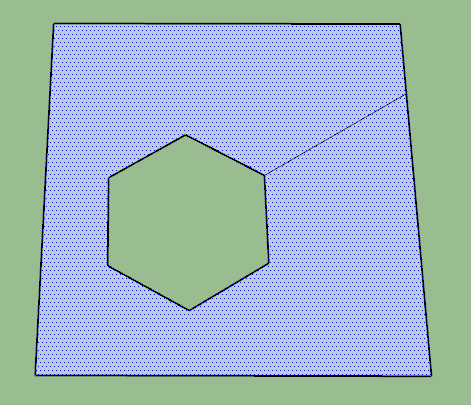
For instance, on the picture below, the faces of the initial solid are split among 4 blocks. But each block is not a solid. That would require new geometry to make them solid.
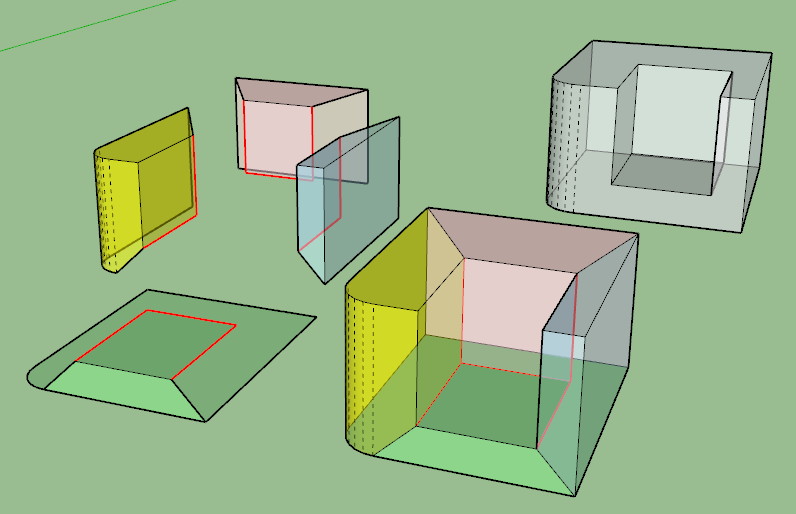
Alternatively, one can think of spliiting the solid into base tetrahedrons, and then see if some terathedrons can be merged to still garantee convexity. But the result can be ugly (as any triangulation), because a natural decomposition may be nicer by creating new vertices on edges than to only rely on original vertices.
or maybe I missed something!!
Fredo
-
@thomothom
Yep! It was quite interesting for me to see this thing up an running too.@fredo
Yes, this is about taking any solid and dividing it into convex groups. By saying dividing, I also mean adding faces at split locations to close the groups.There is one thing that I think is required for convex decomposition process. It is required to divide each face into triangles. This can be easily done via SU
Sketchup::Face.#meshfunction, which returns a triangular mesh of the face.mesh.pointsandmesh.polygonsfrom all faces is all the data the user will need to calculate the convex decomposition.Then, having everything as triangles, one can develop an algorithm that splits this triangles into covex shapes. I already developed a 2D algorithm, but 3D one seems a quite more complex.
I will post a 2D exact convex decomposition plug once I get home.
-
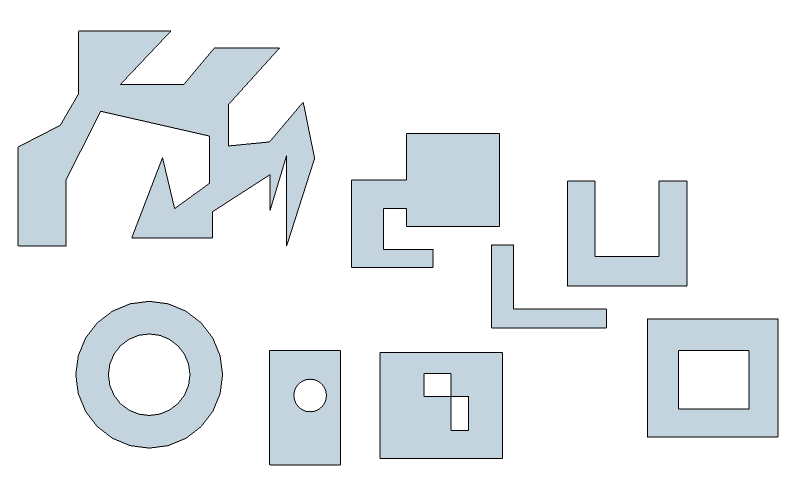
@Anton_S
Unfortunately, the Face.mesh method does not good visually nice result. I guess it is fast, but the result can be 'ugly'. I have on my roadmap to find a way to generate a nicer triangulation of faces. From there, it is relatively easy to split a face into convex portions, as below: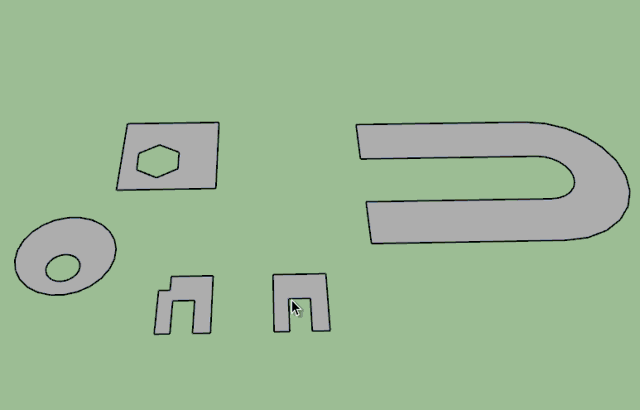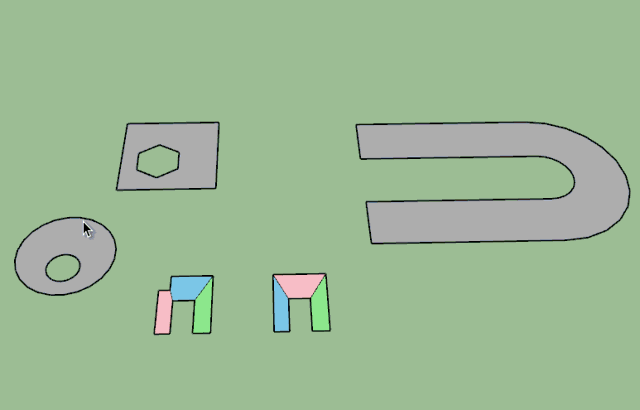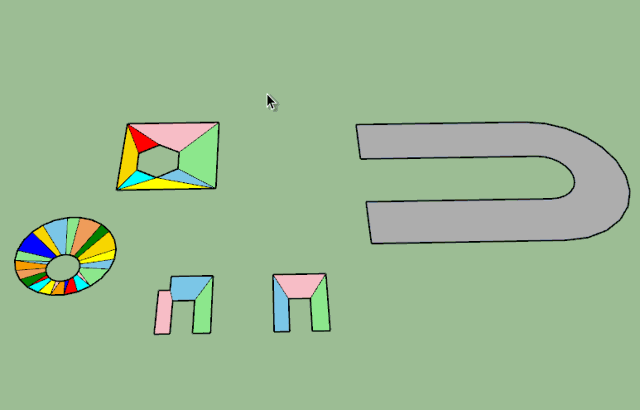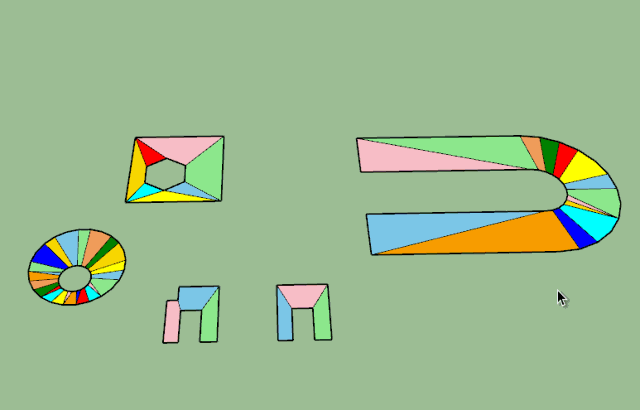
@ziiar
For the original problem of this thread, I have found a brute-force algorithm that does the job of cutting a solid into convex solids. The result may not be nice visually, even with some heuristics. Anyway, there is NO unique solution most of the time.Here is a short video to illustrate
Fredo
-
Yes, face.mesh doesn't make a good mesh, but it does the job.
Here is my 2D algorithm demonstration:
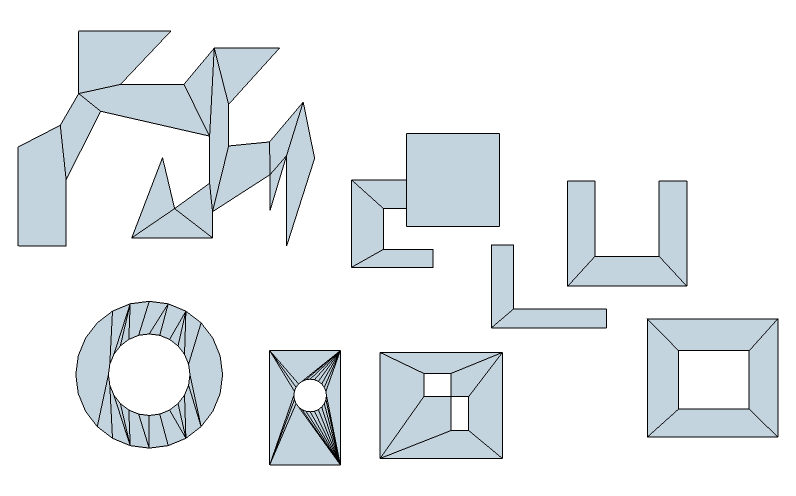
Place in Plugins folder...Your 3D convex hull decomposition is awesome! Unique results isn't a problem at all. What matters is that it works and I assume it generates very fast!

Once it is fully developed, you can share it to various physics engines, like Newton and Bullet, and they will implement it into their engine. I bet they are looking for an algorithm like that. All one will have to do is convert it to C++. And of course with your permission it could be added to my MSPhysics project, a free physics simulation that uses Newton Dynamics Physics SDK by Juleo Jerez.
-
Fredo, it would be nice to see how your 3D convex decomposition performs on these shapes:
convex decomposition.skp
Thanks -
Anton,
The algorithm works on your models. They were extremely useful because they helped me to detect a very nasty problem which I had to fight against for a few hours.

Actually the principle of the algorithm is quite simple (but the implementation is less straightforward)
Step 0: Split the selection into connected solids. This form the initial working list of solids
For each solid in the list
Step 1: Determine the concave edges (if none, then the solid is convex and go to next solid)
Step 2: Select one concave edge and take a cut plane (normally its bissector plane)
Step 3: Split the solid along this cut plane, giving 2 or more subsolids
Step 4: Put the sub-solids into the list of solids to treat
end
The heuristic is mainly about the selection of the concave edge for each solid and the best cut plane. For instance:
a) you would take first concave edges connected to other concave edges, and use the plane of these concave edges
b) then, if you find a guiding edge connected to the concave edge whose bissector plane is not too far from the bissector plane of the concave edge, then use this edge as a guide
c) for concave edges with an open angle (say > 140 degrees), the best is to take its bissector plane.
Here is an illustration of heuristic b). Obviously, with a proper triangulation and convexification of faces, these guiding edges can be computed automatically. I have done some work on it, but the 'nice' triangulation does not always work due to limitations of my algorithm (I used Delaunay triangulation and I have to implement a 'constrained' Delaunay triangulation)

I don't know too much why this convex decomposition is important in Physics engines. Are there limitation with some concave solids?
By the way, the nasty issue I was mentioning deals with copying faces when you have special cases like the one below:
The other difficulty of the algorithm is to intersect the solid and assign properly the faces which are located along the plane to the right side (this is where your models helped).
Fredo
-
These are some nice results!
I'm more of a visual person, and I don't quite understand these steps, especially step0. An animation would make things more clear for me, but it seems like it is a recursive concept; repeatedly dividing solids at special locations until they are convex.
In physics engines there is a simple way to calculate whether two convex solids intersect, i.e detect collision. When it comes to concave solids, things get more complex. Concave solids can only be static (tree or scene) collisions or be divided into convex solids and be a dynamic collision formed as compound - an array of convex solids glued together. Developers usually divide their solids into various convex shapes (manually or using VHACD) and then form them as compounds. Your algorithm would be very useful to divide solids into convex hulls automatically, just like VHACD, but with complete accuracy and good results.
I'm glad the models helped you improve your algorithm. I'll be glad to test it in various other cases once you release it.
Also, does it work with non-solids? And it does matter which side the face normal is point at, right?
-
Anton,
Here is a short animation to illustrate the algorithm.

Also, I understand now the relation with Physics engines. The algorithm uses #intersect_with, so it has to create some geometry. However, it is easy to
- create the convex solids on a specific layer, so that you can easily associate each original solid to its convex decomposition
- Transform the convex decomposition in whatever data form suitable to the physics engine to manage collisions and delete the convex solids.
The algorithm should work on 'pseudo-solids' that is solids where all edges are bordered with 1 or 2 faces (but not more than 2)
The orientation of normals is important to detect concavity of edges. Here too, it is possible to give some flexibility based on solid topology.
Fredo
-
Very nice animation, Fredo!
For ziiars purpose, creating geometry is what he needs, but when implementing this to my physics engine, I would avoid creating any geometry and try computing all intersections in a function.
` # Get all convex hulls from mesh.@param [Sketchup::Group] group
@return [Array<ArrayGeom::Point3d>] An array of convex hulls.
Each convex hull represents an array of points.
def get_convex_hulls(group)
#...
end`Then, each of these convex hulls (an array of points) could be passed to a function in physics SDK to create convex collisions from them, as Newton Dynamics Physics SDK only asks for an array of points to create a convex hull.
Although, I'm not asking you to make it the way I requested. What I'll need is the peace of code that subdivides solid into convex hull. Then I could replace the intersect_with function with a custom function to avoid creating any geometry.
Good to know that it works with 'pseudo solids'. Will be useful.
Also, you could add 'max concavity angle' parameter to your algorithm to avoid sub-diving if angle between concave edges is greater than the 'max concavity angle'. I.E control generated 'resolution'.
-
Anton,
I am afraid my implemnetation is fully based on Sketchup, not just for intersection, but for the topological relationships between edges, faces, etc....
I can adapt an API that can deliver the output as a hierachical matrix of points for groups and faces, leaving the model intact (either doing an abort_operation, or deleting all intermediary groups created).But, if you plan to build it in C++, the best is to write a native version from the algorithm. As I said, it is fairly simple, and since you do not care with the esthetics of the decomposition, it can even be simpler. I can send you the details of algorithm, so that based on your C++ environment to describe the toplogy, you see how to adapt it to integrate with the Physics engine.
Fredo
-
By the way, the algorithm happens to work on 'open solids', that is solids where edges are connected to 2 or 1 faces.
However, I am not sure the result is useful, as it gives potentially open solids too.

Fredo
Advertisement








