3D Truss Models

medeek

Enabled mod warren webs for the double pitched flat truss configuration:

The truss shown above is an asymmetric double pitched top chord bearing flat truss with a mod warren web configuration and cantilever ends. That is quite a mouthful.

I have not added the top chord bearing option and the mod warren webs to the other flat truss configurations yet (flat, monopitch, pitched), however I will if specifically requested.

As Facer has duly noted priorities are critical and there a much hotter items on the plate.

The stepdown hip truss set is the big one, that is next, and yes it will be a game changer.

The flat truss was just a primer to warm up my programming chops, its been almost a month since I was able to touch the truss plugin.

medeek

Since about version 1.6.0 I've been tracking every installation of the plugin. The funny thing is that I see more installations of previous versions of the plugin than I do of the current version. I am wondering why that is and also where the previous version is being distributed from. It's not a huge deal but it does have me wondering.

juju

That is a sign of a software being worthwhile, it gets pirated (unfortunately). Maybe chat to some of the other devs (ThomThom / Whaat / etc.) about how they go about curbing this scourge.

medeek

I don't know that its a sign of hacking as much as people not having access to the most recent version of the plugin. Possibly two reasons:

1.) The user downloads a version of the plugin and then installs it months later.
2.) Other websites are redistributing the plugin (older versions).

I don't provide links to previous versions on my website since the latest version is always better than the last, so again this doesn't make much sense to me.

medeek

In the global settings I've added a setting to switch between metal and wood connector plates. Initially I will only enable wood plates for some of the more typical common trusses (ie. fink, howe, queen and king), if this feature proves to be popular I may enable it for more truss types.

medeek

Version 1.9.1 - 06.09.2017

Added plywood gusset plates for common fink trusses.
Enabled a "WOOD" plate type option in the global settings.

*Note that the wood gussets are currently only available for the Fink truss, if anyone needs them enabled for a different truss please let me know.

View model here:

https://3dwarehouse.sketchup.com/model/f6e1ea1b-f485-41b3-9d11-cd6d2c71087c/Wood-Gusset-Connected-Trusses

medeek

Added plywood gusset plates for raised heel common fink trusses.

View model here:

https://3dwarehouse.sketchup.com/model/b21431bc-c3b6-4038-a81e-f27fc78f69b1/WGC-Truss

Note that there are currently no calcs associated with these WGC trusses. If you are going to build your own trusses I would strongly suggest you find a local structural engineer to assist in specifying the plates sizes and fasteners, especially if the truss span is greater than 16 feet and your snow loads are greater than 25 psf in your region.

When I engineer WGC trusses I will also call out a waterproof glue as well however I don't take the glue's strength into the calculations. This provides another margin of safety and also the rigidity of a glued and nailed gusset plated truss is superior in my opinion to your typical MPC truss.

Every member is critical in a truss, however some are more stressed than others. Your top and bottom chords should never be anything less than a No. 2 DF. I would suggest No. 1, No. 1 & Btr. or Select Structural. The webs of a typical truss are usually stressed quite a bit less than the chords and sometimes you can get away with stud grade lumber but I would suggest DF No. 2 on all webs as well. A strategically placed knot can easily ruin an entire truss.

Just as important as the materials is the level of care taken in cutting the members and assembling the truss. All joints should fit tightly together so that members in compression can bear directly on their adjacent members. Also realize that tension members may experience load reversals in high wind or seismic events so even tension members are no exception to the rule.

The correct fasteners and fastener size is critical. The nails will be in single or double shear and the joint connection is relying entirely on this shear strength of the fasteners to hold together. Fasteners too close to the edge or ends of a member are not as effective, so fastener placement is also critical.

I am curious how the two truss types would compare in a burn test, which one would stay intact longer. My suspicion is that the plywood gussets would char and slowly burn however the metal plates would heat up and loose their strength quickly and fail.

I know most people don't do this but I would personally stress test each truss before installing it on the intended structure. Mostly what you are looking for is a uniform deflection across all the trusses so that they can load balance properly. If a truss is defective this test should help ferret out this data even though visually the truss may look acceptable.

medeek

Just for the record the algorithm to size and position the mid top chord to web plate (Plate 2) is a real piece of work:

gamma2 = 3.14159265358979 * 0.5 - @Phi
length2 = @Pldim2 * 0.5 -1
p3x = @Swx4 + length2 * (cos(@Theta2) / cos(gamma2 - @Theta2))
p3y = @Swy4 - length2 * (sin(@Theta2) / cos(gamma2 - @Theta2))
p2x = p3x - (@Tcd + length2) * cos(gamma2)
p2y = p3y + (@Tcd + length2) * sin(gamma2)
p1x = p2x - @Pldim2 * cos(@Phi)
p1y = p2y - @Pldim2 * sin(@Phi)
length4 = sqrt((@Strx4 - p1x)*(@Strx4 - p1x) + (@Stry4 - p1y)*(@Stry4 - p1y))
zeta2 = atan((p1y - @Stry4)/(@Strx4 - p1x))
length3 = length4 * sin(zeta2 + @Theta3) / sin(3.14159265358979 * 0.5 + @Phi - @Theta3)
p4x = p1x + length3 * cos(gamma2)
p4y = p1y - length3 * sin(gamma2)

if @Theta2 > gamma2
  p2x = p3x - ((@Tcd + length2) / (cos(@Theta2 - gamma2))) * cos(@Theta2)
  p2y = p3y + ((@Tcd + length2) / (cos(@Theta2 - gamma2))) * sin(@Theta2)
end

Actually had to use the Sine Law: https://en.wikipedia.org/wiki/Law_of_sines

Its funny because my 15 year old daughter just covered trigonometry in her math class and she told me she would never use this stuff so why learn it.

pbacot

Nice additions to the plugin. Impressive work too. I guess you have engineering training but what else has helped you tackle these programming problems?

Peter

medeek

There is really very little engineering going on in this plugin, at least for now. Most of it is boolean algebra (conditional statements and a few loops) and a lot of geometry most of which can be solved with simple trigonometry. In a few cases I have to implement an iterative solution so convergence is sometimes an issue. The rest of it is simply manipulating the SketchUp API so that it produces the correct output, that is my Achilles heel.

medeek

I may have opened Pandora's box with the addition of the WGC fink trusses. I've now had a couple of requests for cut list associated with these trusses. I don't think it would be that hard to generate an html output using SVG showing the various members and their dimensions. This can then be printed to a PDF document by the user.

Any thoughts on creating construction drawings this way. I am essentially bypassing SketchUp's Layout with an Html/SVG solution but perhaps there is a better way.

juju

If you're going that route be 100% sure the engineering is correct.

Personally, I think that is going tò far for general use, but may be fine for an engineering version.

medeek

It's definitely not on top of the todo list but it is interesting how quickly there was a response and request for a cut list of construction drawings.

I agree if I'm to take it this far I will probably want to make sure the engineering is bullet proof, so the short answer for now is that it is probably not going to happen in the near future.

medeek

I've had a request for an option that makes it so the plugin only draws the top and bottom chords and not the webs. I guess I could see a reason for this in some situations. I'm just wondering if there are any others who would be interested in this option.

medeek

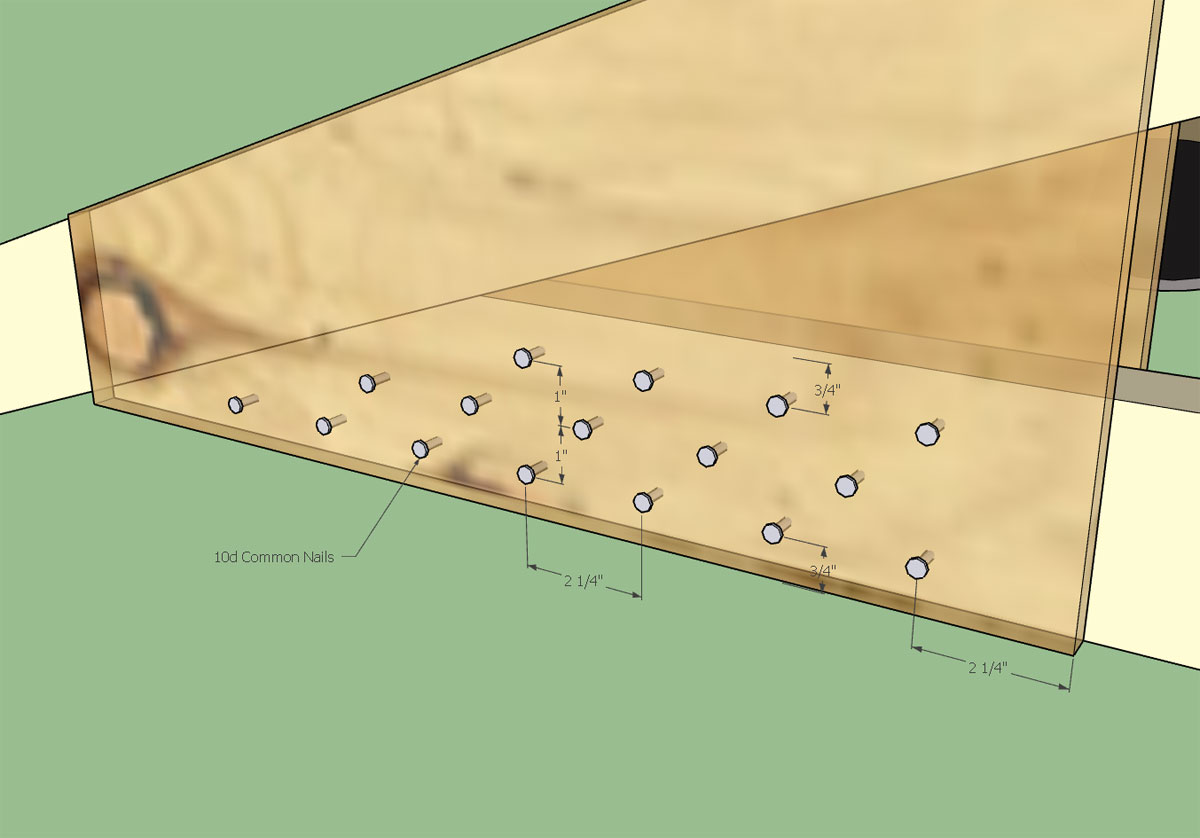
I've been thinking about site built trusses some more and trying to apply some rational thought to how best to nail together a WGC truss. If you consider nails in single shear, 8d nails spaced at 4" between fasteners with a row spacing of 1" and and end spacing of 1.5" you end up with something like this.

Those are 8d common nails so they aren't very big but spaced at 2" between nails in a row I would be afraid of splitting that bottom chord.

Looking at this I'm fairly convinced that going with longer nails that are in double shear and clinched give more bang for the buck, allow less nails and thereby less chance of splitting the truss members. Thoughts?

medeek

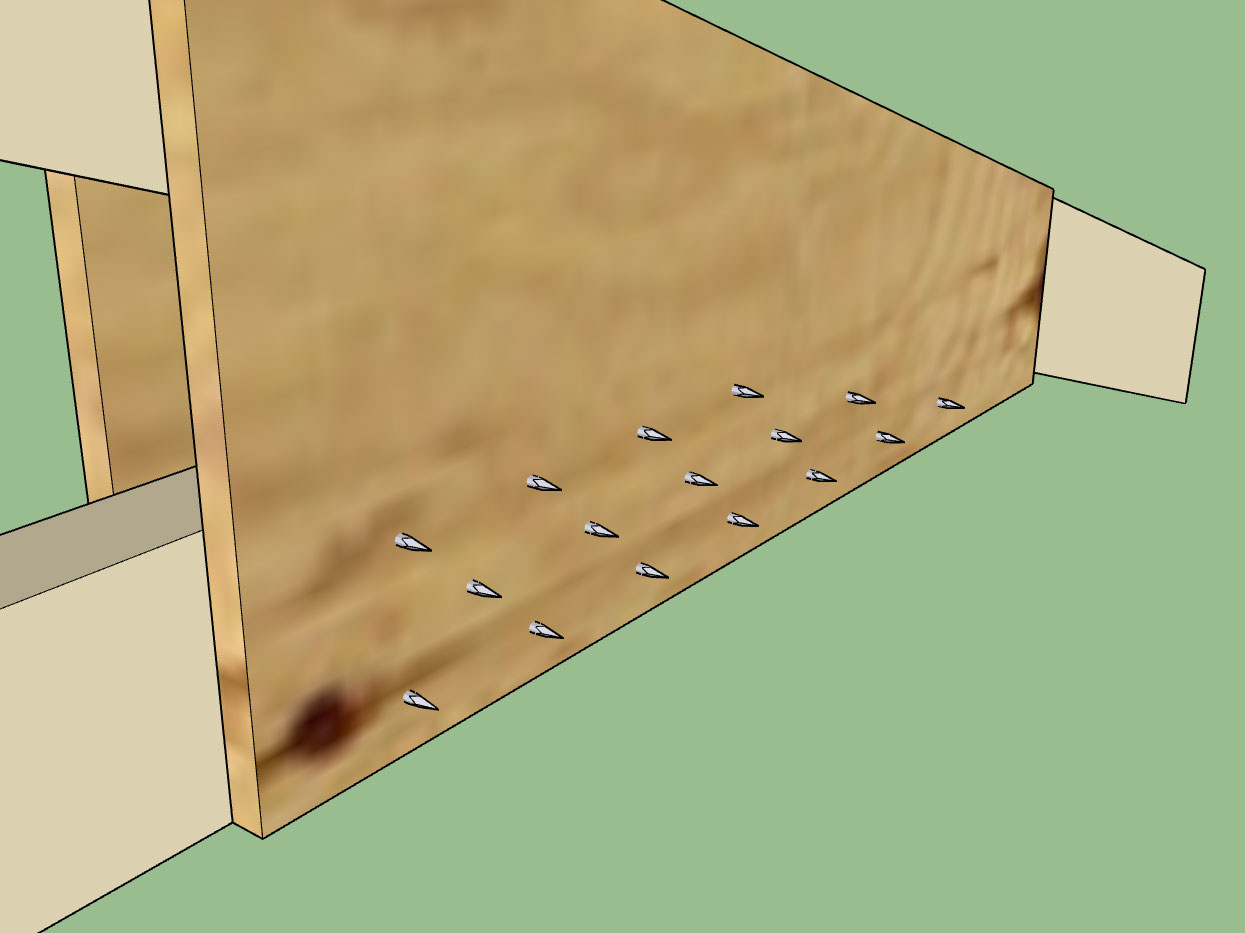
Nailing from both sides is not reasonable in my opinion, there is no way to line up the nails easily from one side to the other, better to just nail from one side which bring me back to nails in double shear.

Using a 10d common nail (.148 x 3) and with 1/2" of protruding nail to clinch I get this layout:

with the backside looking something like this:

I probably don't need a 2.25" end distance (15D) on the plate edge toward the inside of the truss but I am using Table C11.1.6.6 from the NDS Commentary (NDS 2012).

medeek

If you compare the capacity of a single shear and double shear connection in most cases you get double the capacity, see results for a 10D nail into DF and Structural 1 Plywood below:

So returning to our previous example we now have 2180.9lbs/176.3lbs = 12.4 => 13 fasteners in double shear, rather than 25 fasteners in single shear, a much more reasonable number of fasteners

medeek

If we consider the peak joint as rigid (web joints are pin jointed), one can see that the moment at the peak is fairly substantial (145 ft-lbs):

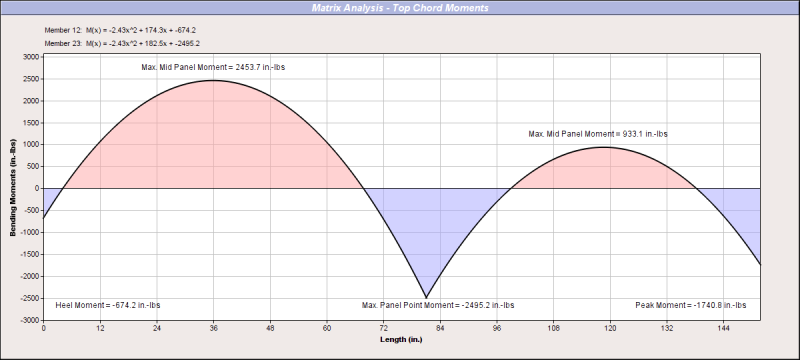
Both the top chords are in compression and pushing against each other, so the member on member contact is transferring a significant amount of that compressive axial load.

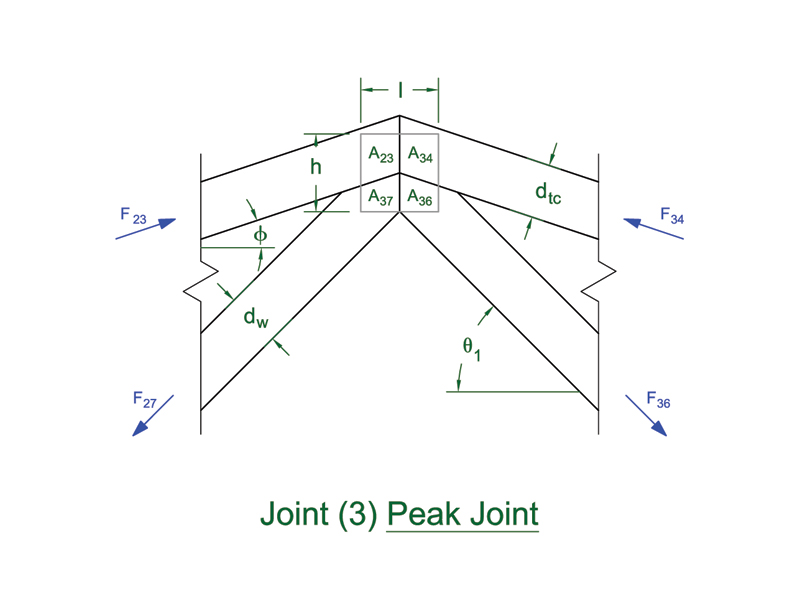
To account for the component of the load that is not being transferred at this joint I can probably use the equation from the TPI 1 for MPC trusses:

Pc' = sqrt(P[sub:y7ifrpex]P[/sub:y7ifrpex][sup:y7ifrpex]2[/sup:y7ifrpex] + (P[sub:y7ifrpex]N[/sub:y7ifrpex] x C[sub:y7ifrpex]r[/sub:y7ifrpex])[sup:y7ifrpex]2[/sup:y7ifrpex] (Sec. 8.3.3.3)

where:

P[sub:y7ifrpex]c[/sub:y7ifrpex]' = Resultant compressive force used for determination of minimum required metal plate contact area (lbs)
C[sub:y7ifrpex]R[/sub:y7ifrpex] = Reduction factor for cmopression force component across the joint interface for metal connector plate design: 0≤CR≤1.0 (lbs)
P[sub:y7ifrpex]iN[/sub:y7ifrpex] = Compression force component of the wood member under investigation normal to the wood member interface (lbs)
P[sub:y7ifrpex]iP[/sub:y7ifrpex] = Compression force component of the wood member under investigation parallel to the wood member interface (lbs)

With the resultant being:

CR = 0.5
Pi = F23 = 2021.83 lbs.
PiN = Picos(Φ) = 2021.8 x cos(18.43) = 1918.1 lbs.
PiP = Pisin(Φ) = 2021.8 x sin(18.43) = 639.4 lbs.

θ = atan(PiP/PiN x CR) - Φ = atan(639.4/1918.1 x 0.5) - 18.43 = 15.3 deg. (angle between resultant compressive force and chord member)

Pc' = √(PiP)2 + (PiN x CR)2 = √(639.4)2 + (1918.1 x 0.5)2 = 1152.6 lbs. @ 15.3 deg.

I kind of get the logic behind this equation but I question where does the Cr (reduction factor) come from? and why a value of 0.5?

I'm also looking at the rather large moment at this joint between the two top chords and wondering how best to factor that in.

medeek

To allow for these same moment effects at the heel of a truss the TPI stipulates a heel reduction factor H[sub:2y81ofvw]R[/sub:2y81ofvw] = 0.85 - 0.05(12tanθ -2.0) Sec. 8.3.2.2. I'm going to assume this is an empirical formula developed over years of testing and experience. However, for all non-heel joints this reduction factor is 1.0, which makes sense for an MPC truss but maybe not for a WGC truss, where moments at the joints are going to be larger due to the rigidity of the connection.

In the TPI 1-2014 commentary there is some good discussion on combined axial and moment loading scenarios. Equation E C8.7-1 approaches this problem by converting the moment into an equivalent tension force: Teq = 6M/d.

The logic behind this is to start with the bending stress and multiply it with the cross sectional area of the plates: (1) T[sub:2y81ofvw]eq[/sub:2y81ofvw] = f[sub:2y81ofvw]b[/sub:2y81ofvw] x 2dt

Where: f[sub:2y81ofvw]b[/sub:2y81ofvw] = M/s and S = 2(td[sup:2y81ofvw]2[/sup:2y81ofvw]/6)

Substituting into equation (1) yields the 6M/d expression.

The commentary notes that this method has proven to be conservative (which I like) in most situations however they have since supplanted it with a more complicated and accurate approach.

For analysis of the tensile capacity of the actual gusset plates (plywood or OSB), tension check, this addition of an equivalent tensile force seems to make sense to me.

T[sub:2y81ofvw]tot[/sub:2y81ofvw] = T[sub:2y81ofvw]axial[/sub:2y81ofvw] + T[sub:2y81ofvw]eq[/sub:2y81ofvw]

This is essentially the same as equation 3.9-1 in the NDS and can be written in this form:

The applied stress would then be: T/2td + 6M/2td[sup:2y81ofvw]2[/sup:2y81ofvw] which must be less than Ft' the allowable tensile stress of the plywood.

With the analysis of the fasteners (nails) one could probably use a simplified approach like this or a more complicated nail group analysis like I've used in calculating portal frames.

medeek

With the nail group calculation knowing the number of required nails, row spacing, nail spacing in a row one can come up with a rectangular approximation of the area filled with this group of nails.

The force applied to the worst case nail would:

F[sub:10dybyec]nail[/sub:10dybyec] = M[sub:10dybyec]joint[/sub:10dybyec]S[sub:10dybyec]x[/sub:10dybyec]S[sub:10dybyec]y[/sub:10dybyec]r[sub:10dybyec]max[/sub:10dybyec]/J

Where the Polar Moment of the Nail Group is given by J = bh[sup:10dybyec]3[/sup:10dybyec]/12 + b[sup:10dybyec]3[/sup:10dybyec]h/12: b = r[sub:10dybyec]x[/sub:10dybyec] + s[sub:10dybyec]x[/sub:10dybyec], h = r[sub:10dybyec]y[/sub:10dybyec] + s[sub:10dybyec]y[/sub:10dybyec]

and

s[sub:10dybyec]x[/sub:10dybyec] = nail spacing in x-dir
s[sub:10dybyec]y[/sub:10dybyec] = nail spacing in y-dir
r[sub:10dybyec]max[/sub:10dybyec] = distance from centroid of rectangle to corner (furthest fastener)

This won't be entirely accurate since the fasteners will probably not form a perfect rectangle but it should be reasonably close.

Then one can add this worst case nail force to the average force on the nails from an axial member load (conservative) and come up with the combined load on the worst case fastener.

This becomes an iterative process:

Step 1: Compute the number of fasteners for only the tensile load.
Step 2: Given the number of fasteners and fastener group geometry from Step 1 then calculate the load on the worst case fastener in the group.
Step 3: Add the value in Step 2 to average value from Step 1 and check against the allowable for the fastener. If it exceeds the allowable then add a fastener and repeat the computation of the average fastener load due to tensile load only and the load due to the moments, repeat until it passes.

It's no wonder that the truss companies have all of this stuff programmed. Technically this needs to be done for each joint at each load case, since load reversals may turn a compression loaded joint into a tension joint and vice versa, and the moments will be different for each load case.

As you can see engineering a truss (WGC or MPC) is no trivial matter.