Negative uniform scale

Roschetch

Select a component or group and try this:

selected = Sketchup.active_model.selection[0]
selected.transform! Geom;;Transformation.scaling(-1)

Where is your group?
If you open the Outliner window, you will see that the group is there and may be open for edit.

If you check the group transformation, you will get:

selected.transformation = Geom;;Transformation.scaling(-1)
selected.transformation.to_a
[1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, -1.0]

To make your group reappear, do:

selected.transform! Geom;;Transformation.scaling(-1)
selected.transformation.to_a
[1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0]

And after that try:

selected.transform! Geom;;Transformation.scaling(-1,-1,-1)
selected.transformation.to_a
[-1.0, 0.0, 0.0, 0.0, 0.0, -1.0, 0.0, 0.0, 0.0, 0.0, -1.0, 0.0, 0.0, 0.0, 0.0, 1.0]

According to the API, there would be no difference between
Geom::Transformation.scaling(a,a,a) and
Geom::Transformation.scaling(a)
But this is not true for negative scales.

There is not essentially wrong with a non unitary last element in the transformation matrix. For instance:

selected.transform! Geom;;Transformation.scaling(2)
selected.transformation.to_a
[-1.0, 0.0, 0.0, 0.0, 0.0, -1.0, 0.0, 0.0, 0.0, 0.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.5]

works great.

Is this a bug? Is it restricted to SU 8?

tt_su

@roschetch said:

According to the API, there would be no difference between
Geom::Transformation.scaling(a,a,a) and
Geom::Transformation.scaling(a)
But this is not true for negative scales.

Haven't dug into this - but I do recall that Geom::Transformation.scaling(a) and Geom::Transformation.scaling(a,a,a) have (at least in the past) done different things to the transformation. I think the latter yielded a transformation where several render engines didn't recognise the scaling properly.

TIG

If you don't mind your brain hurting a bit...
Do a thought experiment...

Remember that scaling and rotation are inexorably linked...
The order of the scaling steps affects the result...
Some scalings cancel earlier ones...

Scale something -1,1,1 about its center and if flips along its x-axis - it is a mirrored version [aka handed].

There are now three possible handing scaling operations...
2a. You scale it -1,1,1 and it reverts to the unhanded form - as if you had done no steps at all.
2b. Alternatively scale it 1,-1,1 and it now flips along its y-axis:
it is no longer handed [it is its original handing] but it is oriented as if the original had been rotated about the z-axis by 180 degrees.
2c. Alternatively scale it 1,1,-1 and it flips along its z-axis:
it is still handed and it is now oriented as if you had rotated the step 1 result about the x-axis by 180 degrees.

Now scale it again 1,1,-1...
3a. Applied to the result from step 2a the form is re-handed, and as if you had rotated the result in step 1 about the y-axis by 180 degrees.
3b. Applied to the result from step 2b the form is re-handed, and as if you had rotated the result in step 1 about the x-axis by 180 degrees.
3c. Applied to the result from step 2c the form is re-handed, but it is as if you had stopped at step 1

Obviously you can do these steps in different orders, but it should become clear that they will sometimes undo a previous handing and are then equivalent to a rotation, depending on the order of the scaling steps.

So to recap: scaling in three steps by -1, just in x, then just y, then just z [steps 1/2b/3b], is the equivalent result to just scaling -1 about the x-axis in one step [step 1] [the subsequent second and third scalings for y and z effectively cancel out each others 'handing' ?]!

Since a combined transformation of -1,-1,-1 effectively does these steps, then you could have used -1,1,1 [with a rotation] instead and got the same result ?

Roschetch

@tig said:

So to recap: scaling in three steps by -1, just in x, then just y, then just z [steps 1/2b/3b], is the equivalent result to just scaling -1 about the x-axis in one step [step 1] [the subsequent second and third scalings for y and z effectively cancel out each others 'handing' ?]!

Since a combined transformation of -1,-1,-1 effectively does these steps, then you could have used -1,1,1 [with a rotation] instead and got the same result ?

I do not understand your conclusion. Your drawings/examples seem to contradict it. The scaling by (-1,-1,-1) (steps 1/2a/3b) is handed but different from the scaling of step 1. Scaling (-1,-1,-1) is an uniform scaling but (-1,1,1) is not.

In 3D coordinate system, scaling may be represented by a 3x3 diagonal matrix. However, SU uses the uniform coordinate system (a 4D coordinate system) where geometrical operations are represented by a 4x4 matrix and points by 4 coordinates. The main purpose of this system is to unify parallel and perspective projections or, more properly, unify affine and projective transformations. Except by the 4x4 transformation matrices, we cannot access the forth coordinate of points in SU but it is there inside the code. When we code point.to_a, SU divides the first 3 coordinates of point by the fourth coordinate before presenting them. This is a projection from 4D in 3D.

"Usually" the 4th coordinate of points equals to one. But, if it is something else (except zero!), all first 3 coordinates will be divided by something different from one in the 3D projections. So, to produce a uniform scaling of points we can either change the first 3 coordinates or just change its 4th coordinate. When we create a scaling with Geom::Transformation.scaling and just one argument, SU adopts the later method, that is, change just the 4th coordinate. You can see it by printing the transformation matrix.

I think that the incorrect presentation of groups and components transformed by negative uniform scaling is not a bug in the transformations themselves but in the way SU handle the viewing of points with a negative values in their 4th component. I could not observe any positive uniform scaling bug.

fredo6

The two forms of the transformation matrix are equivalent. So there should be no difference when you apply the transformations to an object. Nothing to do with SU.

Fredo

Roschetch

@unknownuser said:

The two forms of the transformation matrix are equivalent. So there should be no difference when you apply the transformations to an object. Nothing to do with SU.

Do you mean that Geom::Transformation.scaling(-1) and Geom::Transformation.scaling(-1,-1,-1)
are equivalent? I agree they should. I applied them to non grouped entities and got the expected results. But try applying them to a group or component instance. You will get surprisingly different results at least in SU 8.

tt_su

Just to illustrate how Geom::Transformation.scaling(2) and Geom::Transformation.scaling(2, 2, 2) yield a different matrix in SketchUp: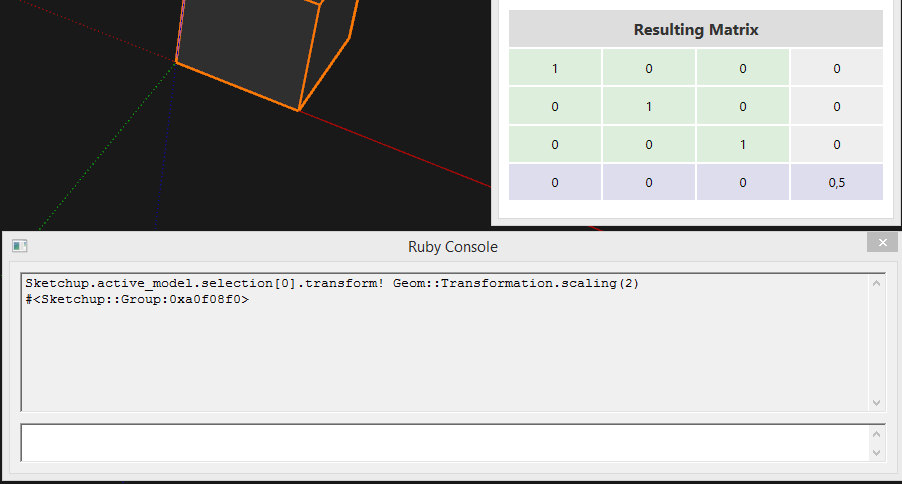

Geom::Transformation.scaling(2)

Geom::Transformation.scaling(2, 2, 2)

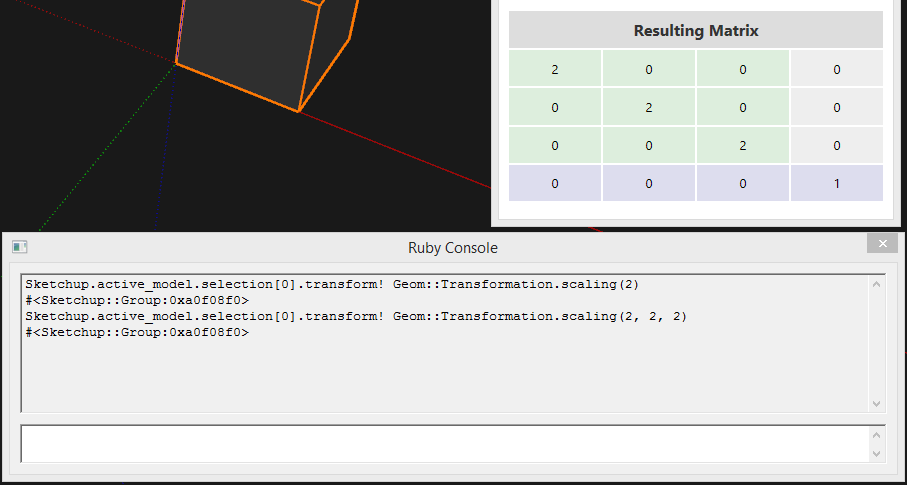
In this case SketchUp do treat them both visually the same.

But when I use negative scaling:

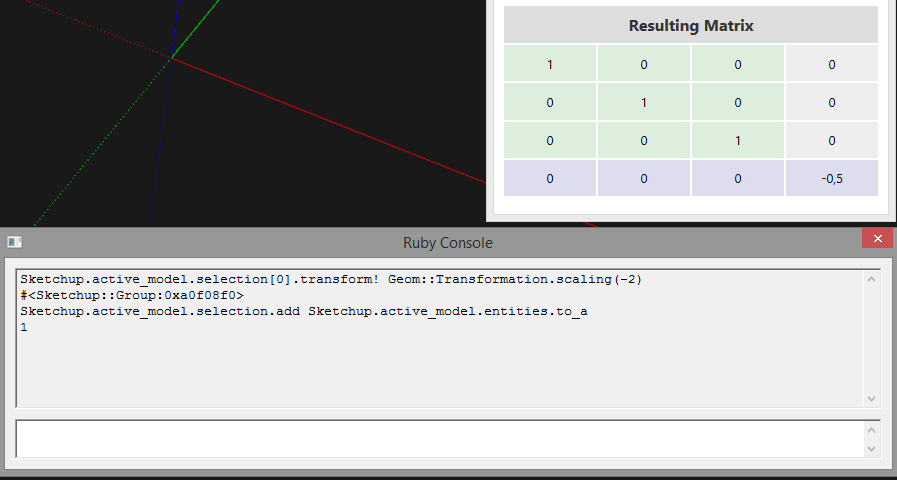
Geom::Transformation.scaling(-2)

Geom::Transformation.scaling(-2, -2, -2)

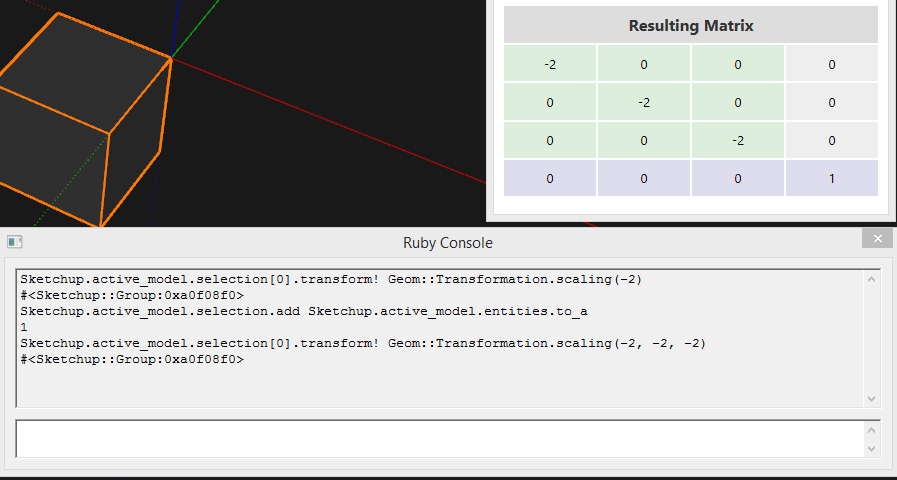
That disappearing group (visually) sure looks like a bug. I'll file a bug internally (SU-29499).
Meanwhile, the workaround is to specify scaling in X Y and Z explicitly.

TIG

Sorry to be late in responding...
What I was trying to explain is that doing all three scaling at -1 is the same as scaling -1,1,1 the rotating about the Y axis 180 degrees.

It is no coincidence that 1 PI radians is 180 degrees.
Scaling and rotation are linked...
Look at this...

###
trans=e.transformation.to_a

        scalex = Math.sqrt(trans[0]**2+trans[1]**2+trans[2]**2)
        scaley = Math.sqrt(trans[4]**2+trans[5]**2+trans[6]**2)
        scalez = Math.sqrt(trans[8]**2+trans[9]**2+trans[10]**2)
                 
        scale = scalex
        scale = scaley if scaley>scale
        scale = scalez if scalez>scale

        puts "         <pos>#{trans[12]} #{trans[13]} #{trans[14]}</pos>\n"
        puts "         <scale>#{scale}</scale>\n"   
        puts "         <rotation>\n"
        puts "            <matrix>\n"
        puts "               #{trans[0]/scalex} #{trans[4]/scaley} #{trans[8]/scalez} #{trans[1]/scalex} #{trans[5]/scaley} #{trans[9]/scalez} #{trans[2]/scalex} #{trans[6]/scaley} #{trans[10]/scalez}\n"
        puts "            </matrix>\n"
        puts "         </rotation>\n"

###
aT = e.transformation.to_a
  # aT[12], aT[13], aT[14]           x, y, z offsets from component origin
  # suATan(aT[0], aT[1])             xy plane angle
  # xy = (aT[8]**2 + aT[9]**2)**0.5
  # suATan(xy, aT[10]) - 90          rise angle, check this one
###

Roschetch

@tig said:

What I was trying to explain is that doing all three scaling at -1 is the same as scaling -1,1,1 the rotating about the Y axis 180 degrees.

Scaling and rotation are linked...

Orig = Geom;;Point3d.new(0,0,0)
Point3d(0, 0, 0)
y_axis = Geom;;Vector3d.new(0,1,0)
Vector3d(0, 1, 0)
Geom;;Transformation.scaling(-1,1,1).to_a
[-1.0, 0.0, 0.0, 0.0,  # formated manually for easy viewing
 0.0, 1.0, 0.0, 0.0,
 0.0, 0.0, 1.0, 0.0,
 0.0, 0.0, 0.0, 1.0]
Geom;;Transformation.scaling(-1,-1,-1).to_a
[-1.0, 0.0, 0.0, 0.0,
 0.0, -1.0, 0.0, 0.0,
 0.0, 0.0, -1.0, 0.0,
 0.0, 0.0, 0.0, 1.0]
Geom;;Transformation.rotation(Orig,y_axis,Math;;PI).to_a
[-1.0, 0.0, -1.22464679914735e-016, 0.0,
 0.0, 1.0, 0.0, 0.0,
 1.22464679914735e-016, 0.0, -1.0, 0.0,
 0.0, 0.0, 0.0, 1.0]

So, they are all different! But, yes, the transformations
[pre:lswzgknb]Geom::Transformation.scaling(-1,+1,-1)
Geom::Transformation.rotation(Orig,y_axis,Math::PI)[/pre:lswzgknb]are equal (within a certain precision).

Roschetch

@tt_su said:

That disappearing group (visually) sure looks like a bug. I'll file a bug internally (SU-29499).
Meanwhile, the workaround is to specify scaling in X Y and Z explicitly.

Ok, Thom. It is a small bug but it took me a long time to be assured it was not my code fault and try another way to do it.