Find plane at intersection of 2 vectors
-
I'm trying to get my head around finding a plane that is at the intersection of 2 vectors.
Think of it as calculating the angles to cut a compound miter for moulding and the plane I'm after is the plane representing the cut surface of the miter.
In sketchup I have 2 lines that intersect - I know where they intersect - but am not seeing how to derive the plane.
-
if ipoint is the intersect point ...
Would normalizing both vectors and using their sum method produce the normal vector for the miter_plane ?
miter_plane = [ ipoint, vec1.normalize.+(vec2.normalize) ]?
-
I was thinking that adding the 2 normalized vectors together should result in a vector that has a plane which is perpendicular to the resulting vector.
-
Maybe I'm going about this the wrong way. but I was hoping to use the plane to transform a moulding profile - but it would have to stretch in X and Y and rotate along the plane.
-
Another strategy is to come up with this plane - transform the moulding to the first vector and use the points in sequence and intersect_line_plane.
I'm just a bit slow at getting my head around all the necessary transforms.
Have I left you totally confused?
-
-
#Assuming you have two 'lines' [i.e. line1=edge1.line etc] that you hope intersect ?
...
pt=Geom.intersect_line_line(line1, line2) return nil unless pt vec1=line1[1] vec2=line2[1] ang=vec1.angle_between(vec2) nor=vec1.cross(vec2) tr=Geom::Transformation.rotation(pt, nor, ang/2) vec1.transform!(tr) miter_plane=[pt, vec1]
If that's not it then rotate it by(ang/2)+90.degrees? -
Thanks Tig,
That will work for strategy 2.
This strategy may accumulate errors as I walk down the path. I will check it out over the weekend. -
I checked it out and it appears that the miter_plane is always vertical and not a compound miter. What I was looking for - like on a compound miter saw is to change the angle of the miter saw so as to cut a compound miter.
What I am missing is how to rotate in 2 planes at the same time.
-
What is really interesting is that Dan Rathbun's solution produces the same plane as does Tig's, except Dan's does it with 1 line of code.
miter_plane = [ ipoint, vec1.normalize + vec2.normalize ]
-
Did you use the 'cross' to get the axis of rotation ?
-
I believe that I did
v = vec_1.clone
ang = vec_1.angle_between( vec_2 )
if ( ang != 0 )
nor = vec_1.cross( vec_2 )
tr = Geom::Transformation.rotation( pt1, nor, ang / 2.0 )
vec_1.transform!( tr )
miter_plane = [ pt1, vec_1 ]p3 = [] for pt in p2 line = [ pt, vec_1 ] p = Geom.intersect_line_plane( line, miter_plane ) p3 << p ent1.add_cpoint( p ) endend
-
I found an error where I was setting z to 0 for the vectors - I changed that and I am getting closer.
At least I can get a compound plane with Dan's code. I have several errors doing it the other way and have to test for ang != 0 and now also test for transformation.rotation as it says it can't create a vector that has 0 length.
I'll keep chunging along !
-
Ok - the premis for my strategy 2) is flawed. The code works - but produces a twist in the profile as it changes elevation.
strategy 1) is still not figured out.
The way I have been handling this is first of all transform scaling in the x direction. Then rotating and placing. It produces a result that will work but only if there is a consistent pitch if working with an elevation change. This is the second picture.
The problem here is if we start changing the pitch to close to vertical then the shape is wrong.
It appears that there has to be a compromise Conceptually if I use strategy 2 and come from both sides the intersect_line_plane will produce points that do not meet. Perhaps taking the midpoint between each pair ( 1 pt from vector 1 and the other pt from vector 2 ) it may produce an acceptable compromise. Just speculating as it is a bit difficult to visualize.
-
If you think about the real world...
It's quite possible to have two profiled cross-sectioned extruded objects [like handrails] meeting on a center-line but being rotated in the long axis.
Thus, if you cut mitered ends they will meet with a common miter-face BUT the various vertices of the profile's face will never match up.
It's just a fact of geometry...That's what joiners invented 'wreathing' to join two profiled handrail sections neatly at a major change in direction...
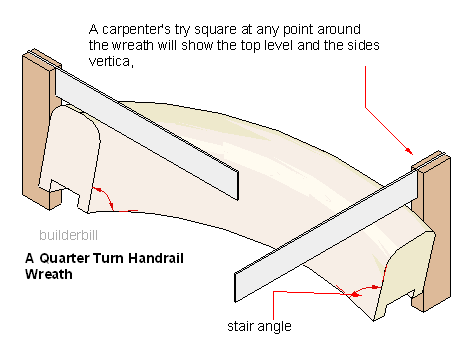

-
I know exactly what you mean - I've built a lot of curved staircases.
The challenge when it comes to modelling is to try an approximate the handrail profile and to manage ( or control ) the distortion. You feather the distortion over a distance so as to minimize it visually.
Advertisement







