Ordering 3dpoints ?

Dan Rathbun

PS: I don't think it is a good idea to extend the Array and Float ruby classes. Better used a specific private method

And I was going to say the same... and also suggest a compare method with multiple arguemnts.

1) Never extend Ruby base classes, solely to solve one coding challenge that only applies to your project. Use a custom subclass and extend that subclass.
IF you absolutely must have an instance method that acts on the object... then you should create a custom Array subclass and/or a custom Float subclass, and then add your custom methods to those custom classes.

2) Custom classes are never defined at the top level (only Ruby base classes are.) Just because someone else does it, does not mean you should.
Just as Google defined their custom classes inside the modules (Sketchup, UI, Geom,) you should define any custom classes inside your Toplevel module (but they can be nested inside submodules if you wish.)

3) There is an alternative to extending base classes or creating a custom subclass. It's called extending an object. You create a mixin module that has your custom method(s) in it, written as instance methods (not module methods.) Then when you have an INSTANCE object, you extend that specific object via:
require 'epsilon_compare.rb' my_array.extend(EpsilonCompare)
Then that specific array (and only that array,) will have your custom method(s). This way you do not interfere with the rest of the Ruby world's use of the Array class.

4) Sometimes it is necessary to extend or fix a base class for everyone, but this should be done with community approval... and likely for temporary use only, until either the SU API or the Ruby Core can be updated to include the fix or feature. (I'm actually working on such a global fix right now.. but I will post it in the SKX forum for comment and testing. I will not just release it to the Sketchup world, unitl it's tested, proven and approved.)
~

Dan Rathbun

Although == is often overriden in custom subclasses (to do type conversion etc.,) .eql?() is usually not overriden, and retains the original finctionality of the == inherited from the superclass.

Also .equal?() is NEVER overriden! (It's a really big no no.)
~

Jim

moved - ot.

Dan Rathbun

@didier bur said:

Here is my snippet for coplanarity test of 4 points (can be extended to any number of points):

# Given a set of 4 3dPoints, return true if coplanar, or false
> 	def quadPointsCoplanar?(pArray)
> 		return (Geom.fit_plane_to_points(pArray[0],pArray[1],pArray[2]).isEqual?(Geom.fit_plane_to_points(pArray[0],pArray[1],pArray[3])))
> 	end

Will this work to simplify things ?

<span class="syntaxdefault"></span><span class="syntaxcomment"># Given a set of 4 3dPoints, return true if coplanar, or false<br /></span><span class="syntaxdefault">    def quadPointsCoplanar</span><span class="syntaxkeyword">?(</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">)<br /></span><span class="syntaxdefault">        return </span><span class="syntaxkeyword">(</span><span class="syntaxdefault">Geom</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">fit_plane_to_points</span><span class="syntaxkeyword">(</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">0</span><span class="syntaxkeyword">],</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">1</span><span class="syntaxkeyword">],</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">2</span><span class="syntaxkeyword">]).</span><span class="syntaxdefault">eql</span><span class="syntaxkeyword">?(</span><span class="syntaxdefault">Geom</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">fit_plane_to_points</span><span class="syntaxkeyword">(</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">0</span><span class="syntaxkeyword">],</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">1</span><span class="syntaxkeyword">],</span><span class="syntaxdefault">pArray</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">3</span><span class="syntaxkeyword">])))<br /></span><span class="syntaxdefault">    end</span>

I have no problem on Ruby 1.8.6 comparing floats that are very close:
1.0000000001 == 1.0000000002 false 1.0000000001 == 1.0000000001 true

fredo6

I don't think eql? or any float comparison method would work, because the plane defined by [a0, a1, a2, a3] is the same as the one defined by [2 * a0, 2 * a1, 2 * a2, 2 * a3] or any other multiplying factor.

It may be however that Geom.fit_plane_to_points normalizes the returned array, but it is not sure.

So to be on the safe side, both for the precision and for the comparison, I would recommend to compare the planes A[a0, a1, a2, a3] and B[b0, b1, b2, b3] by:

checking if their normals [a0, a1, a2] and [b0, b1, b2] are parallel. SU will answer true or false taking into account the float precision
checking if the first point in the set of points is located on the second plane B.

So, in Dider's example:


def quadPointsCoplanar?(pArray)
   planeA = Geom.fit_plane_to_points pArray[0], pArray[1], pArray[2]
   planeB = Geom.fit_plane_to_points pArray[1], pArray[2], pArray[3]
   normalA = Geom;;Vector3d.new *planeA[0..2]
   normalB = Geom;;Vector3d.new *planeB[0..2]
   normalA.parallel?(normalB) && pArray[0].on_plane?(planeB)
end

Now for 4 points which are different and non-aligned, it is of course easier to do


def quadPointsCoplanar?(pArray)
    planeA = Geom.fit_plane_to_points pArray[0], pArray[1], pArray[2]
    pArray[3].on_plane?(planeA)
end

Fredo

PS to Dan: very instructive your tuto on subclassing, really! Thanks.

Didier Bur

@Dan:
@unknownuser said:

Will this work to simplify things ?
No, it doesn't work.
@all: OK for not adding methods to base classes or SU classes. Module/sub-module stuffs are annoying to code (although the mixin mecanism is fun...) but far more secure.
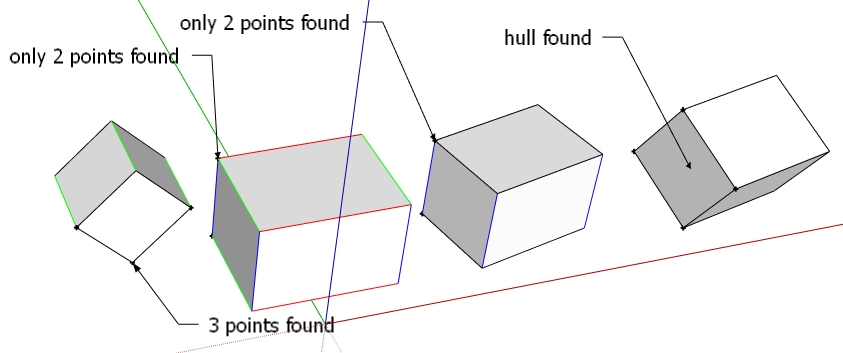
@tt: your Graham's scan works on every common or horizontal face, but not on vertical faces (I mean sets of 4 points that are in a main vertical plane (red-blue), (green-blue), see pic. I suppose that this is due to points having same X and same Y are not sorted correctly. I've tried to apply a transformation to each point before sorting, and apply the inverse transformation after, but no luck.
This transformation was taking the normal of the plane of the 4 points as the Z axis, so the 4 points were virtually in a horizontal plane to be correctly handled by Graham, which is '2D'.)

Dan Rathbun

@didier bur said:

and finaly requires a constant

Math.const_set("EPSILON", 1.0e-10)

I am not sure I agree with this... I do like constants defined in a module that makes sense.

However... is this constant only to be used by your plugin, Didier ?
If so, it needs to be defined inside your plugin submodule, not a Ruby Core module.

If it is to be used by more than one of your plugins, then it should be defined just inside your toplevel module.

Never define global constants that are really your own private constants.

If you wish.. you can create your own Math submodule but it must be defined as Didier::Math or whatever your toplevel namespace is. If you wish your custom Math module to have everthing the standard Math module has, do this:

<span class="syntaxdefault">module Didier<br />  module Math<br />    include</span><span class="syntaxkeyword">(;;</span><span class="syntaxdefault">Math</span><span class="syntaxkeyword">)<br /></span><span class="syntaxdefault">    const_set</span><span class="syntaxkeyword">(</span><span class="syntaxstring">"EPSILON"</span><span class="syntaxkeyword">,</span><span class="syntaxdefault"> 1.0e-10</span><span class="syntaxkeyword">)<br /></span><span class="syntaxdefault">  end<br />end</span>

** The toplevel operator ( **::**) does not work for Ruby 1.8.0

Now any plugin submodule of Didier when it calls Math, will find your nested custom Math module, instead of the standard one up at the toplevel. Example:this:

<span class="syntaxdefault">module Didier<br />  module WizardPlugin<br />    def self</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">epsilon<br />      return Math</span><span class="syntaxkeyword">;;</span><span class="syntaxdefault">EPSILON<br />    end<br />  end<br />end</span>

~

thomthom

@unknownuser said:

checking if their normals [a0, a1, a2] and [b0, b1, b2] are parallel. SU will answer true or false taking into account the float precision

Comparing normals to check if faces where co-planar caused me problems. Doing what Google recommended, taking all the points and checking if they all lie on the same plane has worked great.

Here's what I got from Simone Nicolo:

@unknownuser said:

I'm afraid that comparing 2 unit vectors (within a tolerance of 0.001") is not NEARLY sufficient to determine of two faces are coplanar. Depending on the size of the faces, it is entirely possible (and in fact probable) that two faces with the same face normal (within tolerance) could be highly coplanar (again, within a tolerance of 0.001").

The correct way to check if 2 faces are coplanar is to collect all the vertices of both faces and check that they all lie in a common plane. One can use the method Geom.fit_plane_to_points to compute a best (least squares fit) plane through all the points and then follow that with calls to Geom.on_plane? for each point to verify that all points lie on the computed plane.

Note:this is the way SketchUp determines if 2 faces are coplanar

thomthom

@didier bur said:

@tt: your Graham's scan works on every common or horizontal face, but not on vertical faces (I mean sets of 4 points that are in a main vertical plane (red-blue), (green-blue), see pic. I suppose that this is due to points having same X and same Y are not sorted correctly. I've tried to apply a transformation to each point before sorting, and apply the inverse transformation after, but no luck.
This transformation was taking the normal of the plane of the 4 points as the Z axis, so the 4 points were virtually in a horizontal plane to be correctly handled by Graham, which is '2D'.)

And that didn't work?
hmm... you'd think that;d work.
Did you use Transformation.axes to transform into 2d? Or some other method?

Didier Bur

@unknownuser said:

Did you use Transformation.axes to transform into 2d? Or some other method?

I've used Geom::Transformation.new origin, zaxis

def MyWeirdModule.sort_points_by_x_y_thanks_to_TT(points)
		tpoints=[]
		# normal to the 3 first points of points array
		normalToPointsPlane=Geom;;Vector3d.new(points[0].vector_to(points[1])*points[0].vector_to(points[2]))
		t1=Geom;;Transformation.new(points[0],normalToPointsPlane)
		t2=t1.inverse
		points.each { |p| tpoints.push(p.transform(t2)) }
		tpoints.sort { |a,b| a.x==b.x ? a.y <=> b.y ; a.x <=> b.x }
		return tpoints.each { |p| p.transform!(t1) }
	end

Adding Xaxis and Yaxis to the transformation definition didn't change anything

thomthom

points.each { |p| tpoints.push(p.transform(t2)) }
can be written
tpoints = points.map { |p| p.transform(t2) }

tpoints.sort { |a,b| a.x==b.x ? a.y <=> b.y : a.x <=> b.x }
doesn't do anything - you probably meant .sort!

thomthom

<span class="syntaxdefault"><br />def self</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">sort_points_by_x_y</span><span class="syntaxkeyword">(</span><span class="syntaxdefault">points</span><span class="syntaxkeyword">)<br /></span><span class="syntaxdefault">  v1 </span><span class="syntaxkeyword">=</span><span class="syntaxdefault"> points</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">0</span><span class="syntaxkeyword">].</span><span class="syntaxdefault">vector_to</span><span class="syntaxkeyword">(</span><span class="syntaxdefault">points</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">1</span><span class="syntaxkeyword">])<br /></span><span class="syntaxdefault">  v2 </span><span class="syntaxkeyword">=</span><span class="syntaxdefault"> points</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">0</span><span class="syntaxkeyword">].</span><span class="syntaxdefault">vector_to</span><span class="syntaxkeyword">(</span><span class="syntaxdefault">points</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">2</span><span class="syntaxkeyword">])<br /></span><span class="syntaxdefault">  t1</span><span class="syntaxkeyword">=</span><span class="syntaxdefault">Geom</span><span class="syntaxkeyword">;;</span><span class="syntaxdefault">Transformation</span><span class="syntaxkeyword">.new(</span><span class="syntaxdefault">points</span><span class="syntaxkeyword">[</span><span class="syntaxdefault">0</span><span class="syntaxkeyword">],</span><span class="syntaxdefault">v1</span><span class="syntaxkeyword">,</span><span class="syntaxdefault">v2</span><span class="syntaxkeyword">)<br /></span><span class="syntaxdefault">  tpoints </span><span class="syntaxkeyword">=</span><span class="syntaxdefault"> points</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">map </span><span class="syntaxkeyword">{</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">|</span><span class="syntaxdefault">pt</span><span class="syntaxkeyword">|</span><span class="syntaxdefault"> pt</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">transform</span><span class="syntaxkeyword">(</span><span class="syntaxdefault">t1</span><span class="syntaxkeyword">)</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">}<br /></span><span class="syntaxdefault">  tpoints</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">sort</span><span class="syntaxkeyword">!</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">{</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">|</span><span class="syntaxdefault">a</span><span class="syntaxkeyword">,</span><span class="syntaxdefault">b</span><span class="syntaxkeyword">|</span><span class="syntaxdefault"> a</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">x</span><span class="syntaxkeyword">==</span><span class="syntaxdefault">b</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">x </span><span class="syntaxkeyword">?</span><span class="syntaxdefault"> a</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">y </span><span class="syntaxkeyword"><=></span><span class="syntaxdefault"> b</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">y </span><span class="syntaxkeyword">;</span><span class="syntaxdefault"> a</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">x </span><span class="syntaxkeyword"><=></span><span class="syntaxdefault"> b</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">x </span><span class="syntaxkeyword">}<br /></span><span class="syntaxdefault">  tpoints</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">map</span><span class="syntaxkeyword">!</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">{</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">|</span><span class="syntaxdefault">pt</span><span class="syntaxkeyword">|</span><span class="syntaxdefault"> pt</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">transform</span><span class="syntaxkeyword">(</span><span class="syntaxdefault"> t1</span><span class="syntaxkeyword">.</span><span class="syntaxdefault">inverse </span><span class="syntaxkeyword">)</span><span class="syntaxdefault"> </span><span class="syntaxkeyword">}<br /></span><span class="syntaxdefault">end<br /></span>

Didier Bur

Given 3 points:
v1 = points[0].vector_to(points[1])
v2 = points[0].vector_to(points[2])
t1=Geom::Transformation.new(points[0],v1,v2)
-> the transformation that put any face containing these points in the red-green plane is t1.inverse (I've drawn it to be sure)

So why does't Graham's scan work for such a face, once put on the main horizontal plane ?
I've typed: 'puts l_upper.length,l_lower.length' in self.convex_hull method. It always end up with 2 and 0 respectively.
Is the "guilty" self.right_turn?
It's just (one more time) a question of tolerance I guess. I've output the determinant value and it is sometimes, say -5.6843418860808e-014 and sometimes exactly 0.0
Maybe something to search here...

Another thing: convex hull is sometimes correct for any horizontal face at a z!=0, but always incorrect when the face is at z=0.
I tested a horizontal face with z!=0 and got a convex hull of 2 points. I erased that face and redraw it exactly the same, then the convex hull was correct (4 points). I made a copy of the correct face upward and again the hull was incorrect, go figure. Pffff, I'm really puzzled, after all...

Didier Bur

Starting graham's hull from scratch, it works now. Thanks go to TT, mostly

thomthom

@didier bur said:

Starting graham's hull from scratch, it works now. Thanks go to TT, mostly

It works on any plane now?

Didier Bur

Yep, on any plane

Here is the rough test code: make a selection of n coplanar guide points on any face, type 'graham' in the console and it draws the convex hull correctly. As you will see, code is yours almost entirely. It's likely there is something wrong in my classes or methods.

def graham()
	pts=[]
	# Selection of coplanar guide points to array pts
	Sketchup.active_model.selection.each { |cp| pts.push(cp.position) }
# Transform points to horizontal plane
	t1=Geom;;Transformation.new(pts[0],pts[0].vector_to(pts[1]),pts[0].vector_to(pts[2]))
	horizPoints = pts.map { |pt| pt.transform(t1.inverse) }
	# Sort by X and Y
	points = sort_points_by_x_y(horizPoints)
	# Graham
	l_upper = [ points[0], points[1] ]
	2.upto(points.length - 1) do |i|
		l_upper << points[i]
		while l_upper.length > 2 && !right_turn?(l_upper.last(3))
			l_upper.delete_at(-2)
		end
	end

	l_lower = [ points[-1], points[-2] ]
	(points.length - 3).downto(0) do |i|
		l_lower << points[i]
		while l_lower.length > 2 && !right_turn?(l_lower.last(3))
			l_lower.delete_at(-2)
		end
	end
	l_lower.delete_at(0)
	l_lower.delete_at(-1)
	# Reset convex hull to its original transform
	hull=(l_upper + l_lower).map! { |pt| pt.transform(t1) }
	# draw hull
	Sketchup.active_model.entities.add_line(hull)
	Sketchup.active_model.entities.add_line(hull.last,hull.first)
end

def right_turn?(points)
	p, q, r = points
	return (determinant_3x3([1,p.x,p.y,1,q.x,q.y,1,r.x,r.y]) < 0.0)
end

def determinant_3x3(array)
	a,b,c,d,e,f,g,h,i = array
     return ((a*e*i) - (a*f*h) + (b*f*g) - (b*d*i) + (c*d*h) - (c*e*g))
 end
	 
def sort_points_by_x_y(points)
	return points.sort! { |a,b| a.x==b.x ? a.y <=> b.y ; a.x <=> b.x }
end