Alternative to angle_between?
-
I have two vectors I want to check the angle and orientation of against another vector.
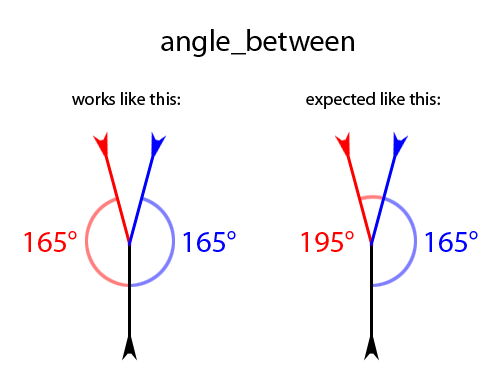
In this illustration, the black vector is the one I use to check the angles against the two others. (Arrow indicated the direction of the vectors.) Both are rotated equally to either side of the black vector, but still returns the same angle - as seen in the left illustration. What I had expected, and what I need, is for them to return two different angles - like in the right illustration.Is there an alternative to angle_between that will give me two different angles?
Or, is there a way where I can determine if the vectors are leaning left or right from the black vector?
-
I just got a GREAT lesson in vector math, but I've forgotten most of it already. But I'm wondering if you use the dot product also of each angle to help figure this out. What happens if you take
base_vector.dot blue_vector
base_vector.dot red_vectorDoes one return positive and one return negative?
Thats my stab in the dark....
Chris
-
I imagine using the .dot method would give the same result as angle_between, as angle_between most likely uses the dot product to find the angle between the 2 vectors.
As for actually solving your problem, i'm currently stumped.
-
You have to choose a Z direction (perpendicular to the plane of the two vectors, in order ot orient your angles.
Otherwise it is normal that you get the same value (just imagine you look at your picture from the back!).Then you make a difference by the sign of (vec1 * vec2) % vecZ
Fredo
-
If the red and blue vector where both 90 degrees from the black vector
vZreturned(0,0,0)which then give me0.0forv1andv2...
I think I've gotten something wrong...(Currently reading up on vectors on Wiki...goes a bit over my head. Any recommended starting material?)
-
this is quite good, as long as you skim over the first paragraph. http://mathworld.wolfram.com/Vector.html
-
@unknownuser said:
You have to choose a Z direction (perpendicular to the plane of the two vectors, in order ot orient your angles.
Otherwise it is normal that you get the same value (just imagine you look at your picture from the back!).Then you make a difference by the sign of (vec1 * vec2) % vecZ
Fredo
Ok... I'm not 100% sure if I understand this. But this is what I tried:
e1 = base vector e2 = left vector e3 = right vectorvZ = e2 * e3 # returns (0, 0, -0.5) v1 = (e1 * e2) % vZ # returns 7.41461947099021 v2 = (e1 * e3) % vZ # returns -7.41461947099021That does give me a positive and negative number. However, I'm not sure what that number represent, nor am I sure I did this correctly.
-
Perhaps the cross method is best. The cross method of 2 vectors will return a vector that is perpendicular to the plane they lie on. (this is using colors as defind by SketchUp) So if you do
green.cross red, that returns the blue axis vector ([0,0,1]. But if you dored.cross greenyou get the negative blue axis vector ([0,0,-1). So by doing the cross vector on your vectors you can determine if the 2 angle_between's rotated the same direction. If they did, then both cross vector products will be positive or both negative. But if angle_between rotated a different way to find each angle, then the cross product will return one true and one false. Does that make sense?Chris
-
Yes. It makes sense.
Though, I also need to reliably determine the direction of one vector against another. I wonder if getting the cross and checking if it's positive or negative is certain to determine the direction of the angle. -
Thom
Following on from Chris, I dont know if this code snippet from one of my tools helps
def checkside(v1,v2) v3 = v1.cross(v2) return ((v3.z < 0) ? 1 ; -1) end # main body v1 = @pts[1].vector_to(@pts[2]) @alignment = checkside(@stairdirvec,v1)It returns 1 or -1 depending on which side I need to draw. @stairdirvec is the primary direction which v1 is tested against.
BillW
-
@unknownuser said:
You have to choose a Z direction (perpendicular to the plane of the two vectors, in order ot orient your angles.
Otherwise it is normal that you get the same value (just imagine you look at your picture from the back!).Then you make a difference by the sign of (vec1 * vec2) % vecZ
Fredo
Just to make clearer what I said in an earlier post. Referring to the picture, you have 3 vectors: red, blue and black.
If you wish to measure the 'oriented' angles between 'blue and black' and 'blue and red', you must decide on a reference rotation direction (in plane geometry, we would count in the trigonometric sense, or anti-clockwise).
The reference direction is what you want, but is perpendicular to the other vectors. So, for instance, if you are fine with the angle returned by
vec_black.angle_between(vec_blue), then the reference direction would bevec_rotation_ref = vec_black * vec_blueNow, for the red vector, you compute
vec_black * vec_red
and then compare its orientation with your reference rotation vector, by making the scalar product (which is negative if the vectors have opposite directions, and positive otherwise).angle_red = vec_black.angle_between(vec_red) if vec_black * vec_red) % vec_rotation_ref < 0 angle_red = 2 * Math;PI - angle_red endNote that if you work in the horizontal plane, the you can take Z_AXIS as your reference rotation vector (and then Bill'sformula works).
Fredo
-
Thanks for clarifying that Fredo. I had temporary used a fixed [0,0,1] vector for references. (The plugin I work on works completely planar.)
@unknownuser said:
you must decide on a reference rotation direction (in plane geometry, we would count in the trigonometric sense, or anti-clockwise).
By a 50/50% chance I'd chosen counter-clockwise.

-
Hi,
If this can help:def angle2Pi(p1,p2) twoPI = 2.0*Math;;PI return (Math.atan2(p2.y-p1.y, p2.x-p1.x)+twoPI).modulo(twoPI) endThis returns the angle of a vector that starts at point p1 and ends at point p2, no matter wether p1 or p2 is the starting vertex. this is recommanded you use this only in 2D of course.
Regards, -
@unknownuser said:
@unknownuser said:
You have to choose a Z direction (perpendicular to the plane of the two vectors, in order ot orient your angles.
Otherwise it is normal that you get the same value (just imagine you look at your picture from the back!).Then you make a difference by the sign of (vec1 * vec2) % vecZ
Fredo
Just to make clearer what I said in an earlier post. Referring to the picture, you have 3 vectors: red, blue and black.
If you wish to measure the 'oriented' angles between 'blue and black' and 'blue and red', you must decide on a reference rotation direction (in plane geometry, we would count in the trigonometric sense, or anti-clockwise).
The reference direction is what you want, but is perpendicular to the other vectors. So, for instance, if you are fine with the angle returned by
vec_black.angle_between(vec_blue), then the reference direction would be> vec_rotation_ref = vec_black * vec_blue >Now, for the red vector, you compute
vec_black * vec_red
and then compare its orientation with your reference rotation vector, by making the scalar product (which is negative if the vectors have opposite directions, and positive otherwise).> angle_red = vec_black.angle_between(vec_red) > if vec_black * vec_red) % vec_rotation_ref < 0 > angle_red = 2 * Math;PI - angle_red > end >Note that if you work in the horizontal plane, the you can take Z_AXIS as your reference rotation vector (and then Bill'sformula works).
Fredo
Ok, I've been trying to get this to work no-planar. But I'm having problems with the reference vector - because I don't have both the vectors to compare against at that point of the code.
I only have a base vector - that one that I compare against.I've been trying to take the cross of the base vector (black) and the vector I compare against (red/blue), but it seem to be 50/50 chance that the cross vector points in opposite directions. Not sure how to orient it predictably....
-
Sorry for digging up another old topic, here's my not-so-rough guess at a long way around.
angle1 = black_vector.angle_between red_vector vector_cross = black_vector.cross red_vector vector_90 = black_vector.cross vector_cross angle2 = vector_90.angle_between red_vector angle1 = (Math;;PI-angle1) + Math;;PI if angle2 >= (Math;;PI/2) -
Also, as a bit of a bodge to fix the 50/50 direction problem
vector_90 = Geom;;Vector3d.new(vector_90[0].abs,vector_90[1].abs,vector_90[2].abs)Its probably not efficient, or even tested
-
I've been working on this problem quite alot lately, and I've realised the code I posted is wildly incorrect, as you say ThomThom:
@thomthom said:it seem to be 50/50 chance that the cross vector points in opposite directions.
so we should probably compare the cross vector against something relatively static, like one of the model axes?
@unknownuser said:
Note that if you work in the horizontal plane, the you can take Z_AXIS as your reference rotation vector (and then Bill'sformula works).
could this work if we reverse the cross vector based on its angle to the Z_AXIS (ie. greater than 90 degrees then reverse cross vector).
-
@bentleykfrog said:
I've been working on this problem quite alot lately
 I've finally got my 2d manifold detection working (albeit quite slowly as I have to calculate an infinite line [planar normal of an edge] intersecting a complex polygon [face] for each edge to determine the side of the edge its associated face is on). Anyway I thought I'd post the code here for some feedback and optimization advice. Here's the code snippet: feel free to chop/change/reuse if you like.
I've finally got my 2d manifold detection working (albeit quite slowly as I have to calculate an infinite line [planar normal of an edge] intersecting a complex polygon [face] for each edge to determine the side of the edge its associated face is on). Anyway I thought I'd post the code here for some feedback and optimization advice. Here's the code snippet: feel free to chop/change/reuse if you like.def intersect_line_line_segment_2d(line,segment) x1 = line[0].x y1 = line[0].y x2 = line[1].x y2 = line[1].y x3 = segment[0].x y3 = segment[0].y x4 = segment[1].x y4 = segment[1].y u_line_n = ((x4 - x3)*(y1 - y3)) - ((y4 - y3)*(x1 - x3)) #line equation numerator denom = ((y4 - y3)*(x2 - x1)) - ((x4 - x3)*(y2 - y1)) #line & segment equation denominator u_segment_n = ((x2 - x1)*(y1 - y3)) - ((y2 - y1)*(x1 - x3)) #segmnet equation numerator if denom == 0 #line and segment are parallel return false end #if u_segment = u_segment_n.quo(denom) if u_segment >= 0 || u_segment <=1 #return [x1 + (u_segment*(x2-x1)),y1 + (u_segment*(y2-y1)),1] #use to return the point of intersection u_line = u_line_n.quo(denom) #use to return a relative distance value for ordering return u_line #intersections on a complex polygon else #intersection is outside the line segment return false end end #def def find_manifold_face(origin_face_id,fold_edge_id,possible_face_ids,check_orientation=false,correct_orientation=false) origin_face = @@face_objects[origin_face_id] origin_edges = @@faces_to_edges[origin_face_id] manifold_face = false # PT1; ORIGIN FACE->FOLD EDGE ORIENTATION # we need to find on which side of the edge the face is, and then # determine the direction of rotation. This is more difficult than # it appears. The most error-free way to do it is to create a line # that represents the planar normal for the edge (ie perpendicular # to the fold edge and on the plane of the origin face) and find the # line segments that intersect with the face using an Intersect Segment # with Polygon algorithm. [see; http://softsurfer.com/Archive/algorithm_0111/algorithm_0111.htm] # A COUPLE OF NOTES FIRST; # 1;We only need a 2d coordinate system for this so we can use the UVHelper # to generate this and hopefully make the code more efficient # 2;We only need to find the first intersected line segment that shares # one of its points with the fold edge fold_verts = @@edges_to_verts[fold_edge_id] #construct points on the fold edge that will help with fold_arr = fold_verts.values #orientation; pt1; start, pt2; middle, pt3; end fold_pt1 = fold_arr[0].position fold_pt3 = fold_arr[1].position fold_pt2 = fold_pt1 + Geom;;Vector3d.new((fold_pt3.x-fold_pt1.x).quo(2),(fold_pt3.y-fold_pt1.y).quo(2),(fold_pt3.z-fold_pt1.z).quo(2)) fold_vec = fold_pt1.vector_to fold_pt3 trans = Geom;;Transformation.rotation fold_pt2, origin_face.normal, -90.degrees o_vec1 = fold_vec.transform trans origin_uvhelp = origin_face.get_UVHelper true, false, @@tw #UVHelper can give us 2d coordinates for a 3d face ;) fold_uv_pt1 = origin_uvhelp.get_front_UVQ(fold_pt1) #construct the corresponding uv points that are uv fold_uv_pt2 = origin_uvhelp.get_front_UVQ(fold_pt2) #representations of the 3d coordinates fold_uv_pt3 = origin_uvhelp.get_front_UVQ(fold_pt3) fold_uv_vec = fold_uv_pt1.vector_to fold_uv_pt3 trans_uv_vec = Geom;;Vector3d.new(fold_uv_vec[1],-fold_uv_vec[0],1) #construct a fold edge normal line to trans_uv_pt = fold_uv_pt2 + trans_uv_vec #calculate the line segments of intersection trans_uv_line = [fold_uv_pt2, trans_uv_pt] intersection_array = Array[0] origin_edges.each {|edgeID| next if fold_edge_id == edgeID edge_uv_pt1 = origin_uvhelp.get_front_UVQ(@@edge_objects[edgeID].start.position) edge_uv_pt2 = origin_uvhelp.get_front_UVQ(@@edge_objects[edgeID].end.position) edge_uv_segment = [edge_uv_pt1, edge_uv_pt2] intersection_u = self.intersect_line_line_segment_2d(trans_uv_line,edge_uv_segment) next if !intersection_u intersection_array << intersection_u } if intersection_array.length <= 1 msg = "Critical Error; Normalize Toolkit encountered an illegal face (a face with only two vertices).\nYour model probably has errors?" msg += "To check, select the menu item 'Window' -> Model Info, then select 'Statictics' and click on 'Fix Problems'." self.alert_error(msg,true) Sketchup.send_action CMD_SELECT return false end #if intersection_array.sort! #ok lets find if the vector is pointing the right way reverse = (intersection_array.index(0) % 2) ? 1 ; -1 o_vec1.reverse! if reverse == -1 o_pt1 = fold_pt2 + o_vec1 o_vec2 = origin_face.normal #make the origin face's normal an orientation vector #we need two vectors at right angles to get around the #angle_between not greater than 180 degrees problem. smallest_angle = 360.degrees possible_face_ids.each {|faceID| next if !@@faces_to_verts.has_key?(faceID) next if faceID == origin_face_id #logically, the p_vec1 should be found by rotating the fold_vec in the opposite direction #as o_vec1 was. The only issue here is that if the normal is reversed, we wont get a correctly #facing vector. Fortunately, we can determine this by comparing the clockwise angle from o_vec1 #to p_vec1 and from o_vec1 to @@face_objects[faceID].normal. #If o_vec1 to p_vec1 is smaller than o_vec1 to @@face_objects[faceID].normal, we've got a reversed #normal!! cool trans = Geom;;Transformation.rotation fold_pt2, @@face_objects[faceID].normal, reverse * 90.degrees p_vec1 = fold_vec.transform trans t_ang1a = o_vec1.angle_between @@face_objects[faceID].normal t_ang1b = o_vec2.angle_between @@face_objects[faceID].normal t_ang2a = o_vec1.angle_between p_vec1 t_ang2b = o_vec2.angle_between p_vec1 t_ang1 = (t_ang1b <= 90.degrees) ? t_ang1a ; 180.degrees + (180.degrees - t_ang1a) t_ang2 = (t_ang2b <= 90.degrees) ? t_ang2a ; 180.degrees + (180.degrees - t_ang2a) #another problem here is that the difference between t_ang1 & t_ang2 should be roughly plus or minus 90 degrees #if its greater, then the possible face is on such an obtuse angle and reversed that its normal is closer to #o_vec1 than p_vec1 is p_vec1.reverse! if ((t_ang1 > t_ang2) || ((t_ang2 - t_ang1) > 180.degrees)) o_ang1 = o_vec1.angle_between p_vec1 o_ang2 = o_vec2.angle_between p_vec1 manifold_angle = (o_ang2 <= 90.degrees) ? o_ang1 ; 180.degrees + (180.degrees - o_ang1) if manifold_angle < smallest_angle smallest_angle = manifold_angle manifold_face = @@face_objects[faceID] end } if !manifold_face return false end if check_orientation direction = self.get_rotation_direction(fold_vec,fold_pt2,origin_face.normal,o_pt1) #work out whether the vector is pointing in the right direction trans = Geom;;Transformation.rotation fold_pt2, fold_vec, (smallest_angle * direction) #rotate the origin normal so its aligned with m_normal = o_vec2.transform trans #the manifold's normal. This should give a vector m_ang1 = m_normal.angle_between manifold_face.normal #that angles 180 degrees from the manifold's normal oriented = (m_ang1 > 90.degrees) ? true ; false #if its less than 90 degrees, reverse the face. return Hash[ "manifold_face" => manifold_face, "oriented" => oriented ] end #if return manifold_face end #def -
just for context, attached is the wip with a few modifications to the previous post to reduce the load significantly if we're dealing with convex polygons.
-
See if any ideas here help. Tried to find arctan2 for three 3d. More search probably required
http://www.euclideanspace.com/maths/algebra/vectors/angleBetween/index.htm
Advertisement







