Horisontal AOV?
-
Camera.fovreturns the vertical AOV. But how do I get the horizontal or diagonal AOV?From Wiki I find this forumla: http://en.wikipedia.org/wiki/Angle_of_view
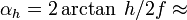
(
Math.atan== arctan, right?)Problem is, that assumes a film width and height... Which I don't have for the SU camera. So, how do you go about calculating the various AOV?
-
Also, since my trigonometry isn't the best, if you have a plane at the camera's target distance parallel with the camera, how would you plot the four camera corners onto it? I have a feeling I'm not trying to calculate this in the most efficient way...
-
The up/down/left/right dimensions of this 'square' away from the target that would superimpose onto the target-plane, from the target itself across the target-plane are found thus:
=distance_from_camera_to_target * Math::tan(fov.degrees / 2)
Assuming that the camera is looking horizontally then you can easily calculate the corners of this square setting each away from the target point on the plane.
If the camera has been rotated then you'll need to rotate transform these points to match... -
@tig said:
The up/down/left/right dimensions of this 'square' away from the target that would superimpose onto the target-plane, from the target itself across the target-plane are found thus:
=distance_from_camera_to_target * Math::tan(fov.degrees / 2)
Assuming that the camera is looking horizontally then you can easily calculate the corners of this square setting each away from the target point on the plane.
If the camera has been rotated then you'll need to rotate transform these points to match...But how do I get the horizontal FOV?
-
Surely the basic fov is equal in both directions ? If you have different lenses there's a proportional relationship to the window's edges...
-
AOV is more correct. (SU calls it fov, but it's really AOV)
And the vertical and horizontal and diagonal AOV is not equal. -
Thom, you can get the width and height of the screen with view.corner. Does that help?
point = view.corner index
and index = 0,1,2,3 for the 4 corners of the screen.
Or does the aspect ratio not help with AOV and FOV. I need a bit of a lesson in cameras.
Chris
-
view.corner *x*returns a Line [Point3D, Vector3D]. No dimensions. However, I did use it to intersect the lines with a plane parallel to the camera located at the camera's target point. With that, I could draw the frustum, which was one thing I wanted to do.
However, I'm not sure if that's the most efficient way.Also, I tried getting the ratio of the viewport width / height and using that ratio to multiply with the vertical AOV (.fov) that SU returns. But the value I get isn't right.
I'm also not that familiar with cameras and how they operate. And certainly not the SU camera. So between that and my poor trigonometry and general knowledge of 3D geometry concepts I'm fumbling along somewhat in the dark...
-
Hmm, for me it is returning the x and y positions, not a line.
model = Sketchup.active_model
view = model.active_view
point = view.corner 3
puts "#{point[0]} x #{point[1]}"that will put the width and height of the drawing area. If you know that, and the AOV, couldn't you calculate the FOV (assuming you can get your trigonometry to agree with you (my #1 problem also....grrr)).
Chris
EDIT: I tihnk I misunderstood what the AOV was....perhaps its not as simple as I thought. I'll keep playing with it for a little bit too.
-
Sorry. My last post way lying.
.corner returns a 3DPoint with only x & y populated, yes. I confused it with .pickray.The thing is, I'm not trying to find the FOV, but I want the Horizontal AOV. (That's not the FOV, is it? I'm a bit confused about 'FOV'.) From what I understand, what SU calls .fov is the vertical AOV...
-
Well don't forget the PC camera tool
Sketchup.send_action 10624and don't forget to use the film and stage plugin. That is always useful to help visualize exactly where the phsical camera is located.
-
@chris fullmer said:
Well don't forget the PC camera tool
Sketchup.send_action 10624Yea, I use that for debugging.
@chris fullmer said:
and don't forget to use the film and stage plugin. That is always useful to help visualize exactly where the phsical camera is located.
hm... yea. I could have a look at what that does. I've never used it though.
At the moment I manage to draw the viewing frustum so I know exactly where it is. But I want to take it further and make some tools to manipulate the camera. And for that I need to work out the AOV in all possible directions...
I'm reading up on real cameras and how they work. But I'm having some trouble applying that to the SU camera.
-
Ok, so I'm digging around too and it appears that AOV and FOV are virtually identical, they are just represented differently.
@unknownuser said:
Although related, FOV is not exactly the same as angle of view; FOV is measured in linear, spatial dimensions (feet, inches, metres, etc) whereas AOV (more properly called the angular field of view) is measured in degrees of arc. FOV increases with distance, whereas AOV does not. FOV changes as the camera rotates, AOV does not.
and another good one, using the specs of a 50mm lens:
@unknownuser said:
At a working distance of 10 metres, the horizontal field of view is therefore 7.2 metres; at a distance of 100 feet, the horizontal field of view is 72 feet, etc. (The horizontal AOV is about 39.6º at any distance)
So it appears they are identical in value, just the FOV changes based on the distance away from the camera you are talking about.
Chris
-
This is why I think SU mixes up the terms FOV and AOV. Because in the Camera Debug window you have Fov(H) and Fov(W) - both two different values. By default Fov(H) is enabled.
-
FOV(H) is the angle of view (AOV) from top to bottom where FOV(W) is the AOV from side to side.
So yes, its confusing. I think I just got the trig worked out to solve it all. Let me put it together so it works and I'll post what I have, in case it helps.
Chris
-
Thanks for looking into this.
I want to be able to make a tool where the AOV can be set in Horizontal, Vertical or Diagonal direction. So I need to be able to work this out. -
the fov of a real camera is a function of the film frame dimensions. It is commonly related to a standard film with frames of 3624 mm - a 50 mm lens over a 3624 mm film frame is not the some of a 50 mm lens over a 60*60 mm film frame.
i know, it's a bit confusing. all the new digital cameras have show an equivalent fov: that's because it would be too tricky to figure out the real angle of view, since there are somany formats. for more informations give a look to this on wikipedia: http://en.wikipedia.org/wiki/Image_sensor_format
talking about the aov, it is not so difficult to find the horizontal angle when you have the vertical angle values and the aspect ratio.
if you look at the first image, I extract half horizontal aov (1/2 Haov by now) + half vertical aov (1/2 Vaov by now) and unfold them.
we have now quite a simple trigonometric problem. both triangles, blue and yellow, share the some radius: then 1/2 Haov tangent is equal to half screen length - and 1/2 Vaov is equal to 1/2 screen heigth. see figure two.
now the formula is quite simple to obtain
1/2 Haov = arctan [tan(1/2 Vaov)*(length/heigth)]
let's suppose that you have a Vaov of 60° and a screen aspect ratio of 3/2, the Haov is equal to:
Haov = 2* arctan [tan(60°/2)(3/2)] = 2 arctan [tan(30)1,5] = 2 arctan (0,577351,5) = 2 arctan (0,866025) = 2* 40,89339° =
81,786789°
i hope this can help you thom
note: all angles are measured in degrees and not radiants or else./matteo bignozzi
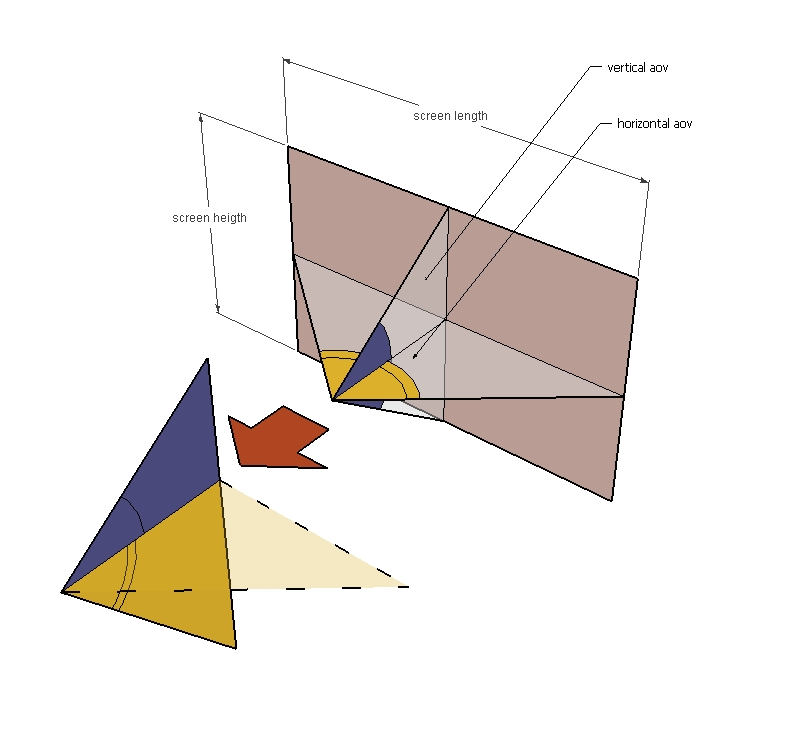
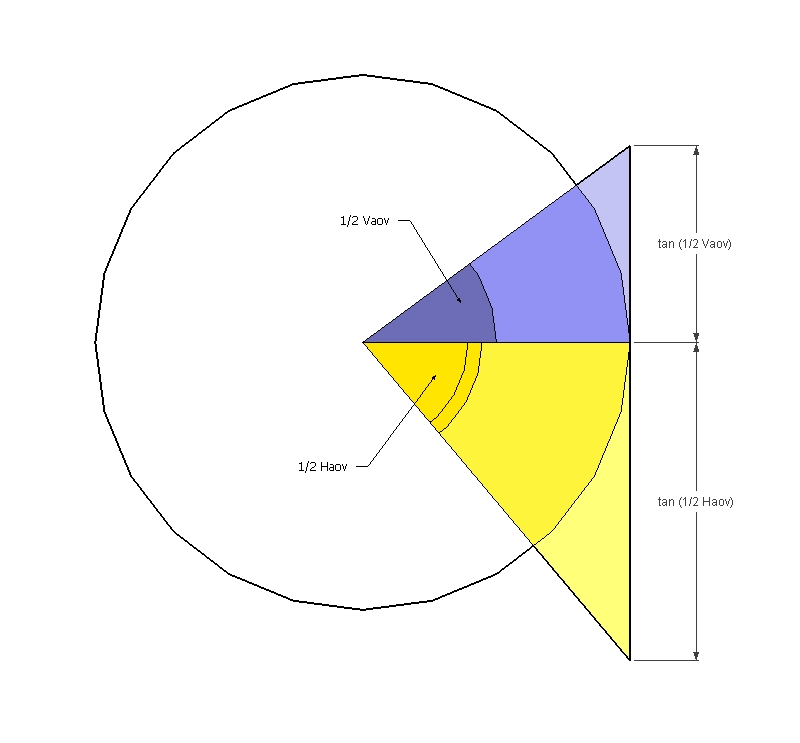
-
It worked!
The true test to if I understood this will be when I try to make functions that calculate between all directions of Vaov, Haov and Daov. At least I can go to bed now.

-
Oh good. have you got it all worked out then in Ruby Thom?
Chris
-
def self.haov_from_vaov(vaov, ratio) return (2 * Math.atan( Math.tan(vaov.degrees / 2) * ratio )).radians endWhen (if) I get the other conversions worked out I'll post them back here in case anyone else should need them. (Plus, people with better math skills than me can verify if I did it right...
 )
)
Advertisement







