How do you calculate the base of an Isosceles Triangle?
-
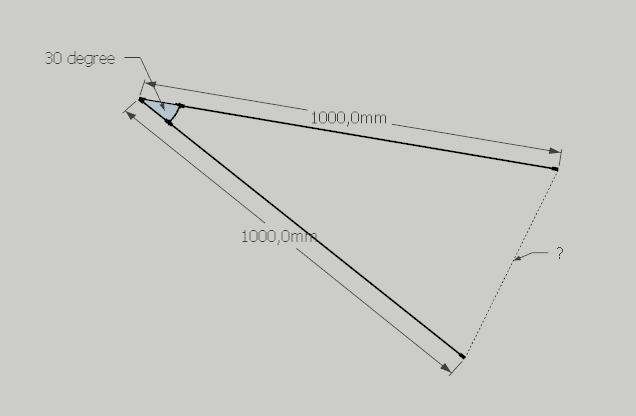
I'm in need of a math refresher course. I'm working on a DC component where I need to find out the forumla to calculate the length of the base of an Isosceles Triangle when I have the length of the two equal sides and the angles of the corners.
I've been searching around for trigonometry and triangle formulas but I just can't wrap my head around it.
-
2side lengthsin(angle/2)
Got the formula by splitting the triangle down the middle to get 2 right angle triangles. You can then use standard trig on it ( i.e. sin(angle)=opposite/hypotenuse), although this only finds half the base, so you need to add the *2 in to compensate.
Hope thats helpful.
-
Hmm... The result I get from that is 1300,57568 which is the same result I get from using the Law of Cosine from http://en.wikipedia.org/wiki/Law_of_cosines
But the measured length is 518mm... Maybe I'm writing the formula wrong.
I use Excel to test the formula, and this is what I typed in:
=2*1000*SIN(30/2) -
btw, the formula I used based on the Wiki article is:
=SQRT(B1^2 + B2^2 - (2*B1*B2*COS(B4)))which I optimised for Isosceles Triangles by changing to:
=SQRT(2*B1^2 - 2*B1^2*COS(B4))where B1 and B2 is the side lengths and B4 is the angle. Both give same result as Remus's formula, but yet not the actual length of the unknown side.
...I can hear the joint laughter of my old math teachers with the echo of myself "I'll neverhave use for that in real life!"

-
On my calcualtor I enter
15
sin
X
1000
X
2and I got:
517.6380902050415246977976752481 -
I think the sin function must be in radians.
If you can get the angle in radians, then just put that in instead, otherwise use this formula instead:
=2*side length*sin((angle*pi)/360) -
@remus said:
I think the sin function must be in radians.
If you can get the angle in radians, then just put that in instead, otherwise use this formula instead:
=2*side length*sin((angle*pi)/360)That was it! That's the reason it didn't work!
gaaah... and I was thinking that I'd missed something in the understanding of the formula.
Thankyou Remus!
-
And what's more: had I tried it directly in SU I wouldn't have had that problem because the SIN function then sakes degrees and not Radians... doh!
Advertisement







