Request plugin :Trilateration ruby
-
Dear Ruby programmers,
Sketchup is still missing a very simple basic tool that would be very useful to many users.
There is no way to precisely draw a triangle with known side-lengths.(= Trilateration).
A Triangle ruby could do that.
It could function as follows.You first activate the triangle ruby.
You would be prompted to draw the first line of the triangle the normal way.
Then the sticky sort of help-line at your cursor with its origin from the first line should appear to let you choose the plane the triangle should be drawn on.
At the same time you should be prompted to fill in the value control box with the two remaining side-lengths of the triangle (counter clockwise?) probably separated with ; .
After the Enter command these lines would be drawn.Could some of you please make this ruby?
Greeting,
Bep van Malde
-
You can sort of do this with the polygon tool, just set the number of sides to 3...
If you need irregular triangles, you could then just alter it with the move tool, and with some simple maths you could have pretty much any triangle that takes your fancy.
-
@remus said:
You can sort of do this with the polygon tool, just set the number of sides to 3...
If you need irregular triangles, you could then just alter it with the move tool, and with some simple maths you could have pretty much any triangle that takes your fancy.
Yes Remus i know it is possible this way and probebly some other ways ,but they are all to cumbersome doing this many-many times ,or to complicated.
I realy would like to skip the math and let the ruby do all of that time after time. -
Dear Bep,
You can make an equilateral triangle of known side length using the following method:
Use the polygon tool with the number of sides set to 3
Draw a triangle
Double click to select all the entities and make a group
Double click to edit the group, and when in edit mode use the tape measure tool to measure one side
Type in the desired length
Type yes when asked about resizing group
Explode groupRegards,
Bob -
@watkins said:
Dear Bep,
You can make an equilateral triangle of known side length using the following method:
Use the polygon tool with the number of sides set to 3
Draw a triangle
Double click to select all the entities and make a group
Double click to edit the group, and when in edit mode use the tape measure tool to measure
one side
Type in the desired length
Type yes when asked about resizing group
Explode groupRegards,
BobThank you Bob for responding,
But the ruby i request could help to contruct all types of triangles ,scalene if no sides are equal;isosceles if two sides are equal;equilateral if three sides are equal.
greetings ,
Bep van Malde
-
-
On my to-do-list[/quote]
Thank you Didier, that you are taking up an interest in developing this Ruby.
I am very happy
I can now rest asure knowing that it will be made.Greetings,
Bep van Malde
-
@Bep,
Just a question: Given Side1 from Point A to Point B, and 2 lengthes a and b, the general trilateration case (from Al-Kashi theorem) gives 4 solutions.How do you would see the script determine which triangle is the "good" one (from the user point of view I mean) ?
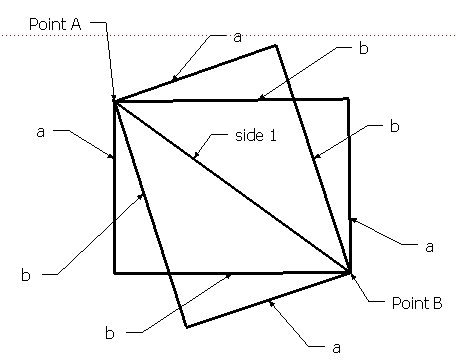
-
What if you allow all four - separately grouped - and let the user delete the unwanted ones.
But also, what would decide which plane they are drawn? In 3D space there are endless possibilities. Or would you then restrict it to the red/green axis? Or maybe not if the initial line is drawn on any face?
-
Ah, I see, the plane has been solved. Yes, logical. Also the solution for the choice of the triangles sounds quite reasonable!
-
What is currently on the drawing board is:
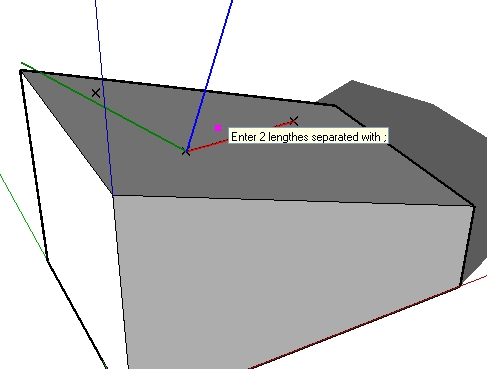
User clicks 2 points to define the first side of the triangle (the red line between the 2 "X"), and click 1 point to define the plane (the third "X"). The plane is computed with a crossproduct between vectors, this is not a problem.
Between the 4 possibilities still remaining, I would suggest that the first length entered would start from the start point of side 1, the second would start from end point of side 1. This leads to 2 solutions. So I also suggest that the point defining the plane will also define the pointing direction of the second side (given by the first length) to get only one solution.
What do you think ? -
Didier,
You are much faster than I am.
I think that we come up with the same sort of solution.Bep
-
Bep,
I'll PM you soon a beta for test. It's almost ready, just several weird angle problems to solve
Regards, -
I can hardly wait!

Advertisement







