@ Régis: t'as tout bon !
Posts
-
RE: Création de surfaces "mathématiques" ?
@ Pilou: merci pour l'exemple avec K3dsurf, je vais m'y repencher, car j'appréciais bien la manière de se promener au sein de l'image...
@ Régis: les 3 équations que tu mets en exemple n'ont rien à voir entre elles, si ce n'est leur ressemblance dans l'écriture, mais qui ne se traduit pas sur leur comportement "mathématique"; donc leur graphe sont totalement indépendants. Ce n'est donc pas "3 fois la même formule (ou presque)".
Effectivement, pour pouvoir exploiter les coupes des surfaces, il faut d'abord avoir une bonne représentation des graphes d'une fonction d'une variable (genre x^2, x^3, x^4,1/x, sin(x), cos(x), tan(x), etc...).
Quelques petits exercices...
@+
-
RE: Création de surfaces "mathématiques" ?
J'avais testé kdsurf, mais je ne suis pas parvenu à l'exploiter; il me semble que son but est la représentation d'hyperespaces de dimension supérieure ou égale à 4...
-
RE: Création de surfaces "mathématiques" ?
Pour avoir des exemples concrets, voici un lien parmi d'autres (il y en a vraiment beaucoup):
http://www.mathcurve.com/surfaces/surfaces.shtml
Bonnes découvertes ! -
RE: Création de surfaces "mathématiques" ?
En réponse à Régis:
Une surface définie par une équation en coordonnées cartésiennes est de la forme z=f(x,y) où z est l'"altitude" du point en fonction de la position du point (donnée par les coordonnées (x,y)) au dessus duquel il est placé sur le plan de cote z=0. Essaye d'entrer des formules qui ne dépendent que de x, ou que de y, et tu obtiendras la même courbe qu'en 2D mais "étirée": toutes les coupes sont les mêmes.
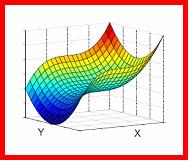
Si tu fixes une coordonnée, par exemple y=2, la fonction x->f(x,2) devient une fonction d'une seule variable, dont tu peux tracer le graphe: c'est la coupe de la surface par le plan d'équation y=2 (tous les points de coordonnées de la forme (x,2,z)). Sur l'exemple ci-dessous, en déplaçant la face rouge avec l'outil tirer/pousser, tu obtiens une coupe dont le graphe est de la forme x^3+constante (puisque y est fixé). De même, en fixant x, tu obtiens une coupe perpendiculaire à la précédente, cette fois-ci de la forme y^2+constante (la classique parabole). Sur l'exemple, il faut déplacer le plan bleu.
Enfin, on peut également représenter les courbes de niveau (comme les lignes de même altitude sur une carte de randonnée, ou les isobares sur les cartes météo), c'est à dire tous les points qui ont la même image par la fonction. Sur un exemple simple de la forme z=f(x,y), il s'agit des points de même "altitude", que l'on obtient en coupant la surface par un plan "horizontal", à z fixé (plan vert sur l'exemple).
J'espère avoir été assez clair, n'hésite pas à demander des exemples concret sinon.
-
RE: Création de surfaces "mathématiques" ?
K-tools, C'est parfait !!!

Merci pour mes étudiants qui bénéficieront de ce support visuel (j'utilisais déjà des logiciels de maths, payants , et ne permettant pas de faire facilement des coupes).
, et ne permettant pas de faire facilement des coupes).
Comment peut-on enlever les grilles, comme sur l'image de la première réponse ? Peut-on également colorer les surfaces ? cela aide encore plus à donner une notion de profondeur, comme sur ces images...
Merci encore !
-
RE: Création de surfaces "mathématiques" ?
Merci pour toutes ces réponses rapides !!
Cela a l'air de répondre totalement à mes attentes, je vous le confirmerai dès que j'aurai eu le temps de m'y plonger en détail...
Pour les aspects théoriques, quel genre d'explication (et de niveau) attendez-vous ? -
Création de surfaces "mathématiques" ?
Bonjour à tous,
je suis enseignant de maths, et certaines fonctionnalités très intuitives de Sketchup m'interessent pour une utilisation en classe. La seule fonctionnalité qui me manque est le tracé de surfaces décrites par une équation cartésienne (genre z=x²+y²). Savez-vous si c'est possible? Peut-être avec la console Ruby (langage que je ne connais pas du tout pour l'instant).
Merci d'avance pour vos réponses !