Création de surfaces "mathématiques" ?
-
Bonjour à tous,
je suis enseignant de maths, et certaines fonctionnalités très intuitives de Sketchup m'interessent pour une utilisation en classe. La seule fonctionnalité qui me manque est le tracé de surfaces décrites par une équation cartésienne (genre z=x²+y²). Savez-vous si c'est possible? Peut-être avec la console Ruby (langage que je ne connais pas du tout pour l'instant).
Merci d'avance pour vos réponses ! -
Si c'est juste pour "l'image finale" d'une forme de courbe
on peut en simuler un grand nombre avec le dessin d'un "chemin" (avec le ruby "Bezier") et ensuite une surface de "profil" que l'outil "Follow me" va propager le long du chemin
-
Oui c'est bien k_tools et j'ai fais un petit essai cela à l'air excellent mais bon il faut maîtriser les formules mathématiques et comme cela fait longtemps c'est pas évident du tout mais pour faire des surfaces courbes ça à l'air efficace.
Si c'est possible d'avoir quelques explications théorique alors je suis preneur.
@+ -
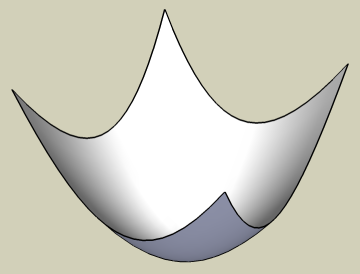
On peut faire les surfaces mathématques si onutilise le script K-tools. Prenez l'option Graphs | 3D-graphs z=f(x,y) puis on peut entrer x2+y2
Bob
-
Merci pour toutes ces réponses rapides !!
Cela a l'air de répondre totalement à mes attentes, je vous le confirmerai dès que j'aurai eu le temps de m'y plonger en détail...
Pour les aspects théoriques, quel genre d'explication (et de niveau) attendez-vous ? -
En fait je ne vois pas comment remplir le champ mathematical formula qui est rempli par défaut avec la formule z=x*y et qui renvoie le résultat qui correspond à l'image que j'ai mis en ligne précédemment donc déjà quelques formules type pour voir comment cela réagit dans un premier temps pourrait me permettre de voir ce qu'il faut inscrire dans le champ de la formule pour obtenir diverses formes.
J'espère être assez clair dans ma demande.
merci d'avance.
@+ -
K-tools, C'est parfait !!!

Merci pour mes étudiants qui bénéficieront de ce support visuel (j'utilisais déjà des logiciels de maths, payants , et ne permettant pas de faire facilement des coupes).
, et ne permettant pas de faire facilement des coupes).
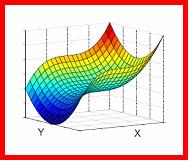
Comment peut-on enlever les grilles, comme sur l'image de la première réponse ? Peut-on également colorer les surfaces ? cela aide encore plus à donner une notion de profondeur, comme sur ces images...
Merci encore !
-
Dommage qu'il n'y ait pas de notice explicative livrée avec k_tool parce que c'est pas du tout évident à maîtriser.
Il ne reste plus qu'à chercher des infos.
@+ -
Il suffit de sélectionner le résultat de faire clic droit éclater ou modifier le groupe et de gommer toutes les arêtes en maintenant la touche alt enfoncée ou d'aller dans la fenêtre adoucir les arêtes et de cocher lisser les normales et adoucir les arêtes.
@+
-
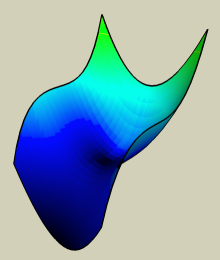
On peut aussi enlever les grilles par utiliser la fenetre 'Soften Edges'. On doit faire 'select all' sur la surface et puis faire click dans la fenetre.
C'est possible de donner une notion de profondeur par utiliser une image comme une texture 'projection'.
Bob
-
En réponse à Régis:
Une surface définie par une équation en coordonnées cartésiennes est de la forme z=f(x,y) où z est l'"altitude" du point en fonction de la position du point (donnée par les coordonnées (x,y)) au dessus duquel il est placé sur le plan de cote z=0. Essaye d'entrer des formules qui ne dépendent que de x, ou que de y, et tu obtiendras la même courbe qu'en 2D mais "étirée": toutes les coupes sont les mêmes.
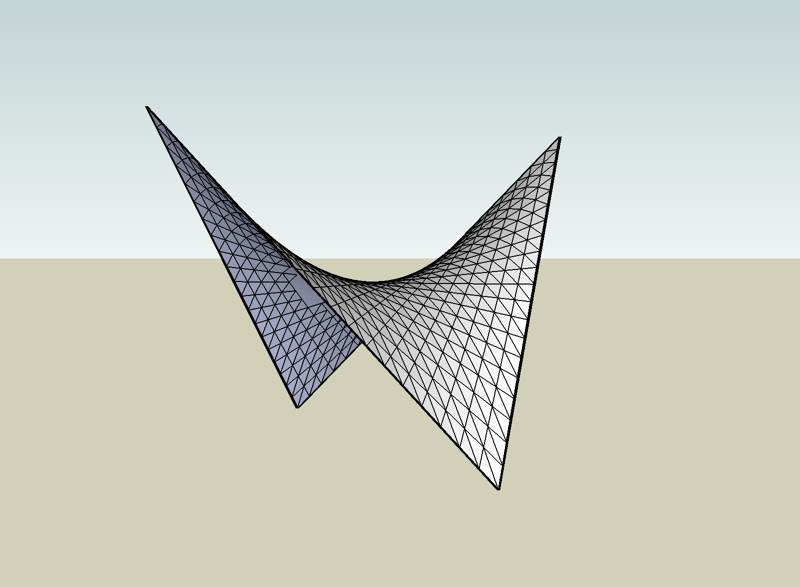
Si tu fixes une coordonnée, par exemple y=2, la fonction x->f(x,2) devient une fonction d'une seule variable, dont tu peux tracer le graphe: c'est la coupe de la surface par le plan d'équation y=2 (tous les points de coordonnées de la forme (x,2,z)). Sur l'exemple ci-dessous, en déplaçant la face rouge avec l'outil tirer/pousser, tu obtiens une coupe dont le graphe est de la forme x^3+constante (puisque y est fixé). De même, en fixant x, tu obtiens une coupe perpendiculaire à la précédente, cette fois-ci de la forme y^2+constante (la classique parabole). Sur l'exemple, il faut déplacer le plan bleu.
Enfin, on peut également représenter les courbes de niveau (comme les lignes de même altitude sur une carte de randonnée, ou les isobares sur les cartes météo), c'est à dire tous les points qui ont la même image par la fonction. Sur un exemple simple de la forme z=f(x,y), il s'agit des points de même "altitude", que l'on obtient en coupant la surface par un plan "horizontal", à z fixé (plan vert sur l'exemple).
J'espère avoir été assez clair, n'hésite pas à demander des exemples concret sinon.
-
Pour avoir des exemples concrets, voici un lien parmi d'autres (il y en a vraiment beaucoup):
http://www.mathcurve.com/surfaces/surfaces.shtml
Bonnes découvertes ! -
Sinon il y a çà Bon c'est pas SU mais...c'est gratuit en tout cas

http://k3dsurf.sourceforge.net/index_fr.html -
J'avais testé kdsurf, mais je ne suis pas parvenu à l'exploiter; il me semble que son but est la représentation d'hyperespaces de dimension supérieure ou égale à 4...
-
@ pischum
Pour l'explication que tu m'as donné plus haut, bon, je vois le principe des différents axes.
Je me suis livré à pas mal de divers test donc j'en ai choisi 3 (alors normalement si tout fonctionne bien, le titre de l'image correspond à la formule que j'ai rentré dans la deuxième boîte de dialogue la première servant à priori à définir les points de départ et les points d'arrivée sur les axes x et y ainsi que la finesse du maillage).
z=(x**2-1)2 - (y2-1)**2
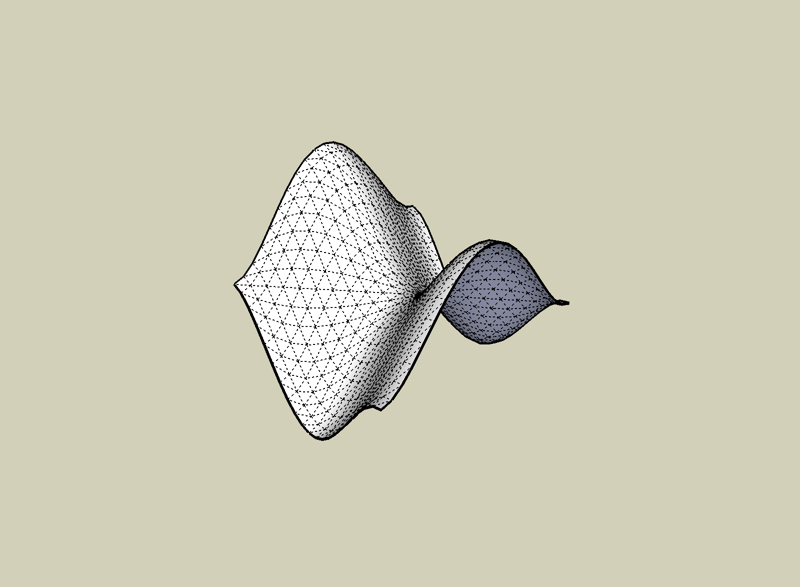
z=(x**2-1)2 + (y2-1)**2

z=(x**2-1)2 * (y2-1)**2
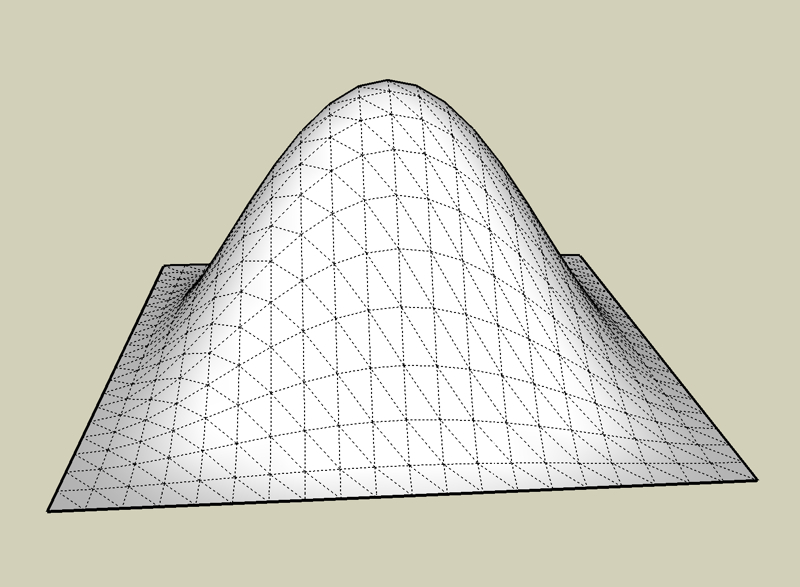
finalement j'ai été obligé de réécrire les formules car il ne me l'acceptait pas comme titre d'image.
J'ai utilisé trois fois la même formule en ne faisant que modifier l'opérateur entre la partie x et la partie y et je dois bien avouer que je sui surpris par le résultat de la troisième image.
Il doit être intéressant de commencer d'abords par les équations 2D pour voir comment cela se goupille et ensuite de les combiner en 3D, en tout cas c'est bien d'avoir un résultat visuel tes étudiants vont sûrement être contents de pouvoir voir le résultat concret d'une équation.
Peut être quelques exemples bien choisis par quelqu'un qui sait pour montrer la mécanique.
Une question: je suppose que ce genre d'équation à ces limites dans ce script ou on peut vraiment faire des choses compliquées avec ?@+
-
With K3DSurf

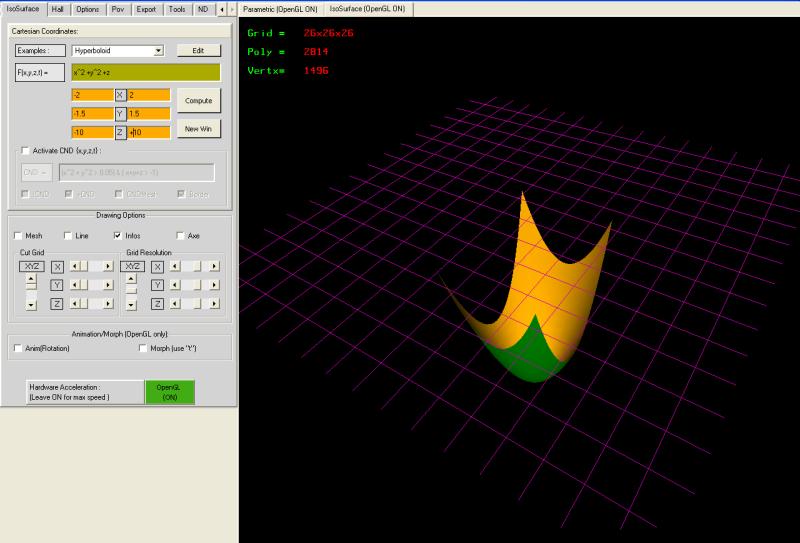
-
@ Pilou: merci pour l'exemple avec K3dsurf, je vais m'y repencher, car j'appréciais bien la manière de se promener au sein de l'image...
@ Régis: les 3 équations que tu mets en exemple n'ont rien à voir entre elles, si ce n'est leur ressemblance dans l'écriture, mais qui ne se traduit pas sur leur comportement "mathématique"; donc leur graphe sont totalement indépendants. Ce n'est donc pas "3 fois la même formule (ou presque)".
Effectivement, pour pouvoir exploiter les coupes des surfaces, il faut d'abord avoir une bonne représentation des graphes d'une fonction d'une variable (genre x^2, x^3, x^4,1/x, sin(x), cos(x), tan(x), etc...).
Quelques petits exercices...
@+
-
@ pischum
pour la première question si je pars du principe que x représente une droite, x2 (x au carré, il me semble que c'est comme cela que ça s'écris en langage ruby) représente une parabole et x3 l'espèce de serpent qui doit avoir un nom mathématique que j' ai oublié depuis une vingtaine d'années au moins alors je réponds que c'est la deuxième image.Et ceux qui est valable pour x est valable pour y.
Pour la deuxième série d'image cela se complique un peu mais je tente
A = 4
B = 5
C = 1
D = 6
E = 3
F = 2Voilà pour les réponses, j'avais déjà fais quelques essais donc certaines formes je les avais déjà faites mais il se peut que je me sois trompé dans mes réponses et comme j'ai passé l'age de tuster j'ai pas tenté les formules proposées.
Maintenant j'ai trouvé des super formules avec des sinus et tout cela fait des trucs terrible mais je ne sais pas du tout comment l'exprimer dans le champ de la formule. Il faut que je fasse quelques tentatives pour voir.Je n'ai pas réellement dit que c'était trois fois la même formule que j'avais utilisé puisque je précise que j'ai changé l'opérateur dans la formule et que justement cela modifie complètement le résultat du graphique et les images le montre bien du reste.
@ pilou
K3d surf à l'air sympa il faudrait que j'essaie pour voir, j'ai vu des images je ne sais plus trop où, d'objets assez suréalistes mais je pense que les formules doivent être beaucoup plus compliquées pour mon piètre savoir mathématique.Dans K_tools il y a aussi (entre autres) la fonction 3d graph spiral. J'ai juste essayé avec la formule qui s'affiche par défaut et cela fait une espèce de coquille de bigorneau mais j'ai pas tenté de l'exploiter plus pour le moment.
@+
-
@unknownuser said:
je pense que les formules doivent être beaucoup plus compliquées pour mon piètre savoir mathématique
Pour le commun des mortels (comme moi) oui, mais comme tout est déjà pré-entré, il suffit de choisir une famille de courbe, la formule s'affiche et de bidouiller les paramètres


Directement dans les cases ou en appuyant sur le bouton Edit
En plus on peut les animer pour voir ce qu'elles ont dans le dos!
-
@ Régis: t'as tout bon !
Advertisement







