CURIOSITE GEOMETRIQUES
-
Faites Glouglou Images pour Jos de Mey
-
Pour ceux qui sont sur Paris, belle expo sur le travail géométrique de Fabien Vienne à la Cité de l'Architecture (au Trocadéro).
Fabien Vienne est un architecte qui a développé des systèmes constructifs autour de la géométrie et les a déclinés en jeux de construction que l'on peut manipuler. À voir et à essayer...Le site de Fabien Vienne
-
Ne pas hésiter à ouvrir ses PDFs! (74)
http://www.fabienvienne.com/pdf.htmlexemple http://www.fabienvienne.com/2/pdf/CIX_port_FV.pdf
Tout à la main, ne connaissait pas l'ordi! S'il est encore vivant, doit se régaler avec les machines d'aujourd'hui!
Pas mal de ses trucs seraient facilement adaptables avec le fumeux Replace Randomly Components by Sdmitch!
-
Pour Chri avec SolveSpace, un petit problème qui devrait être du nanan pour le programme!
http://www.biblio3d.com/t9199-concours-enigme-3d-a-resoudre#108167
(pour la gloire...
Ou toutes autres méthodes, mais un petit gif animé avec Solvespace serait le bienvenu!Hélas comme mon disque dur a fondu je ne peux rien faire pour l'instant!
La figure finale devrait ressembler à cela
(moins la texture oeuf corse!
-
Bonjour
J'ai l'impression qu'on veut pas d'moi
Chri
-
Mince cela dit être encore un truc du genre de nombres de posts minimum!
Ou que tu ne t'aies pas présenté! (cela doit même être cela à tous les coups!
Mets ici tes animations, je transmettrais!
Je te mets le biduleNous avons 4 plans dont les altitudes sont :
- 1200
- 700
- 600
- 0
(cm)
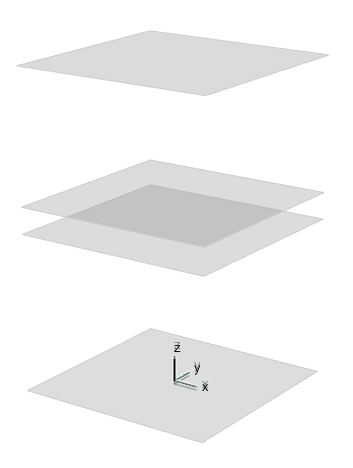
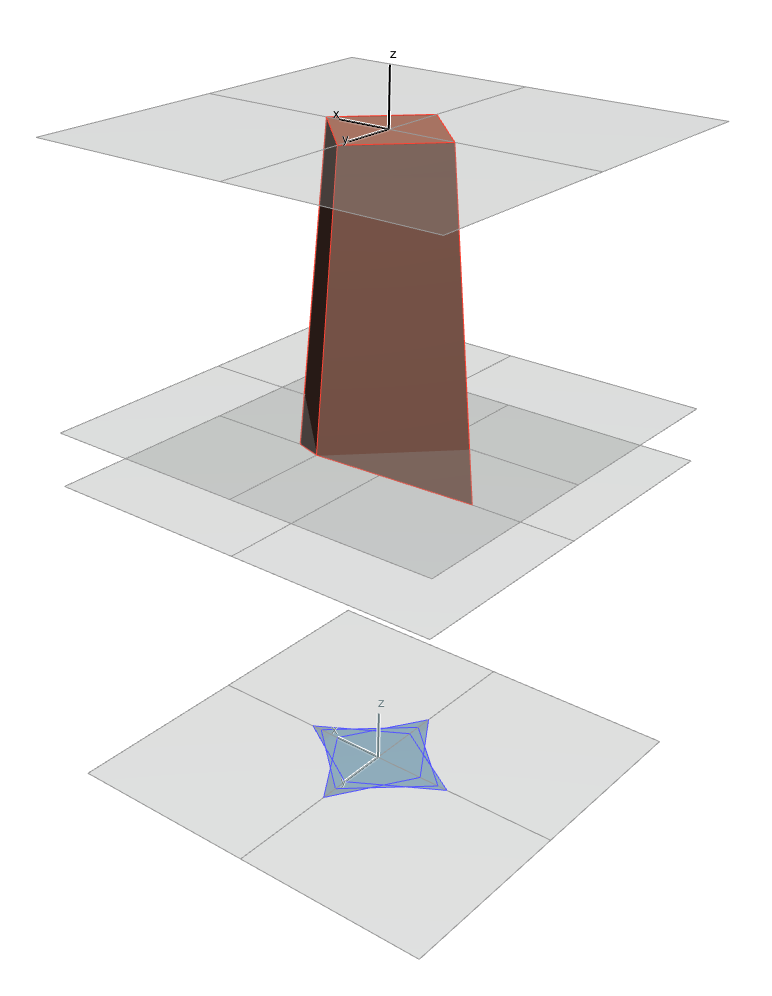
Au centre du plan supérieur, nous avons un carré de 180 de côté.
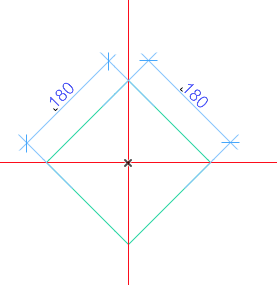
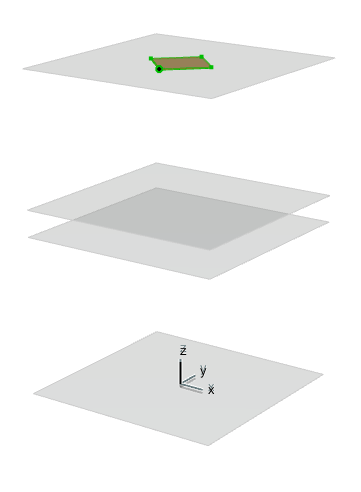
Ce carré est extrudé jusqu’au deuxième plan, et sa base est élargie de manière régulière en suivant la règle suivante :
la distance horizontale entre un coin inférieur et l’intersection entre l’arrête adjacente et le 3ème plan est égale à 260.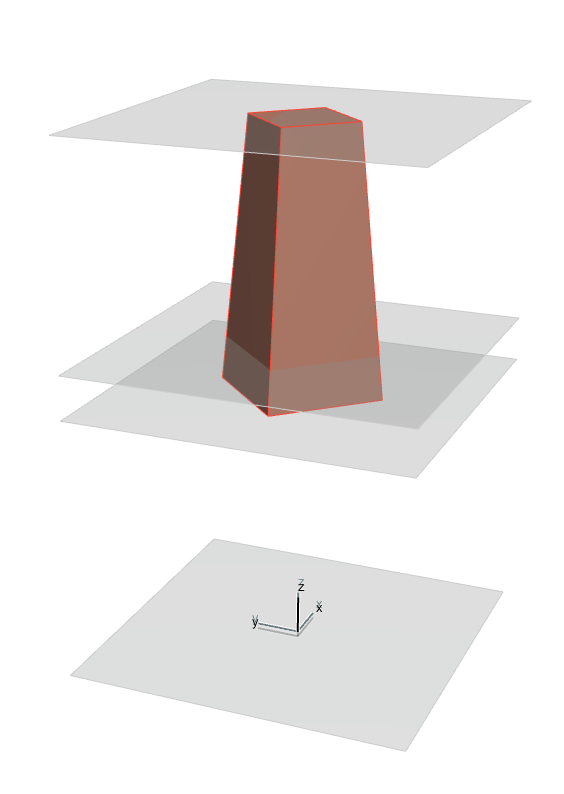
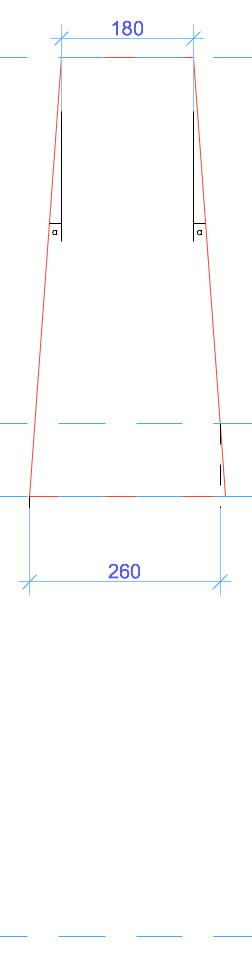
On obtient alors un prisme à base carrée.
Deux coins opposés de la surface inférieure sont remontés le long les arrêtes du prisme jusqu’à l’intersection avec le troisième plan.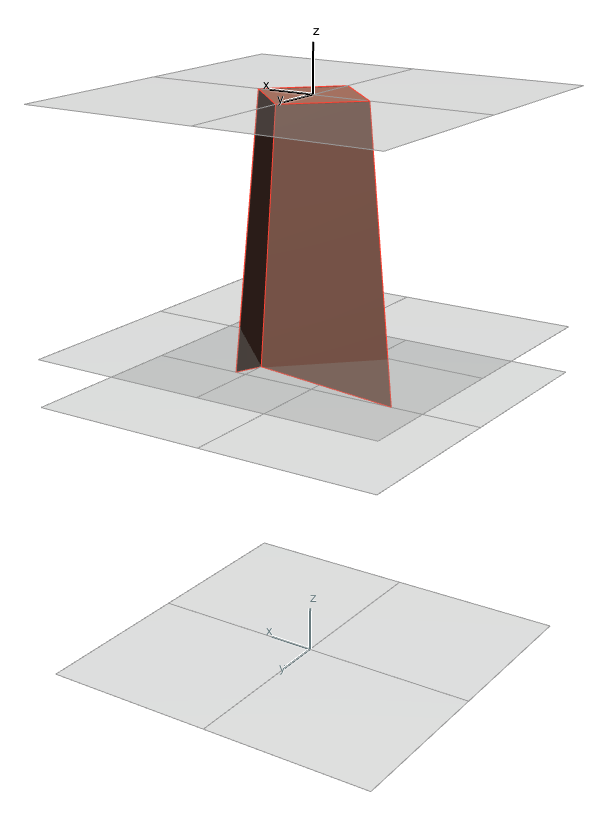
Nous avons donc la partie supérieure de notre solide.
BUT DE l'ENIGME
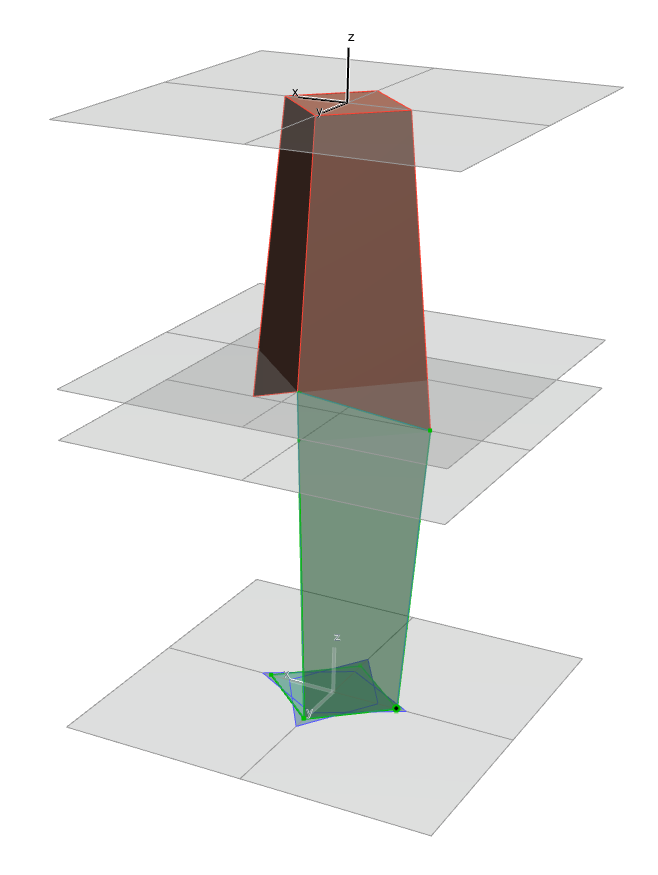
L’énigme consiste à modéliser la partie inférieure de manière précise.
Sur le premier plan, il faut modéliser un losange qui doit respecter 3 contraintes :
- son centre correspond verticalement au centre du carré du 4ème plan
- il mesure 190 de côté
- ses côtés sont respectivement dans les mêmes plans que les arrêtes inférieures du prisme
Vous pouvez donc faire varier les proportions du losange, en faisant attention à ce que les côtés restent à 190.
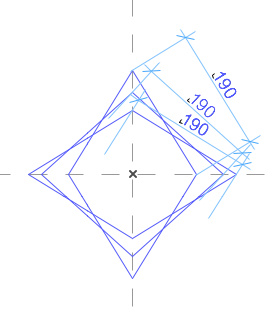
Le prisme supérieur est fixé, non modifiable.
Cette énigme peut être résolue par la géométrie dans l’espace ou par l’algèbre et la trigono. Il est interdit de procéder par tâtonnement incrémenté.
Le résultat final étant :
- soit une démonstration par la géométrie
- soit une fonction mathématique permettant de calculer soit l'angle entre les plans supérieur et inférieur, soit l'une des deux diagonales du losange, en fonction des données connues.
@unknownuser said:
Une construction géométrique sans aucune explication ne suffit pas, il faut un minimum d'explications pour que n'importe qui qui aura suivi tes instructions soit capable de la reproduire. Tu utilises le modeleur de ton choix, du moment que tu postes des images et / ou des explications sur la marche géométrique à suivre.
Le gars dit qu'il a trouvé sa solution
Je suis quasi sûr qu'on peut le faire en direct avec Moi mais j'ai point de machine!
Et qu'en appliquant des contraintes cela doit marcher itou avec SolveSpace!
Bon courage! -
autre possibilité :
GEOGEBRA qui est maintenant en 3Dexemple Section du Cube
https://www.youtube.com/watch?v=oMTfazkkpPAChri
-
Merci, je vais leurs mettre sous la dent pour faire patienter!
Au fait quelles sont les exportations de Geogebra?
On peut récupérer un fichier OBJ par exemple ? -
@pilou said:
Merci, je vais leurs mettre sous la dent pour faire patienter!
Au fait quelles sont les exportations de Geogebra?
On peut récupérer un fichier OBJ par exemple ?Du 3D , je ne crois pas , mais plutôt :
Etape 1
un protocole de construction pas à pas , des lieux définis géométriquement , et donc des cordonnées spatiales en x,y,z pour une recup des coordonnées des points remarquables.Étape 2
Export nuage de points depuis tableur intégréÉtape 3
Construction avec logiciel kivabien à partir du nuage.Faut s'y coller !
Chri
-
C'est moins cool ça!
-
67
-
Bonj
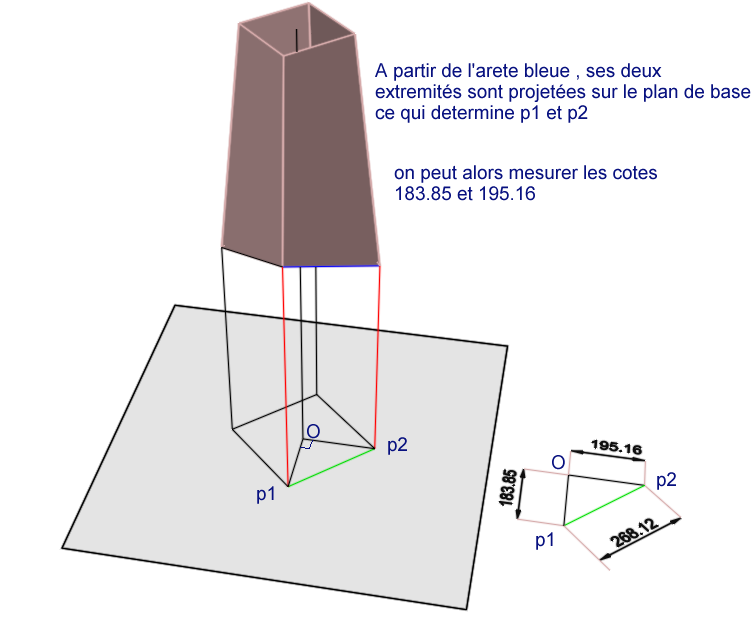
Voici une solution en utilisant Moment Of Inspiration pour modeliser et SOLVESPACE pour determiner les lieux a l'aide de contraintes géometriques.
(haha : en vue de dessus les arête bleues et vertes sont parallèles)
Le fichier MOI a été ensuite sauvegardé en SKETCHUP !
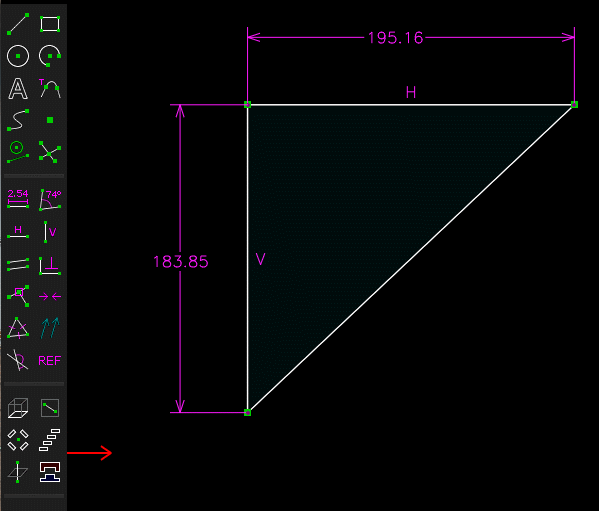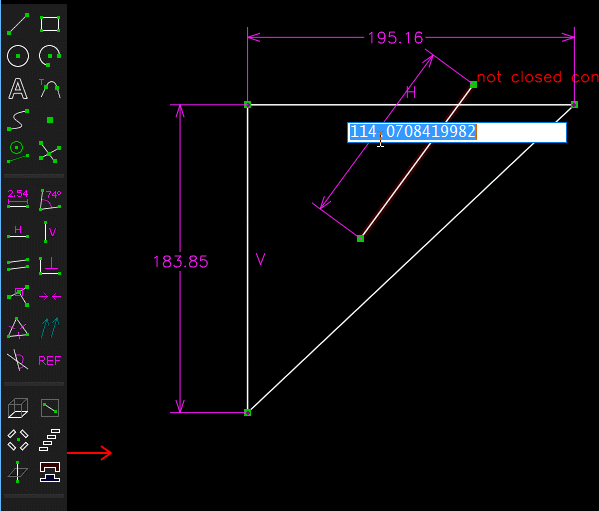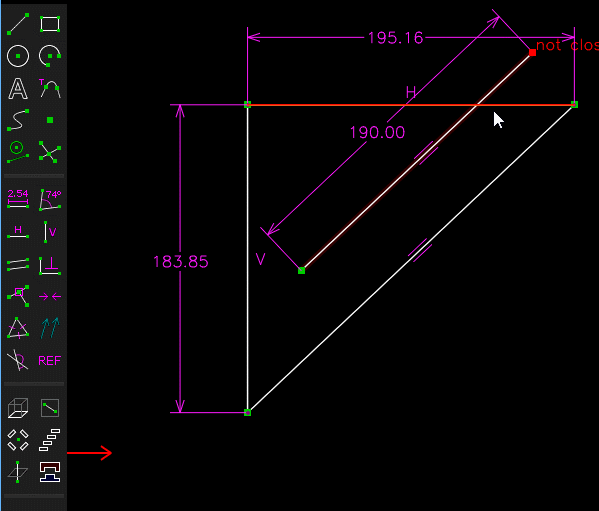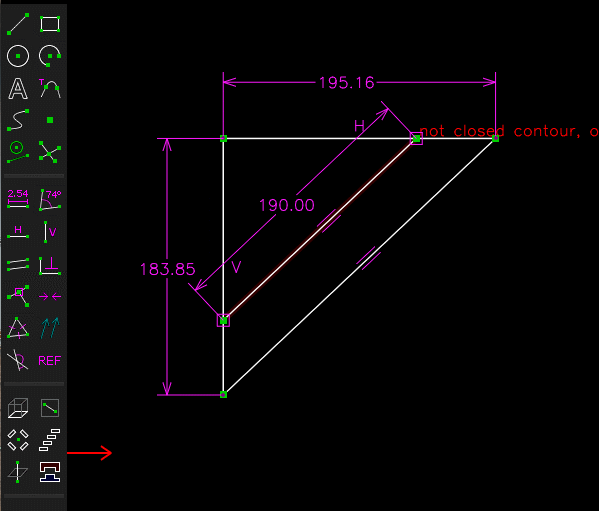
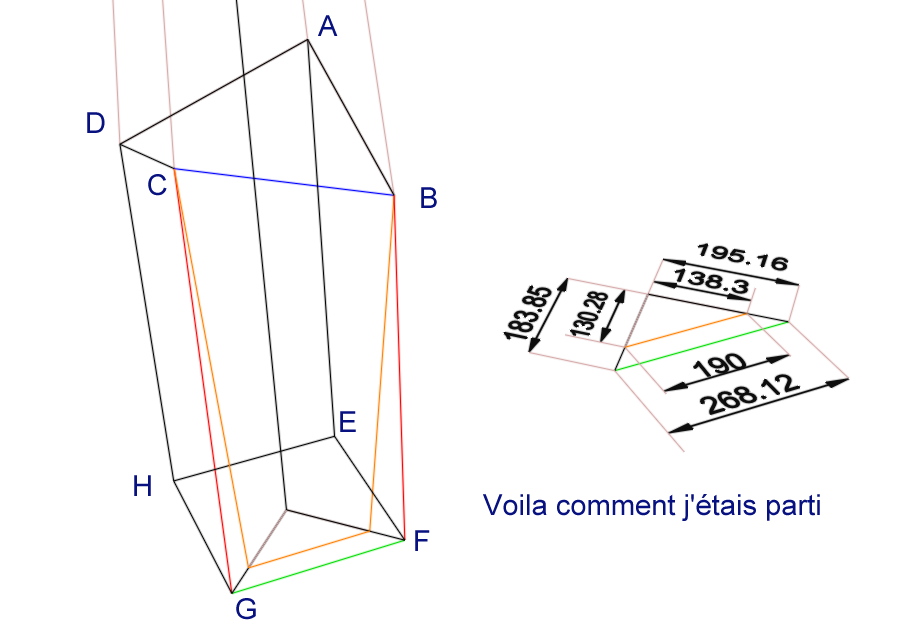
(A partir d'un triangle projeté , un triangle semblable ayant pour hypoténuse 190 mm est determiné , ce qui permet de determiner les cotes 130.28 et 138.30 qui servent a tracer le prisme )
Chri
-
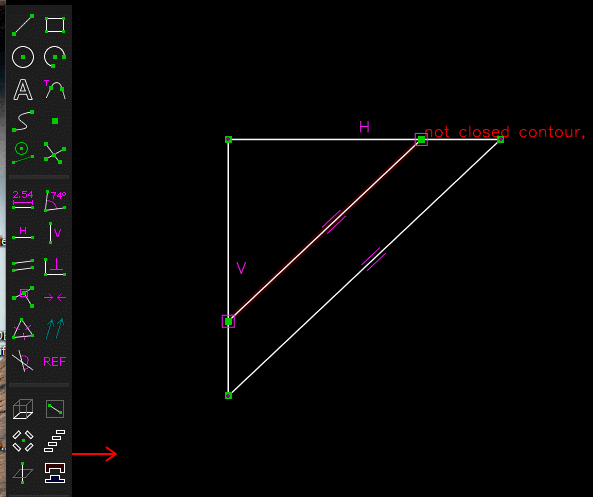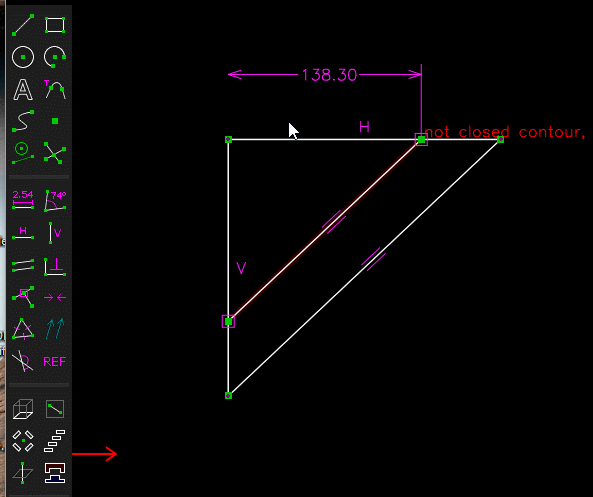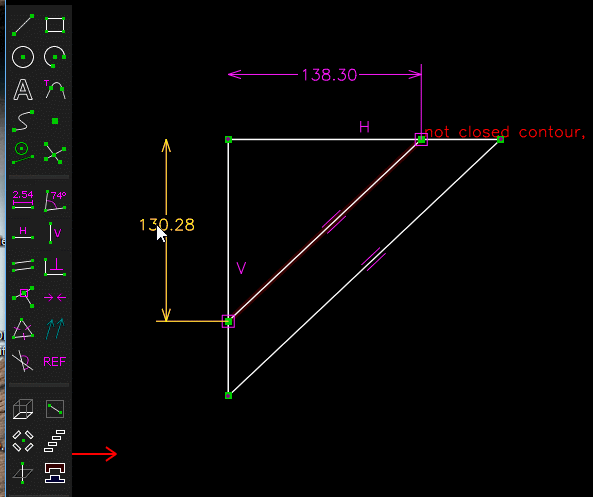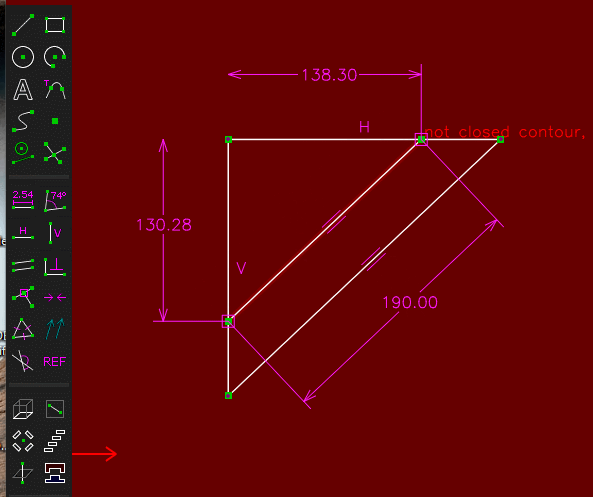
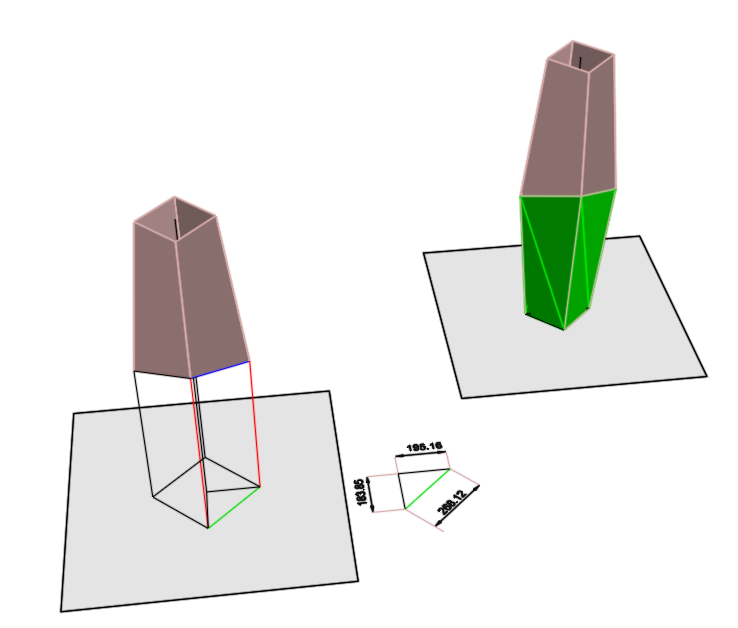
J'ai un doute sur ma manip
Autant je suis sur que les arêtes bleues et vertes sont // , autant la // de la verte sur le plan 0 n'est plus // à la bleue
Chri -
Bon début donc! (dommage que les images aient été chargées sur le forum interne
mais bon je vais trenter de les bricoler avec les matériels dont je dispose!A suivre donc
Pour SolveSpace
Il me semble que j'aurai dessiné une figure du solide d'arrivée complète quelconque
et entré les contraintes au fur et à mesure?Mais bon impossible de faire quoi que ce soit à cause de ce foutu disque dur!
-
Au fait comment as-tu "remonté" les 2 Points ?
-
Il va bien y avoir une connexion au camping des Flots bleus!
-
@pilou said:
Au fait comment as-tu "remonté" les 2 Points ?
Voila comment j'étais [highlight=#ffff80:28u540x4]mal[/highlight:28u540x4]parti !
Sinon , je suis d'accord avec toi , il faudrai le dessiner entierement en parametrique avec SOLVESPACE .
et batir un plan qui pivote autour de BC pour couper les 2 segments du bas en 2 points distants de 190 !Faut juste degager du temps et pas partir en vacances.
Chri
-
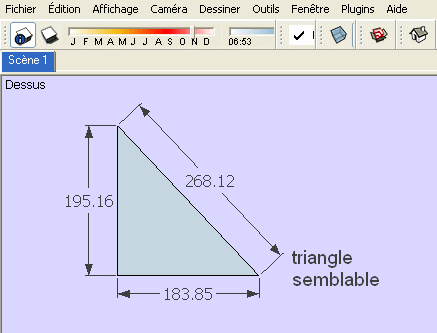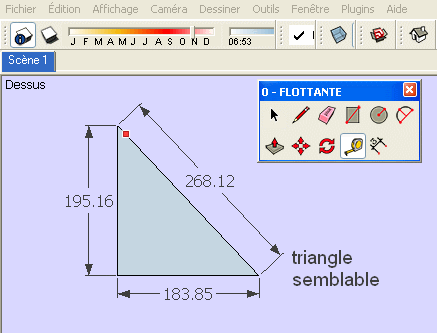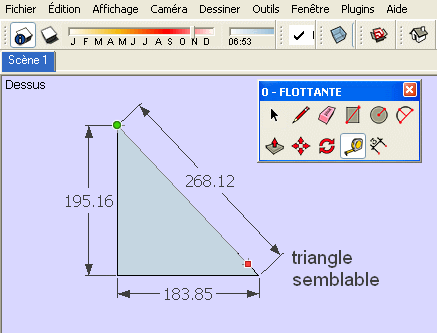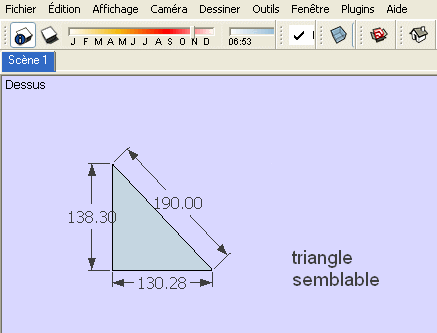
re
plus simplement sans SOLVESPACE puisque l'on souhaite un triangle semblable ( proportionnel)...
des fois , on se mettrai des baffes !
Chri
-
Mon grain de sel
Voici grosso modo mon processus général provisoire! (unité à multiplier par 10)
Il y a une infinité de solutions puisqu'on peut prendre n'importe quel segment qui rejoint le plan 0!!
On prend par exemple le miroir d'une "grande arête oblique" supérieure
on trace un cercle de rayon 19 au bas de celle-ci
Extrusion d'un segment "remonté" le long d'une direction (ici l'oblique)
Intersection du cercle avec cette surface d'extrusion
On obtient le point bas pour le segment de 19Il suffit de faire par exemple une Polyligne dont on a maintenant les 4 points!
Fonction "Plan" pour créer la surface
elle est donc bien "plane" sinon il n'y aurait pas de création de surface!
et on a la surface définitive!
idem pour les 3 autres! En prennant successivement une nouvelle oblique calculée!cela marchera quelque soit la hauteur du plan bas!
(fourniture des 2 diagonales du sujet proposé à suivre)
73,2545031 grande diagonale
64,4405553 petite diagonale de la facetteLe losange du niveau Zéro de 19 de côté a ces diagonales
28,0406855
25,7778086
A vérifier...car j'ai fait à la volée! :
Donc à suivre!
désolé, je ne peux rien sauvegarder pour l'instant!
Les "points chauds" d'intersection ne sont pas tous calculés en direct par le programme pour ne pas ralentir le dessin!
C'est pour cela que certains sont à calculer à part!
-
J'ai refait la construction, il y a un petit problème pour la "partie basse"!
Quand on fait la construction arête par arête, cela ne ferme pas!
Alors que si on fait la construction de deux arêtes successives puis un miroir de ces deux facettes
cela ferme!
Et autre petit tracas: quand on rassemble tout le bazar, cela ne constitue pas un "solide"!
Et ça, c'est pas normal non plus!
A suivre donc!
Advertisement