Using laser distance meters in bright sun
-
Laser distance meters are incredibly useful tools for gathering spatial information when modeling existing buildings and objects. However, I have run into clients and other modelers who haven't used them successfully, so I thought I would share some basic information that might help those who are interested.


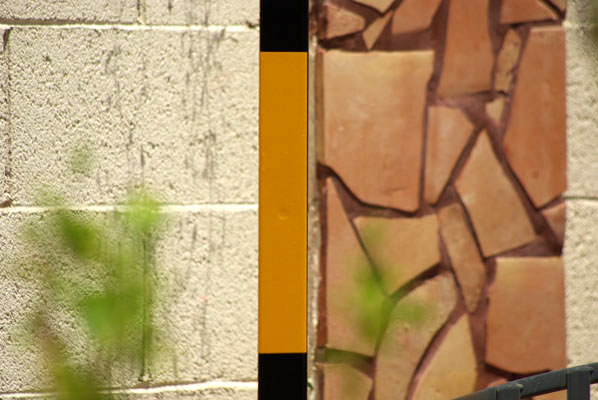


-
False readings. A number of people have told me they get false readings. When I start to probe, I find they are not using a laser distance meter, they are using a sonic distance meter with with a laser targeting device. Sonic meters are OK for gross measurements of a flat wall that is perpendicular to your line of sight and has no obstructions like furniture appliances plants of decorations in your line of sight. The problem is that the sonic column emitted by these devices is an ever widening cone that will eventually be obstructed by some small highly reflective object that will bounce back a signal that is stronger than the bounce from the area you are trying to read. People mistake these for laser distance meters because they use a laser beam to indicate the center of the sonic cone. What they don't realize is that that sonic cone is a thousand times larger than the pencil thin laser and that the laser pointer plays no role in the actual distance measurement. Second, if your target object is not perpendicular to your line of sight the sound will bounce all over the place before returning to your meter. So I pretty much dismiss sonic meters as only being useful in a limited set of circumstances.
-
True laser interferometers are highly accurate in that their accuracy is based on the wavelength of red light at 635 nanometers (trust me that is a very, very, very small distance and highly accurate. My Bosch meter reads to within 1/16 inch of accuracy out to 135ft and Bosch sell even more powerful units. I suspect that the 1/16 inch limit has more to do with instrument cost rather than any limitation of the methodology and perhaps some environmental factors.
-
The problem some people have in working with laser distance meters stems from two factors - working at long distances and lack of contrast in bright sun. Let me emphasize that this is a human perception problem and not a limitation of the instrument itself. The laser meter will almost always return and accurate reading. Even if you can't see the laser dot the instrument can and if the instrument does have a problem, it almost never returns a false reading. It will return an error message instead. The human problem is that if you can't see the red dot you can now exactly what you are pointing at. If you don't know exactly what you are pointing at, you don't know what you are measuring even though the number returned to you is accurate.
-
I have found two solutions to the problem.
a) The first picture above is just there to orient you to a typical working environment in the Arizona sun with 111F temperatures. On the left side of the arbor you will see a black and yellow laser target magnetically attached to the arbor. Now look at pictures 2 and 3 and try to find the laser dot on the brick wall. If you see it in 2 you are crazy because the laser is not on. If you see it in three, you have super powers, but it is there. To help you out drop down to the red picture in the last position. This is the same files as picture three, but I have pumped the hell out of the red channel. It simulates looking through red glasses. See the white dot in the middle of the cinder block? Note the position of the white dot and go back to picture 3. Look in the same position on picture three and you will find a faint pink spot. That pink spot is the laser dot under bright sun. The laser meter sees it well but you don't. -
The first way is to make the red dot easier to see. Look at the laser dot on picture 4. I have moved the dot onto the yellow reflective stripe on my homemade laser target. It is easy to spot in the picture, but in real life the laser dazzle leaves no doubt at all about the location of the place being measured. It is much brighter than your camera and computer screen can show. The dazzle also expands the apparent size of the dot, so both contrast and the effects of distance are immediately overcome. As to the construction and affixing of the optimal laser target that is the subject of an entirely different teaching moment.
-
I call the second approach to targeting your measuring point my "proxy" method or my "faith-based method" because you don't need to see the laser dot. Only the device needs to see the laser dot. By fixing an optical sight on axis or close to on-axis to the laser from the distance meter you can see where the dot should be even if it is invisible to the human eye. You just look through the center of a small monocular and what you see is the measuring point even if you can't see the laser dot. The only problems I have here are ones of cost and manufacturing. For instance, I bought a small monocular for $14 (my budget) over the internet. Leica also offers a $499 instrument (not my budget). The differences between the two instruments? My monocular does not do close focus, it has no anti-reflective coasting on the glass, the glass is filled with microscopic bubbles and little black flakes, and it doesn't have the Leica logo. Still my crude prototype works and I am slowly going through a design process to improve it.
In conclusion, I hope someone finds this info useful and informative. I am working through a long list of issues related to data capture for virtual modeling. Comments are very welcome.
-
-
Thank you Roger.
Your tutorial and practical advice is informative.
I have been watching the Leica brand for several years as an adjunct to data gathering in the field for "as-built" documentation in renovation work. At one time, there was some software made to use with either a PDA or a TabletPC which could be used to transcribe the data into CAD programs. Apex Software, in Texas, also was marketing a version for real estate appraisers that involved a pen enabled TabletPC.
As for Leica, they make a surveying device/system that will generate a point cloud for use in 3d surveying. -
@mitcorb said:
Thank you Roger.
Your tutorial and practical advice is informative.
I have been watching the Leica brand for several years as an adjunct to data gathering in the field for "as-built" documentation in renovation work. At one time, there was some software made to use with either a PDA or a TabletPC which could be used to transcribe the data into CAD programs. Apex Software, in Texas, also was marketing a version for real estate appraisers that involved a pen enabled TabletPC.
As for Leica, they make a surveying device/system that will generate a point cloud for use in 3d surveying.Yes, I asked Santa Claus for a Leica ScanStation C10 with software. But with the software alone going for $16,000 he just laughed. I am more of a guerrilla field expedient type of a guy. Instead of the point cloud I want to hand collect a limited point set I can use to play connect the dots in 3D. Ideally I would like to have a plug in that would read a data set and convert it into C points in 3D space. I could then connect the dots manually.
Sort of looking at the "steam punk" cheapo personal version of the Leica ScanStation. A data collection system for the economically disenfranchised. Tgi3D seems like it has the capability of competing with the lower end of the Scanstation market, but for now I am even one tier below that product at $999.
-
Hi Roger, I agree to all of it. As a landscape designer I do a lot of field work all by myself and since using the Leica Disto D8 all my work goes very easy with this tool. It just shows you a magnified picture on a small screen with crosshairs on the target and you dont nessesarily have to see the laser dot! Also, it calculates the elevation from your position and even transfers the results via bluetooth into your notebook. So you cover 2 of the required 3 dimensions very easy and very precise. Regretably there is no app for iphones as far as I know.
-
I also have a Bosch meter and it has a function to measure the shortest or longest route you are "sweeping through". Here are two, quick sketches what it does:
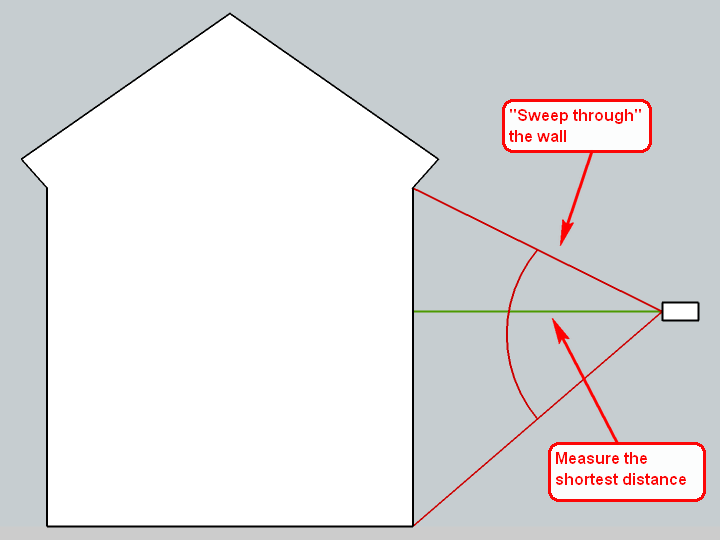
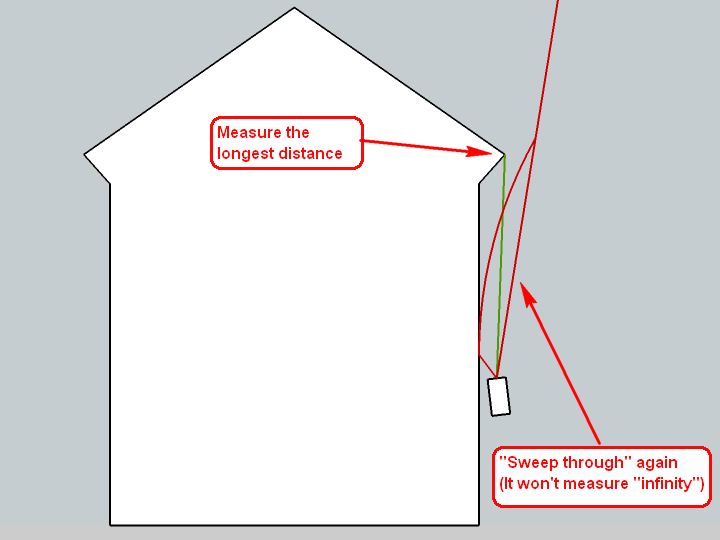
These methods are very handy when I cannot see the small, red dot of the laser scanner (which can indeed happen especially during light daytime on sunny surfaces).I also have a stick of 1.5 metres long which I use to put my scanner on top when measuring the heights of buildings. This way I do not need to lean down to measure from the ground or measure twice (once up and once down from eye/measure height) to add the two values. Basically I start from a footprint, PP it up to 150 cms - then make the measurements and only add what I measure then.
-
Hi, Roger:
I fully appreciate your reply to my reply, especially on the economics. And I was aware that the Scanstation would represent a "significant capital outlay", to use a bland euphemistic phrase.@Gaieus: That method is enlightening. Similarly Leica lets you do a Pythagorean process to arrive at building heights, or other distances. And, as you pointed out, without an established steady station point (top end of stick) the data can be worthless.
-
So what if the walls are not perfectly straight?
Lots of buildings have tapering walls, like Inca buildings, fortresses etc, and many have walls skewed by time/age and bad foundations, like the tower in Pisa etc.
Pythagoras won't help much then, will it?
I'm sure the Leica Disto D8 is a very useful tool, that can also do some angle measurements afaik, but will it be enough power/precision for such situations?
And with a price tag a lot higher (at least in this country ~US$1400) than the tgi3D/PhotoScan I know what I would have chosen But a cheap Bosch laser would probably be quite useful for measuring a reference distance. So far I have gotten enough precision with a 5m tape measure.
But a cheap Bosch laser would probably be quite useful for measuring a reference distance. So far I have gotten enough precision with a 5m tape measure.A bit OT:
A little while ago I saw a TV program from a volcanic rift (?) in Ethopia(?) where the team wanted to make a 3D scan of the extremely hot rift which puffed out toxic gases all the time. They rigged the laser scanner on a steel cable crossing the rift, and lowered it down to make the scan. They had to give up after a while, but they did get some parts of it 3D scanned. I can't help but smiling a little at their efforts, when they could have used the KISS principle and easily/safely gotten good results using PhotoScan (or similar software like PhotoModeler) -
@mitcorb said:
Similarly Leica lets you do a Pythagorean process to arrive at building heights, or other distances.
Yeah, I wished I could get one of those but mine does not do Pythagoras. Of course, I can do it if I really need to

@bjornkn said:
Lots of buildings have tapering walls, like Inca buildings, fortresses etc, and many have walls skewed by time/age and bad foundations, like the tower in Pisa etc.
That's true however the majority of buildings are (fortunately) rectangular/vertical (more or less). If not, we get out our secondary school geometry books again and do some calculations.

-
@gaieus said:
That's true however the majority of buildings are (fortunately) rectangular/vertical (more or less). If not, we get out our secondary school geometry books again and do some calculations.

Wonder how those formulas look?
-
The book are in the attic ATM. I should get them down one day...

-
SOH-CAH-TOA:
Sine = Opposite ÷ Hypotenuse Cosine = Adjacent ÷ Hypotenuse Tangent = Opposite ÷ Adjacentor
Some Old Hippy Caught Another Hippy Trippin' On Acid
-
@gaieus said:
I also have a Bosch meter and it has a function to measure the shortest or longest route you are "sweeping through". Here are two, quick sketches what it does:
DOH! Thanks, I don't remember seeing this in the instruction sheet. But then the whole thing looked so simple that I tossed the instruction without reading. Thanks Gaieus.
-
Well, devices of even the same brand can be very different so there may not be this function on yours. Yet of course looking it up would be best.
-
@Roger :
Afaik sin/cos/tan only works on right-angled triangles, and so do the Pythagoras rule a^2+b^2=c^2 - or here : a=sqr(c^2-b^2)
That's why I was so interested in the formulas in Gaieus' books. Too bad they are in the attic
BTW, did you get that iPhone theodolite to work with any precision?
-
Bjorn, any triangle can be divided into two right triangles, each of which can be solved by pythagoras or sohcahtoa.
-
@roger said:
Bjorn, any triangle can be divided into two right triangles, each of which can be solved by pythagoras or sohcahtoa.
Yes, as long as you know some angles?
Or if you measure from 2 positions? -
While we are on 'formulas'...
If you know two sides of any triangle and the angle between them then you can find the length of the other side opposite that angle using the Cosine Rule
a^2 = b^2 + c^2 - 2bc*cosA
can be rearranged to give the sideathus...
a = sqrt(b^2 + c^2 - 2bc*cosA)
Notes:
Side 'a' is opposite angle 'A'.
There are obviously the other two versions of the equation for the two other sides, but you can give them the reference you want so you always find 'a' without needing to have these in memory!The Sine Rule works for any two angles and one related side, from which you can find the another side
a / sinA = b / sinB = c / sinC = D
which can be rearranged to give the sideathus...
a = b * sinA / sinB
Notes:
Side 'a' is opposite angle 'A' and so on.
The ratios are all equal toD, which is the diameter of the circle that passes through all of the three vertices of the triangle - the radius of that circle isD/2.
To find the area of any triangle where you know two sides and the angle between them use
Area = a * b * sinC / 2
-

My folding meter stick with distance measure on top
Stick unfolded - the distance (outer edge to outer edge) of the two yellow reflective tapes is 3ft.
Laser target bar hung magnetically on wall corner. Reflective tape is 1 ft long and entire black bar is 22 inches.
This is the back of the target bar. The circles are neodymium super magnets affixed with double sided tape. There are also holes in the bar that can be used with push pins, nails, strings, picture hooks, and clamps.
This is the stick with compass
Compass remove and distance meter in place. -
@tig said:
While we are on 'formulas'...
If you know two sides of any triangle and the angle between them then you can find the length of the other side opposite that angle using the Cosine Rule
Exactly!
But you need to know one angle (which may be 90 degrees) and 2 sides to calculate the length of the third, right?
With only 2 sides and no angle you can't know the length of the third side?
But if the wall is vertical (90 degrees) you can calculate without using sin/cos, but just the a^2+b^2=c^2? -
Is there a built-in level in the Bosch laser then?
Advertisement







