Défi - Octaèdre
-
Bonjour Ricco.
Exact, ces Tips & Tricks ou Trucs et Astuces, il y en a pas mal et certains peuvent être d'une grande utilité.
Voir le fichier suivant pour un truc avec les lignes de cotes. Dans ce fichier j'utilise une ligne de cote pour expliquer que les deux objets doivent êtres alignés d'une certain façon. Une ligne de cote me fourni un contenant superbe avec une place pour du texte et deux extrémités féchées pour pointer vers ce que je veux montrer.
Trucs avec les cotes.skp
La scène 1 montre le résultat et la scène 2 montre les explications.Le tour de passe-passe du triple click est moins évident. En effet, avec une cote normale, vous positionnez la fin sur une géométrie avec un click, puis vous tirez la cote de côté et cela génère deux lignes de rappel et la ligne de cote elle-même. Vous complétez avec un dernier click, ça fait donc deux clics pour terminer la cote. Je me suis dit: qu'est-ce qui arrive si je clique deux fois de suite sur le point d'arrivée ? Je devrais ne pas avoir de ligne de rappel et avoir la ligne de cote alignée entre les points de départ et d'arrivée. Et bien non, ça ne fonctionne pas toujours. Avec trois clics, pas de problème. Attention il faut légèrement espacer les clics (environ une demi seconde entre chaque) de façon à aller plus lentement que la vitesse de votre double clic si vous voulez que SU enregistre bel et bien des clics.
Salutations.
-
On va tout savoir
Je vais bien potasser ton truc, j'ai souvent ce pb d'aligner des éléments, " aligner " ne me semble pas simple, j'ai pas eu le courage de potasser tout le mode d'emploi, en fait
Sinon, comment peut on trouver le truc des cotes sans lignes de rappel, c'est écrit où ?
Jamais entendu parler, ou lu ?
Bon, tout ça se bouscule, et pour quelqu'un comme moi qui a le " cerveau lent..."
Car je teste toujours derrière, SU c'est comme la danse, on n'apprend pas que dans la tête mais aussi sur la piste, là, il faut exécuter, dessiner !
A+
Ricco -
Encore à la traine!!
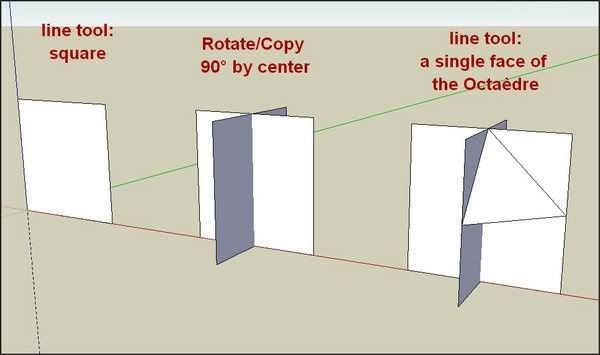
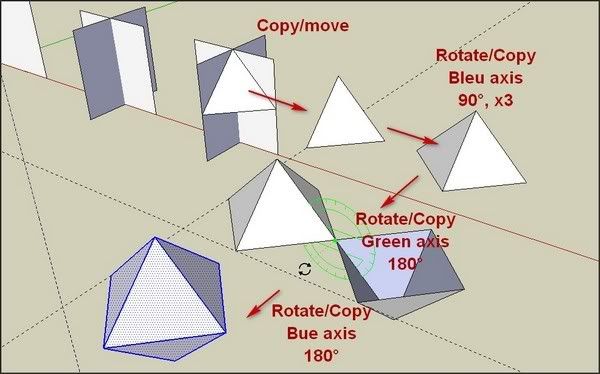
Et je vois bien qu'il y a un défi pyramide que je n'ai pas encore visité.Ma première idée était d'utiliser le FollowMe tool sur un carré. Ca marchait super et j'étais prêt à envoyer le résultat quand j'ai vu que Jean en avait déjà fait son: Octaèdre ultra facile.skp

Obligé de se rabattre sur quelques chose d'un peu moins élégant bon,, Mais enfin je n'utilise que l'outil ligne avec les outils de déplacement et de rotation.
il y a une erreur sur le dernier stade: il s'agit bien sûr d'une simple rotation de 180°

++simon
Ps: on dirait bien que Sergio est un sacré challenger..
-
@jean lemire said:
Bonjour Régis
Ta ligne guide fait 99,992536 au lieu de 100. Mais l'idée est bonne. Il s'agit de trouver une manipulation pour obtenir cette ligne à précisément 100.
Merci et salutations.

Vu,
Même en changeant la précision à 6 décimale, j'arrive pas à être plus précis que trois zéro après la virgule avec cette méthode, je comprends mieux pourquoi SU met un petit symbole qui ressemble à environ devant la cote ~100,0 cm, il considère toujours qu'il y a six décimales même si il n'y a qu'une seule décimale affichée.
Par contre il y a quelque chose qui m'intrigue, racine de 2, il y a plus que 6 chiffres après la virgule, on pourrait presque penser que l'octaèdre n'est pas une forme parfaite, à un moment donné on est obligé de faire une approximation.
@ Pilou
Je te rassure les batisseurs d'aujourd'hui connaissent le principe du théorème de pythagore même si ils ne savent pas forcément comment il s'appelle. maintenant, tous ne l'applique pas rigoureusement, on va au résultat après

@ sergio
Bien vu le coup du demi cercle.
@+
-
@unknownuser said:
Et oui la perfection n'est pas de ce monde
Heureusement, sinon qu'est-ce qu'on s'ennuierait.

-
@unknownuser said:
à un moment donné on est obligé de faire une approximation
Et oui la perfection n'est pas de ce monde

Même les calculs de la machine sont limités
Le malheureux n'a réussi à calculer que 2 700 milliards de décimales de Pi en 103 jours sur son ordi perso!
Le site du fou furieux
-
@lignes de rappel des cotes (Jean

j'ai essayé bien sur et ça fonctionne parfaitement, mais je me demande d'où ça vient, je n'ai vu cette indication nulle part dans la doc, ceci dit j'ai pu passer à côté ?
ricco -
Bonjour Ricco.
Pour le triple clic avec les cotes, effectivement je n'ai vu ça nulle part.
J'ai découvert ce truc à force de jouer avec l'outil "Cotes".
J'ai aussi fait quelques autres trouvailles avec les cotes.
Par exemple, voir le fichier suivant.
Trucs avec les cotes 2.skp
Salutations -
Comme tu dis, tu as bien explorer la question
Je crois que tu avais dit que tu ne connaissais pas Layout 2 ?
me semble t il ?
parce que , ne pas avoir les cotes diamètre et rayon, que leur est il arrivé, c'est assez étonnant quand même
Bon sur la version d'avant il n'y avait carrément pas la cotation, ce qui est encore moins banal pour un logiciel de mise en page.
d'ailleurs dans AutoCad on fait la cotation dans la présentation.
a+ricco
-
Bonjour Ricco.
Les cotes rayon ou diamètre sur Layout ou sur SU ?
Sur SU, je suis certain à 100% que tu connais.
Avec SU, on choisi l'outil Cotes puis on clique sur un objet qu'on n'a pas besoin de sélectionner d'avance. Si c'est un cercle ou un arc, SU propose immédiatement le diamètre. On le pose et ensuite un clic droit sur la cote permet d'en choisir le type: rayon ou diamètre.
Pout Layout, je vais devoir fouiller un peu, effectivement, je ne m'en sers pas pour l'instant.
Salutations.
-
Salut,
je parlais de layout 2 qui a bien évolué, maios vraiment , ne pas avoir ça est étrange, SU, même pas la peine d'y penser, ça le fait tout seul, les paramétrage des flèches, c'est encore autre chose.
Ça n'empêche pas sur Layout de contourner le truc, mais c'est vraiment étrange, faut pas faire de la mécanique avec eux !
Je ne sais pas de quoi se sert Bert pour ses dessins de meubles ?
Ric
Advertisement