Mathematical Formulas to Ruby

[thomthom]

I'm not that comfortable with math containing too many Greek symbols.

But, that's what I'm up against when I'm trying to understand Bézier curves and surfaces.

http://en.wikipedia.org/wiki/B%C3%A9zier_curve

http://en.wikipedia.org/wiki/B%C3%A9zier_surface

What I'm trying to tackle first is Bernstein basis polynomials
http://en.wikipedia.org/wiki/Bernstein_polynomial

I've tried to search to source code that relates to this so I can compare and relate to the functions like that - but without much luck.

For starters:
How would the Bernstein polynomial be interpreted in ruby? (Or pseudo code - whatever)

[remus]

have you had a look at fred06's bezier scripts? i imagine they'll have a lot of this stuff in ruby (and it could save a lot of brain ache for everyone from trying to understand those equations )

[pilou]

Page 125 126
But I believe Fredo6 has made some research about that
He can tell you some tricks

[thomthom]

I looked at fredo's scripts, yes. But the comments are a bit parse - so I don't quite see what is going on.

I've also used the bezier.rb script from Google in a script I'm working one. That's fine and all - but I still don't quite understand what it do. And I don't think the Google bezier uses the Bernstein polynomial.

[thomthom]

@unknownuser said:

Page 125 126
But I believe Fredo6 has made some research about that
He can tell you some tricks

Thanks for that link. I'll look through that PDF over the weekend. Looks to be quite a number of pseudo code examples there.

[fredo6]

@thomthom said:

I looked at fredo's scripts, yes. But the comments are a bit parse - so I don't quite see what is going on.

I've also used the original bezier.rb script from Google in a script I'm working one. That's fine and all - but I still don't quite understand what it do. And I don't think the Google bezier uses the Bernstein polynomial.

Tom,

Actually the code is adapted from the original version by @Last Software. Though I am not specialist in Algebra, I understand what it does. This is coded this way essentially for pratical reasons. The Cubic Bezier were written by Carlos Falé. I wrote the others myself (BSpline, Catmull, etc...) by taking inspiration from existing algorithms.

By the way Bezier curves are based on Bernstein Polylomials (the B(i,n) in your formula). A good application of this is also in FFD.

Fredo

[thomthom]

Is the @Last code using Bernstein Polylomials? I couldn't relate the code to the formula I read. (mind you - I don't know how to read formulas like this.)

[fredo6]

Tom,

Formulas and program algorithms often look different, because the code is usually optimized for iteration rather than direct application of the formula.

Here is an exerpt of the Wikipedia notice.

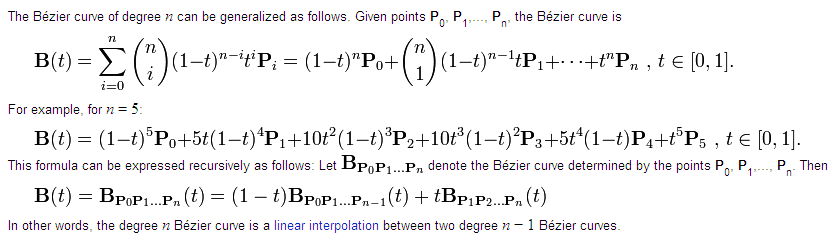
The notation in parenthesis Cn,i are simply binomial coefficients given by the formula

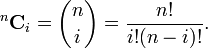
t is simply the parametric variable, between 0 and 1 to tell where you wish to interpolate the value of the Bezier curve (when you ask for a precision of 20 segments, then basically t is taken from 0 to 1 by increment of dt = 1/(20+1).

def BZ__BezierClassic.evaluate(pts, t)

    degree = pts.length - 1
    if degree < 1
        return nil
    end
    
    t1 = 1.0 - t
    fact = 1.0
    n_choose_i = 1

    x = pts[0].x * t1
    y = pts[0].y * t1
    z = pts[0].z * t1
    
    for i in 1...degree
        fact = fact*t
        n_choose_i = n_choose_i*(degree-i+1)/i
        fn = fact * n_choose_i
        x = (x + fn*pts[i].x) * t1
        y = (y + fn*pts[i].y) * t1
        z = (z + fn*pts[i].z) * t1
    end

    x = x + fact*t*pts[degree].x
    y = y + fact*t*pts[degree].y
    z = z + fact*t*pts[degree].z

    Geom;;Point3d.new(x, y, z)
    
end

Then for each t, you compute the value of the coordinates (x, y, z) of the curve point, based on the control points pts.
The code is simply computing the same polynomial formula above in a loop on the degree (number of control points - 1), by summing the value of coefficients with the ones calculated at the previous step of the loop.

You recognize fact, which actually will hold the factorial for the degree variable and t1 which is simply (1 - t).

The rest is simply a matter of arithmetic.

I agree this is convoluted, and this is why, the best is to get inspiration of existing algorithms written in whatever language, to convert them to Ruby and then possibly improve them (the one used by @Last seems to be orginally written in Fortran).

So, to your question: YES, Bezier uses Bernstein polynomials (based on factorials)

Fredo

PS: Rereading the code, it gives me the idea to improve it a bit for Ruby.

[thomthom]

Thanks Fredo.
I've taken an interests into Bèzier patches. And while I could easily produce a patch using the @Last bezier.rb, I wanted to try to understand more about how it worked technically.

That way I could eventually improve the method I use to create the patch, as at the moment I'm not sure if it's efficient the way I do it.

But yea, Bèzier curves are really cool. Thanks for your feedback Fredo.