[Tutorial > Modeling] truncated icosahedron revisited
-
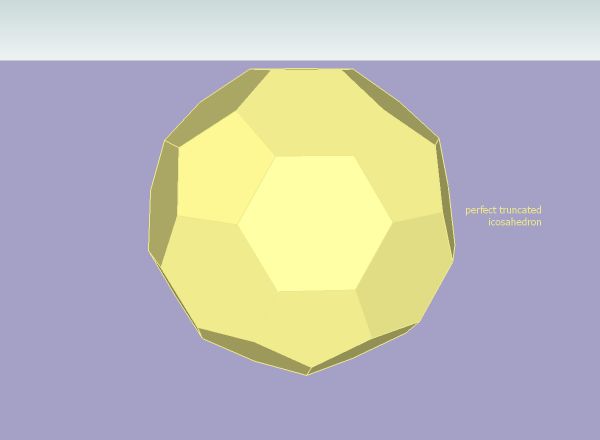
Here's a way to build a truncated icosa from scratch. I'm sure there are other ways! The secret here is to assign a lot of points to the construction circles so that a "true" intersection can be calculated.
-
caddict,
I had SO many problems with the same thing last year. There was a discussion on one of the Google groups regarding the truncated icosahedron, face-rotations and intersection accuracy. This generated a lot of experimenting with face rotations, and several new discussions.
Everyone agreed that SketchUp could use some kind of enhancement to the rotation tool that would allow inferencing to a precise intersection point on a line. Who knows if we'll ever see it. The concensus was that everyone would love to be able to rotate two faces up to their intersection point (line, actually.)
I'm afraid that I sorta 'killed' the discussion about the truncated icosahedron (the original topic) with an historical construction method:
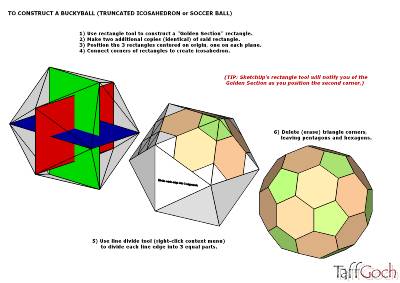 http://sketchup.google.com/3dwarehouse/details?mid=3af9af9384d2097858f8f3aa29de1c06
http://sketchup.google.com/3dwarehouse/details?mid=3af9af9384d2097858f8f3aa29de1c06However, the rotation issue still hasn't revealed any 'eureka' moments, where someone has provided a workaround. It's been discussed before, but maybe this time someone with a fresh perspective will surprise us all. (I've got my fingers crossed...)
Regards,
Taff -
Thanks Taff, your constuction method is great...I didn't know about the golden section relationship. I wish I'd come across that discussion earlier!
The method that I have submitted does generate a perfect regular shape (within the rounding off limits of SU of course...does anyone know what that is?)
The key is drawing two construction "circles" and rotating two adjacent hex faces until their vertices snap on to the intersection point of the circles. Once this point is located, the rest of the polyhedron can be constructed.
It only works if the "circles" are assigned a lot of points. I used 1000 which means each circle is really a polygon with 999 edges. Then when they intersect, a point is generated which is close enough to the true intersection point to allow a perfect solid to be built.
I guess this method could be used in other mathematical constructions requiring intersections of circles.
-
caddict,
Using 1000 edges for the circles provides pretty good precision. If you go into 'Model Info > units' and change the precision to it's maximum (or is it 'minimum',) the 'entity info' box shows that the rotation has reduced the hexagon edges from 1000mm, to 999.997867mm.
Certainly, in real world construction, 0.002mm precision is more-than-acceptable. It's highly unlikely that this degree of precision would ever be necessary or practical.
But for mathematically-obsessive personalities, like me, I still want to know why SketchUp doesn't provide the capability to rotate/intersect precisely. Computationally, it's possible - but SketchUp doesn't implement such an inference.
Regarding your method, if you use the 'Model info > units' settings to set an even higher precision, and you play with the 'snapping' setting, I suspect you can achieve even greater accuracy.
Since the entire circle is not needed, you could draw just the arc portion of necessity. If you set the arc segments to 1000, as you did for the circle, you might approach an exact 1000mm hexagonal edge.
Another trick is to scale the entire model up, perform the rotations, then scale back down. Since SketchUp is sensitive to small dimensions, and can thereby 'choke' on certain operations, the up-scaling circumvents the problem. You could scale up by a 100x-1000x multiplier, if necessary.
If you're trying to produce a soccer ball, this degree of precision borders on ridiculous. But what if you're trying to model a soccer ball for nanobots to play with...?

Regards,
Taff -
Cool constructions!

Do you know TopMod?
-
Pilou,
TopMod looks fun - and it's free? So, what's the catch?
I see that it's from the university, Texas A&M. Perhaps free distribution simply increases the exposure and reputation of the university's computer-visualization program, thereby ensuring greater student enrollment.
In your opinion, how good is the program?
Taff
-
It's not good, it's excellent!

It's free of course!
A topologic modeler!
With it you can make some crazy geometric structures very easily, impossible in a twinkling with other 3D programs
Some of these are made with it!
You can export the result in OBJ format (so transform it in 3DS for importation in SU)
(you can use a free another one for converter format obj--> 3ds like anim8Or or Blender or any you want
see the gallery
Don't make texturing with it just the modelize!And nothing to inhibit to modify the result in another 3D prog

-
Topmod does look very interesting will definitely look into it.
Taff, there are a lot of interesting things here. Like when does SU decide that two points are close enough to become one point?
And about precision. Plato and Archimedes contemplated these perfect geometries. I think they might be disappointed that even now with all our technology, even in the virtual world of computer graphics, the only place a perfect shape exists is in still in our minds!
I would guess that even with the best possible software the position of any point is just an approximation to some pre-assigned level of precision.
I don't know how SU works...presumably a circle is represented within the program by its equation. Then the intersection of two circles is found by solving their equations simultaneously. AFAIK all programs use methods of successive approximation to solve equations. Which means that the point which is calculated is only an approximation! And when it comes to representing these things on a screen, the pixel is the limit. So those nanobots may have to wait before they can get perfectly shaped soccer balls!
Enough philosophy. I tried the same construction in another application...Moi, which btw is brilliant, but quite different from SU. And the precision issue didn't even come up. It just found those circle intersections straight off and rotated those hexagons exactly to the point without any doubt. One of the things I love about 3D work is that all applications are different and have different ways of doing the same job
Cheers,
Steve
-
Here is another bit of fun that you might enjoy. I thought that if the icosahedron was truncated, what is the object that is truncating it?
-
So now you can take a look to 3KDSurf

(free of course
-
Thanks Pilou

You are a source of great software! This one looks so good. Never before has there been so much free stuff!
Also I think your artwork is really great and unique I would say
I have just had a look at K3DSurf. It is really good. It is beautiful that such amazing shapes can be generated by mathematical functions!

-
It's a pleasure!

So for the fun : a good habitude beginning the day with 5 minutes of fun

Chaoscope
The more easy true gem!
Choose family (and view gaz for exploration) then Only 3 keys!
F3 = explore (then move rotate size with the mouse)
F4 = Calculate render
ESC = Stop
Have fun discovery!
My speedies of the day
Free of course


-
As a newbie, I was going to ask about the best way to model a carbon nanotube (think hexagon lattice rolled into a tube) but these links to TopMod and 3KDSurf are going to keep me pretty busy! Many thanks for the links.
-
Hey Pilou I can't believe chaoscope

The possibilities for beatiful pictures are endless!And Simon, about the nanotube. I think it is worthy of a new topic! See Tutorials

-
Advertisement








