Medeek Engineering
-
Version 0.8.4 - 11.21.2025
- Fixed a bug with partial bearing at end supports.
- Added the bearing area factor (Cb) to the bearing calculations and adjustment factors table.
- Added the "Braced at Supports" option to the top and bottom lateral bracing options.
- Fixed the lateral bracing algorithm for bending so that blocking at supports is enabled (bracing at top and bottom).
- Fixed the algorithm for lateral bracing so that the unbraced length is correctly calculated.
-
Tutorial 2 - Lateral Stability (18:31 min.)
-
The other issue I am a bit unclear on is the unbraced length (lu) especially in the case of checking negative moments in multi-span situations (unbraced bottom). I've checked a number of examples in Donald Breyer's book "Design of Wood Structures". Rather than considering the lu as the actual span he is calculating the lu as the distance between the points of zero moment. I could use a bit of clarification on this. Section 3.3.3.4 of the NDS (page 17) only talks about the distance between points of intermediate lateral support.
After giving this some more thought and digging through the NDS a bit more I think the reason that Breyer makes this assumption is that the language in the NDS for computing the Cv (volume factor) does say the distance between points of zero moments. He then seems to extends this idea to computing the CL by using the same logic to determine the unbraced length (on both sides of a support). See example 6.28 in chapter 6.16.
My only problem with this is that it would seem like it would be unconservative in many cases with multi-span beams where you are computing the CL for negative moments (at supports). However by using the full intermediate span length as the unbraced length perhaps it is too conservative. I wish the NDS would give more guidance on this matter, I can only guess at the intent and supposed correct algorithm at this point.
Let's consider the example shown in the image below:
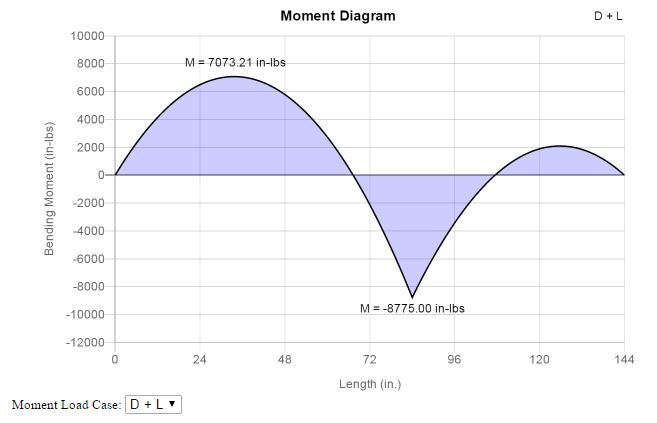
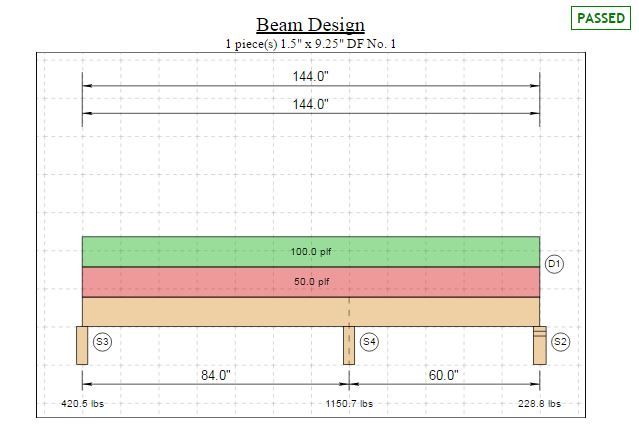
If we consider that there is no lateral bracing at the intermediate support at 84" (bottom of beam) then per Breyer's method the unbraced length is between points of zero moment (x=67" to x=108"), so the unbraced length for the negative bending (neg. moment) is equal to 41". However I would argue that it is the full beam length, both spans, so 144".
If we do consider that the beam is laterally braced (bottom of the beam) at the intermediate support at x = 84" then Breyer considers the worse case of the two conditions 84 - 67 = 17" and 108 - 84 = 24" and he concludes that the unbraced length should be 24". I would look at both spans on each side of the support or max. negative moment and take the larger of the two 84" > 60", so the unbraced length should be 84".
Thoughts? Am I too conservative?
On a slightly different note I would use 41" length to compute my Cv for the negative bending (for both cases given above). This is per the NDS verbage (Sec. 5.3.6).

-
Version 0.8.5 - 12.05.2025
- Updated the licensing system with an improved algorithm (bug fix for SU 2022 and greater).
- Added a "Deflection Analysis" tool to the main toolbar.
- Added deflection analysis as an option within the beam context menu.
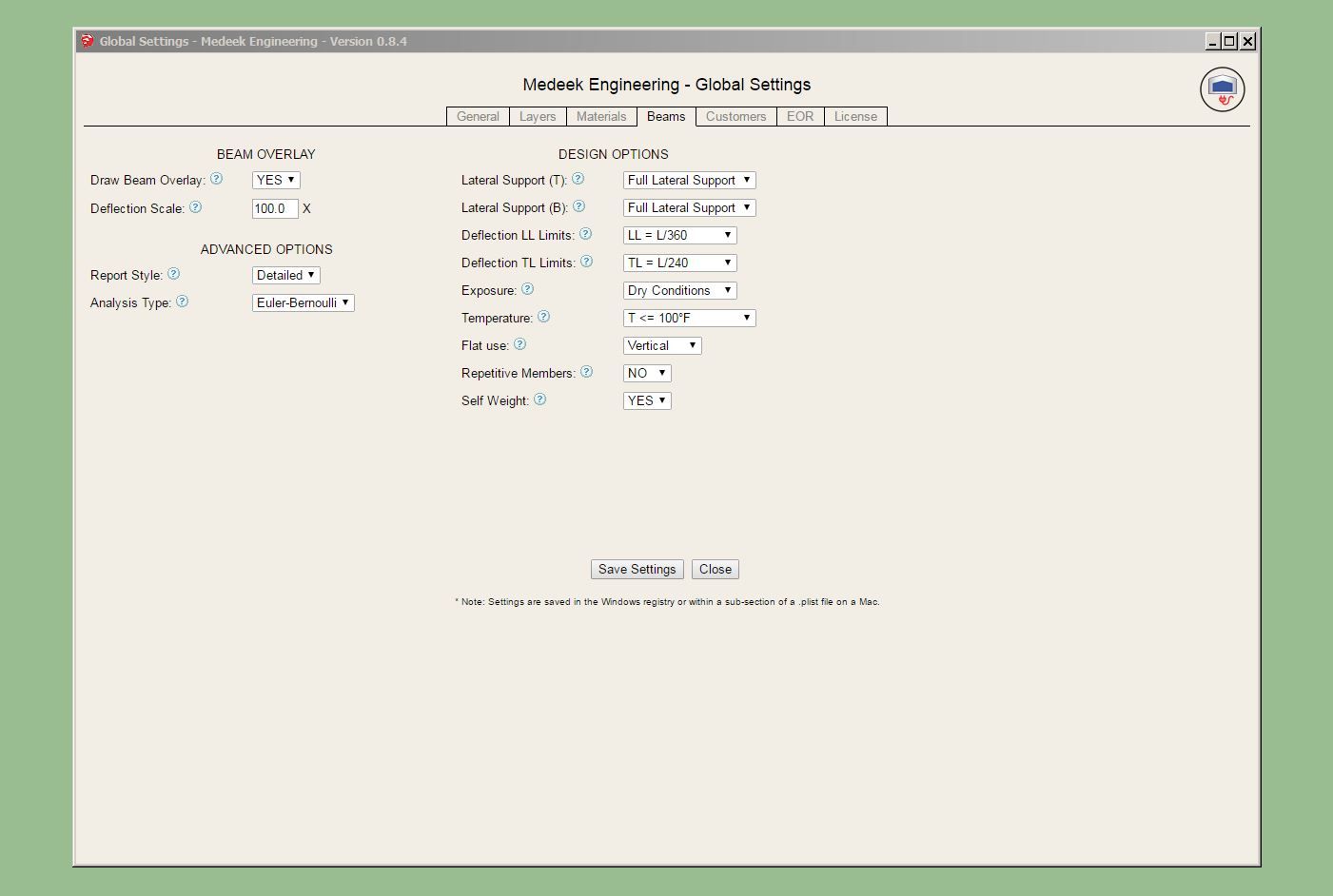
- Updated the "Beams" tab of the Global Settings with various options.
-
just in case you needed another rabbit hole... https://www.apawood.org/ftao
-
After the Beam calculator I need to put together the post/column calculator, then the footing calculator, then the shear wall calculator and then maybe the FTAO shearwall calculator.
Advertisement








