CURIOSITE GEOMETRIQUES
-
Tiens j'ai (re)trouvé ça!

Un tuto VF sur OpenSCAD
http://www.openscad.org ou le langage 3D (gratuit)
(gratuit)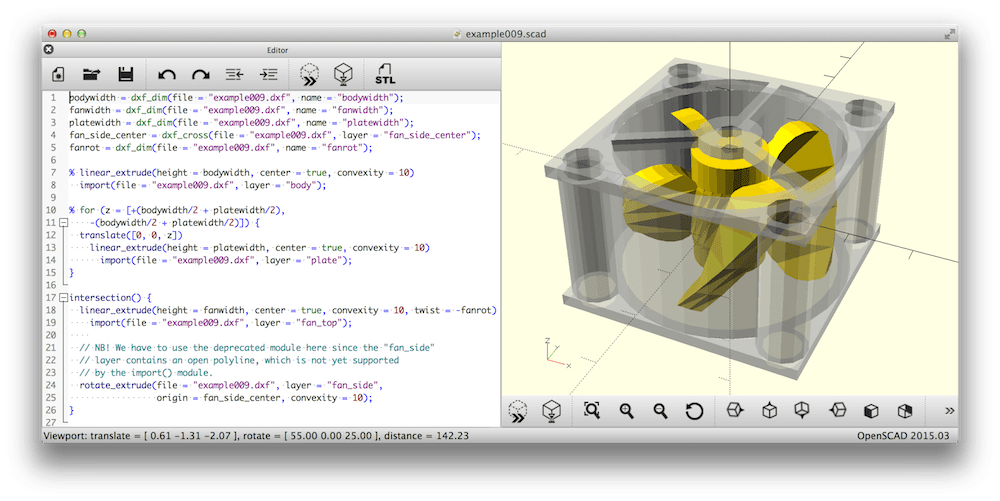
-
En fait cela va plus vite de prendre le plus court, on peut utiliser du coup la fonction
Etend !
M'enfin bon, Le bon Moi daigne se caler sur une valeur de 10 sans décimale
sur ces valeurs-ci!
(toujours pas trouvé de construction gémétrique simple)
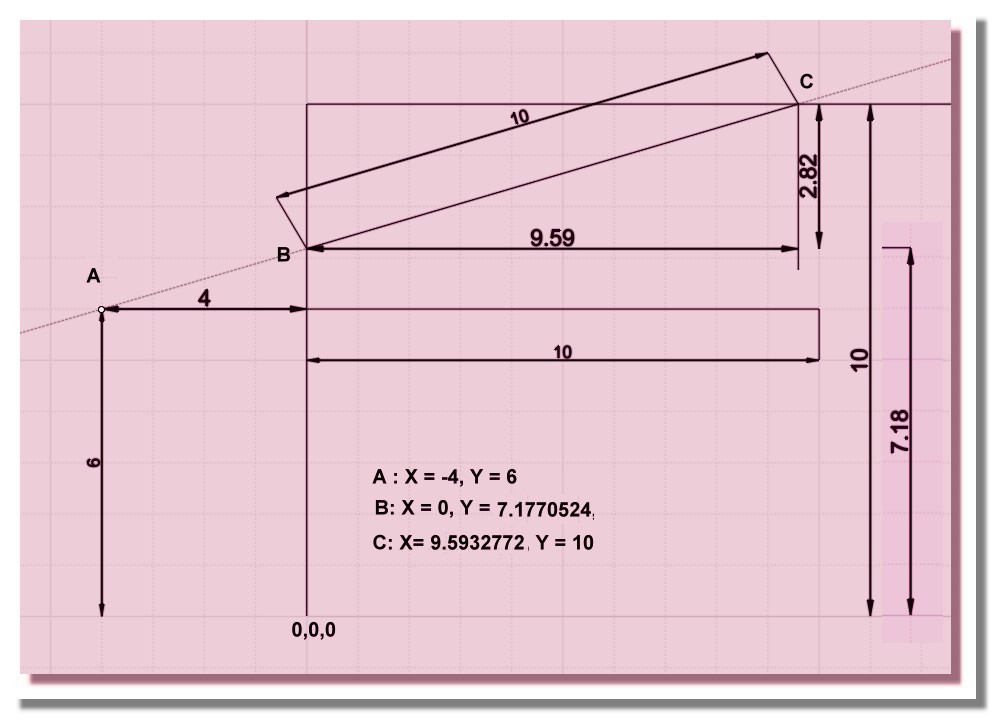
Ce qui ne donne quand on applique ce petit théorème Pythagoricien!

9.5932772 puissance 2 + 2.8229476 puissance 2
100.0000005883856! On peut pas dire que ce soit exactement 100!
PS Bizarre ça, je croyais que les dimensions dans Moi acceptaient le nb de décimales des options! ?

Ci-joint le 3DM!
-
Bonj
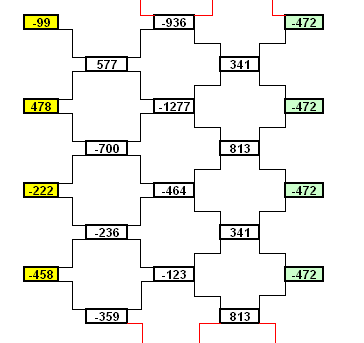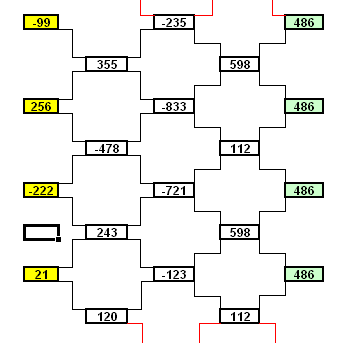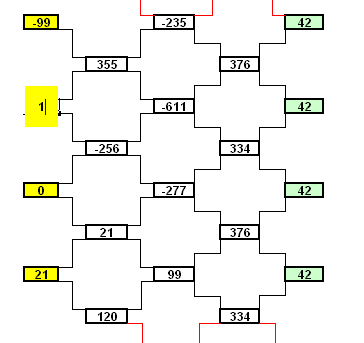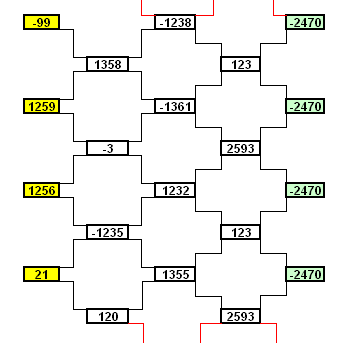
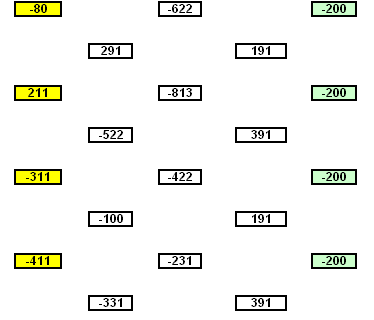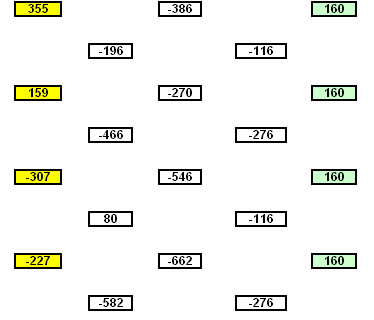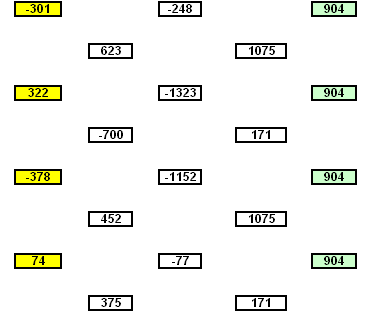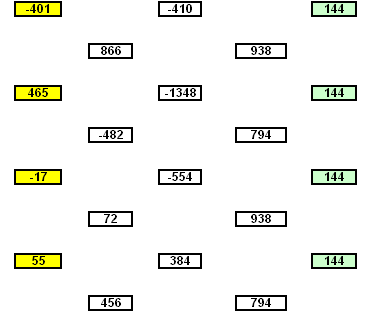
Trouvez ci-joint une curiosité numérique . ( CERCLE DE DUCCI )
Si cela vous tente , vous pouvez en essayer une représentation.
J'ai trouvé cela ici : http://villemin.gerard.free.fr/Wwwgvmm/Iteration/CercDucci.htmDESCRIPTION :
Dans un tableur , quelque soit la valeur des 4 cellules de départ ( en jaune ) , en posant qu'un nombre est la différence de ses 2 nombres de gauche , la valeur des 4 cellules vertes , a droite sera toujours identique.
... et je ne sais pas pourquoi !
ETONNANT , NON !Chri
-
Parce que!
 La recherche sur Internet évite de se cramer trop longtemps les neurones!
La recherche sur Internet évite de se cramer trop longtemps les neurones! 
Ce qui est pas banal c'est que cela marche quelque soit la longueur des nombres!
J'ai quelques doutes...
Comme ce contre-exemple le montre!
3 ,123, 5555, 10
..120, 5432, 5545, 7
... 5312, 113, 5538, 113
......5199, 5425, 5425, 5199
..........226,0,226,0 Humhumhum
Bon, j'ai fait ça avec un crayon et du papier à vérifier donc..@unknownuser said:
La démonstration passe par les étapes suivantes:
-
Démontrer que le plus grand nombre décroît en, au plus, 4 tours: si 10 est le plus grand nombre, il faudra, au plus, 4 x 10 = 40 tours pour atteindre 0. -
S'il n'y a pas de 0 au départ, la décroissance est assez évidente. -
Dans la mesure où le plus grand atteint 0, les trois autres sont aussi à 0. -
Et, avant d'arriver à 0 tous les quatre, ils sont tous égaux. -
Pour démontrer la décroissance vers 0, il faut considérer la présence de 1 à 3 zéros à côté du nombre le plus grand. -
Avec 3 zéros, ils disparaissent en 3 étapes. -
Avec 2 zéros, on examine les sous-cas: ils sont adjacents ou opposés. -
Avec 1 zéro, on considère les trois autres nombres; s'ils sont tous différents ou non. -
Un peu laborieux, mais de la pure scrutation des cas possibles. Plus facile à voir avec les dessins.
-
-
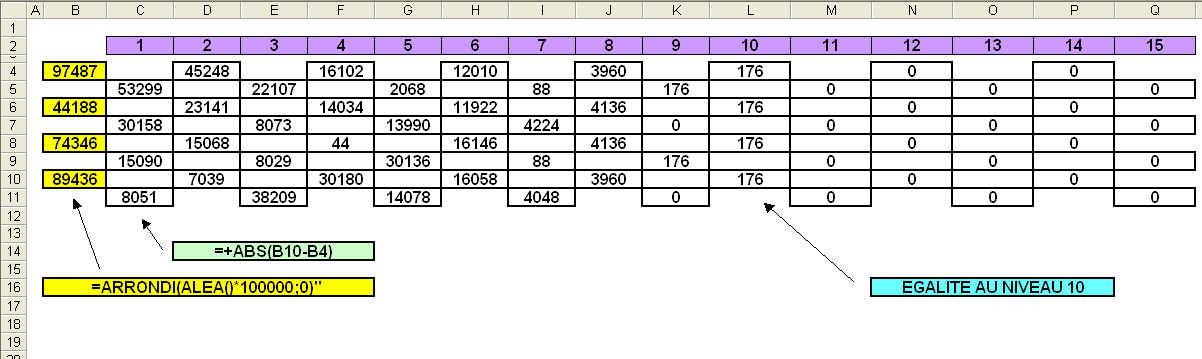
Bonjour PILOU
Pour info , voici le mode de calcul correspondant a mon tableur:
Je l'ai fait avec tes valeurs de départ .
( Tu remarqueras dans mon calcul des nombres négatifs )Mon calcul , a l'air de fonctionner dans toute les config
Trouves ci-joint , en Zip , un EXCEL que j'ai bricolé avec un generateur de valeurs de depart aléatoires ( recalcul par F9 )
Je tenterai bien une représentation graphique ... mais laquelle ?
Chri
-
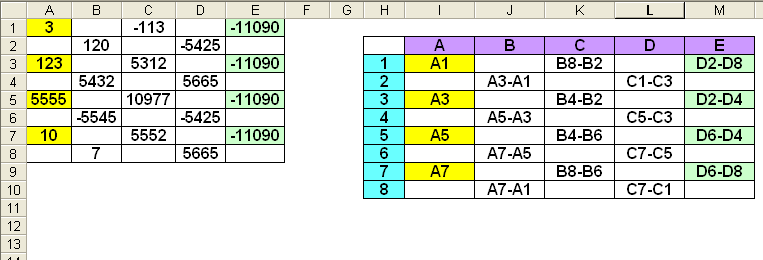
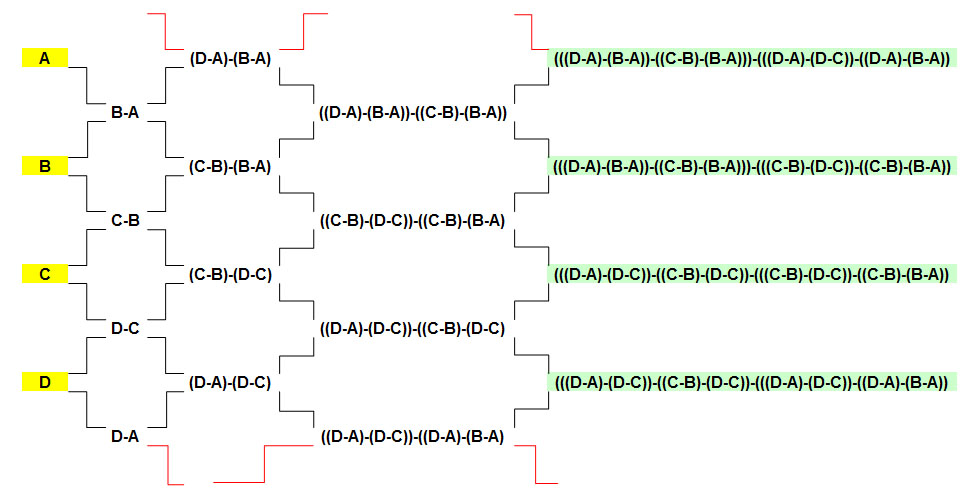
Chri, dans ton premier tableau, certaines fois tu fais la valeur d'en haut moins la valeur d'en bas, d'autres fois tu fais la valeur d'en bas moins la valeur d'en haut. Du coup, en développant tout, tu arrives dans tous les cas à 2D-2C, les autres composantes A et B s'annulant dans les divers parcours possibles.
Voici les équations d'après ton fichier (j'espère que je ne me suis pas planté...), il reste à développer...
Je n'ai pas refait avec ton fichier suivant ; on dirait qu'il n'est pas tout à fait pareil... -
Il y a un truc pas clair dans l'énoncé!

Je croyais que l'on faisait la différence entre le plus grand nombre d'un plus petit de deux voisins!
Alors qu'elle est la nouvelle règle ? -
@pilou said:
Il y a un truc pas clair dans l'énoncé!

Je croyais que l'on faisait la différence entre le plus grand nombre d'un plus petit de deux voisins!
Alors qu'elle est la nouvelle règle ?@PILOU
Tu as raison , je suis un escroc.
( j'ai surtout fait un loupé )@DareDevil
Bravo de m'avoir demasqué aussi vite
Si on fait "comme on a dit" sans partir sur des nombres relatifs , cela marche tout de meme .
(jusqu'a des niveaux variables selon la distribution des nombres de départ.
ci-aprés une égalité au niveau 10 .Tout cela ne me faisant toujours pas ma représentation graphique du phénomene !
Chri

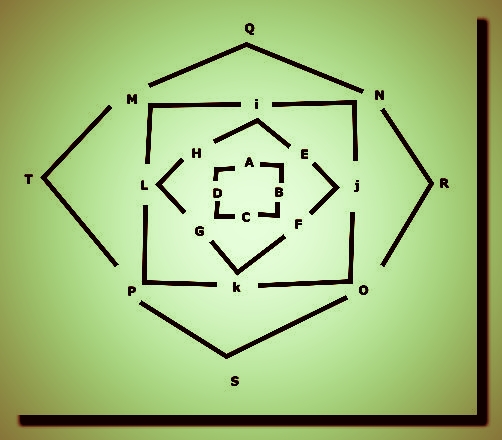
-
Tu peux remplacer le coin par une double flèche que sais-je!

Et ma règle, alors c'est quoi exactement ?

(les lettres n'ont pas de place particulières,
c'est juste pour montrer qu'un résultat est au bout de la pointe! )
Je trouve cela simple, économe et efficace!
-
@pilou said:
Et ma règle, alors c'est quoi exactement ?

La regle :
calculer la difference entre le + grand et le + petit pour ne travailler qu'avec des ecarts positifs .Chri
-
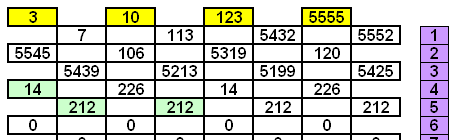
Bon, j'ai repris mes chiffres, je les ai ordonné
3 10 123 5555
et effectivement à la fin on arrive sur un même chiffre (4)
effectivement pas besoin de nombres négatifs!
7 113 5432 5552
5545 106 5319 120
5439 5213 5199 5425
10 226 14 226
216 216 212 212
0 4 0 4
4 4 4 4
et en calculant à la main on voit bien que cela ne peut que se
finir comme cela!
Les différences convergent et s'équilibrent!
(en plus je croyais que l'on devait y arriver en 5 étapes!
-
@pilou said:
Bon, j'ai repris mes chiffres, je les ai ordonné
3 10 123 55557 113 5432 5552
5545 106 5319 120
5439 5213 5199 5425
10 226 14 226
216 216 212 212
0 4 0 4
4 4 4 4Je dirai bien "5 étapes" .
Chri
-
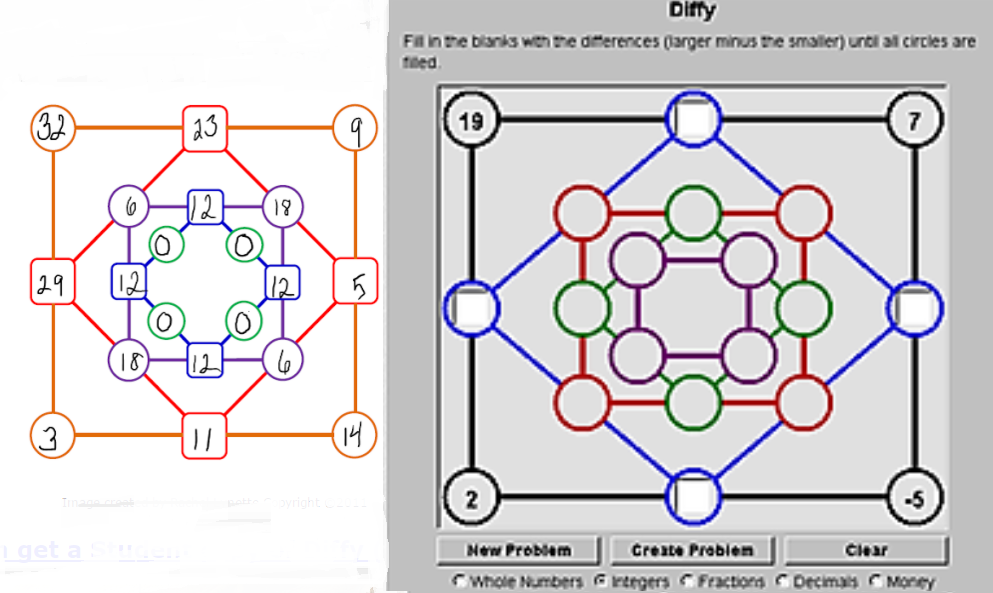
Comme le "cercle de Ducci" manquait sévèrement de référence sur le net, j'ai un peu fouillé et j'ai trouvé quelques liens :
http://images.math.cnrs.fr/Boites-a-differences-II.html
https://en.wikipedia.org/wiki/Ducci_sequence
http://www.math.grin.edu/~chamberl/papers/ducci_survey.pdfBon, il y a de quoi se triturer les méninges

-
@daredevil said:
Bon, il y a de quoi se triturer les méninges

Merci DareDevil
D'autres liens si on tape diffy game ...:
http://www.minds-in-bloom.com/2011/06/diffy-fun-subtraction-game.html
https://www.youtube.com/watch?v=F2aDuAIxjGcChri
-
@pilou said:
[...] Et j'ai l'impression que même si on se trompe une plusieurs fois
On finira quand même par y arriver si on devient plus attentif
car si j'ai bien compris toute configuration de 4 chiffres devient toujours gagnante!
On mettra juste plus d'étapes!
Encourageant ce jeu!
Bon, alors le jeu devient "comment prévoir le nombre d'étapes nécessaires pour arriver à 0 connaissant les 4 nombres de départ ?", ou pire "... si on admet une marge d'erreur 10% dans les calculs ?"

... bon, aller, je me remets sur mon cours de géométrie pour demain matin...

-
Ah, ils ont pris le même graphisme que moi!

Comme quoi le papier et le crayon, cela devient dépassé pour certaines choses!

Je ne devais pas être bien réveillé!
J'ai un peu tout mélangé vers la fin!Il faudra que je comprenne pourquoi j'ai mis 10 à 5439-5425!



Un dérapage dans un univers parallèle, sûrement!

Et j'ai l'impression que même si on se trompe une ou plusieurs fois
On finira quand même par y arriver si on devient plus attentif
car si j'ai bien compris toute configuration de 4 chiffres devient toujours gagnante!
On mettra juste plus d'étapes!
Encourageant ce jeu!
-
Autre chose à propos du tableur

Dans mes lointains souvenirs, il me semble pour ce genre de chose
on utilisait des fonctions de minimum ou maximum ou plus grand / petit
je ne sais plus les noms) voire même des comparaisons...
quand il y avait
des cases dont on ne savait pas à l'avance qu'elle était la plus grande ou la plus petite pour éviter les nombres négatifs!
Je ne vois pas ce genre de chose dans les codes proposés!

-
@pilou said:
Autre chose à propos du tableur

Dans mes lointains souvenirs, il me semble pour ce genre de chose
on utilisait des fonctions de minimum ou maximum ou plus grand / petit
je ne sais plus les noms) voire même des comparaisons...
quand il y avait
des cases dont on ne savait pas à l'avance qu'elle était la plus grande ou la plus petite pour éviter les nombres négatifs!
Je ne vois pas ce genre de chose dans les codes proposés!

Bonjour PILOU
Pour le calcul , j'ai utilisé la fonction suivante :
valeur absolue
=+ABS(B10-B4)
puisque que l'on travaille avec des nombres positifs et que l'on souhaite calculer l'ecart dans tous les cas . ( a>b ou b>a )Poiur le générateur de valeur , j'ai utilisé en plus :
valeur aléatoire ( de 0 a 1 )
arrondi a 0 décimales
=ARRONDI(ALEA()*100000;0)a+
-
Oh, douce mélopée des macro-commandes!

Oui cela semble bon!
- enfin tant que l'utilisateur n'entre pas des calembredaines!

Mais cela est une autre histoire!
Mais bon, je n'ouvre pas les tiroirs magiques de tous ces tableurs qui dorment dans un coin de ma machine!

Il me semble que j'avais fait un jeu de go avec ce genre de bidule...un essai car c'était une petite gageure de ne faire ça qu'avec 2 tableaux de cases!
- enfin tant que l'utilisateur n'entre pas des calembredaines!
-
Au sujet de l'énigme de la page précédente!

Bon voilà la solution, désarmante de facilité comme d'habitude!

Que je n'ai pas trouvé, ô rage, ô désespoir, ô vieillesse ennemie!
(enfin si, mais "manuellement" de manière plus que bidouilleuse et exténuante)Voilà d'où venait ce casse-tête!

@unknownuser said:
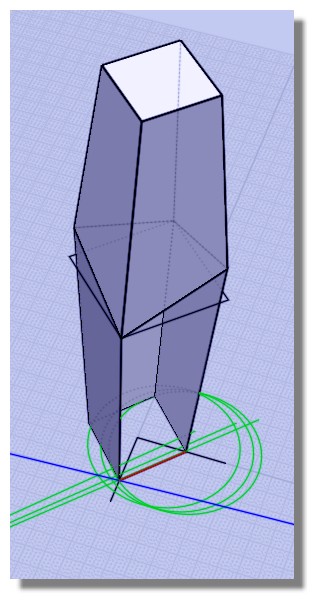
Pour la petite histoire, il s'agit des colonnes en béton qui servent de support aux extrémités d'un gigantesque pont sur lequel je travaille à Pékin. J'ai intégré l'équipe qui travaille dessus juste au début de l'étape "exécution". Donc le design général était déjà fini, il fallait peaufiner les détails, notamment au niveau du coffrage. Le collègue qui avait conçu les colonnes l'avait fait de manière très simple, en commençant par le losange du bas et le carré du haut, qu'il a ensuite reliés au centre sans se prendre la tête. A l'étape exécution, le bureau d'étude structure nous a informé du fait qu'il faut adapter les dimensions des colonnes en hauteur et en largeur pour que ça corresponde à certaines mesures bien précises. C'est de là qu'est née cette énigme, sur laquelle j'ai planché pendant des heures avec une collègue ingénieur pour finalement trouver cette solution en pleine nuit avant d'aller dormir!

Le point extérieur était le prolongement d'une des arêtes obliques du prisme supérieur
jusqu'à l'intersection du plan 0 !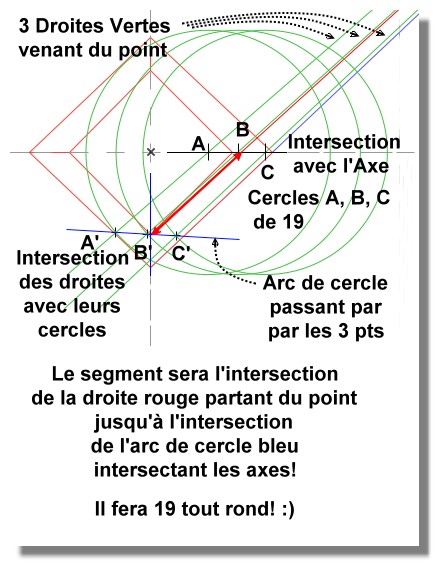
Advertisement







