CURIOSITE GEOMETRIQUES
-
Huhu: je viens de voir que je me suis planté en beauté!

J'ai complètement mal interprété la figure du "260" !
le carré ne fait pas du tout "260"
Tout à recommencer!
-
@unknownuser said:
résolu la partie haute par les maths et la géométrie
Je me casse la tête pour la trouver qu'avec les fonctions Taille, Ligne-Ligne ou Bouge!
ça doit être faisable!
Il suffit de simuler l'accroche visuelle des points chauds qui ne s'effectue pas!
A suivre!
Ici par Bear (qui n'a pas encore trouvé avec points chauds "snappés" )
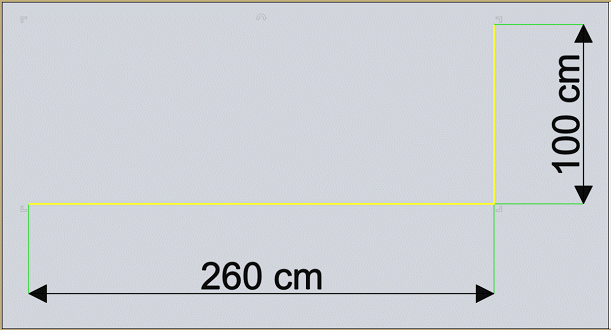
@unknownuser said:
Je positionne mon équerre à 600 cm de haut, peu importe l'emplacement exacte à l'horizontal pour l'instant. Puis je relie l'équerre au carré qui se situe à 1.200 cm de haut. Enfin, je réplique grâce à l'outil miroir le segment de l'autre côté du mât :

@unknownuser said:
Je sélectionne la "diagonale", je fais apparaître les points. Je sélectionne le point bas + l'équerre. Et là est le truc, le déplacement se fait en miroir :

@unknownuser said:
Il me reste à ajuster le haut de l'équerre avec la diagonale de droite grâce à l'outil "déplacer" (et en zoomant pour être plus précis):

@unknownuser said:
Mesurons le coté du carré qui sera à 600 cm de haut (mon calcul "théorique" fait apparaître 267,27 cm, le même résultat

-
Une solution qui ne plaira pas aux matheux mais qui va vite pour construire ce genre de truc si on n'est pas au 100/eme de mil.
Pour ce que ça vaut.
-
Je cherche toujours une astuce pour le problème du "snap" à l'oeil + Zoom!
j'en ai débattu avec Michael!
pour lui ce n'est pas simple à mettre en oeuvre rapidement, le temps de développement serait trop important!il nous reste donc à trouver des astuces de dessin "géométriques"!
Le truc fou, c'est que le snap se fait sur des formes déjà dessinées, ou des lignes d'aide que l'on dessineraient pendant l'utilisation d'une fonction!Le must serait bien sûr un snap pur et dur!
Là c'est toujours à l'oeil! Il suffirait de trouver une construction géométrique du point d'intersection pour avoir le Snap haute précision automatique!
Je continue les recherches! (évidemment la solution mathématique est exclue - il ne faut que du dessin!
Le point bas à droite ne sert à rien, c'est juste pour voir comment il bougeait!
Un mélange des fonctions Tailles, Ligne/ligne, Bouge devraient quand même le faire!
j'ai l'intuition que cela doit être d'une simplicité désarmante ... mais bon cela résiste encore!
Ce n'est que la rencontre d'un point avec une droite mouvante et le tout sur une ligne!
A suivre!
-
ça le vaut sûrement!

hélas je ne peux tester pour l'instant!
-
Dingue ça!

-
C'est pas clair ?

En français
C'est pas clair ?

Le commentaire du commentaire en français itou!
-
Ahhhhhhhhhhhhhh! Trouvé, c'était enfantin, merci les lignes d'aide
et la pure géométrie
je me donnerais des baffes de ne pas avoir trouvé plus vite!



-
Et bing la fin de ce cauchemar! :mrgreen
Bon, j'ai enfin trouvé une solution purement géométrique!
La clé était dans l'utilisation de la fonction Extrusion suivant une direction qui donne une facette plane!
On fait passer cette extrusion d'arête par un sommet d'un carré de 1919 du niveau Zéro
Cela donne un écart par rapport au carré 1919 niveau Zéro
On en pointe la moitié: ce qui donne le point de départ
On efface cette facette
on peut commencer la manipeExtrusion de l'arête par ce point ce qui donne une grande facette
Sur cette facette on dessine une Polyligne qui s'appuie sur les points "hauts"
et sur les points de l'intersection de cette grande facette dont on impose une longueur de 19
On vire la grande facette, on applique la Fonction Plan aux 4 lignes de la Polyligne
On a bien une face "Plane"
On s'appuie sur cette nouvelle Face pour faire une nouvelle grande face, un Polyligne etc..Le tout 4 fois pour boucler la partie basse
On groupe les faces de la partie haute, les 4 faces de la parties basses, la face du carré 19*19 du niveau Zéro
On obtient un "Solide" qui est la validation que tout ceci est bon! :itwasntme:Le fichier 3dm pour confirmer comme "solide" à surfaces planes!

Désolé d'avoir mis tant de temps mais cela était un peu casse-tête!

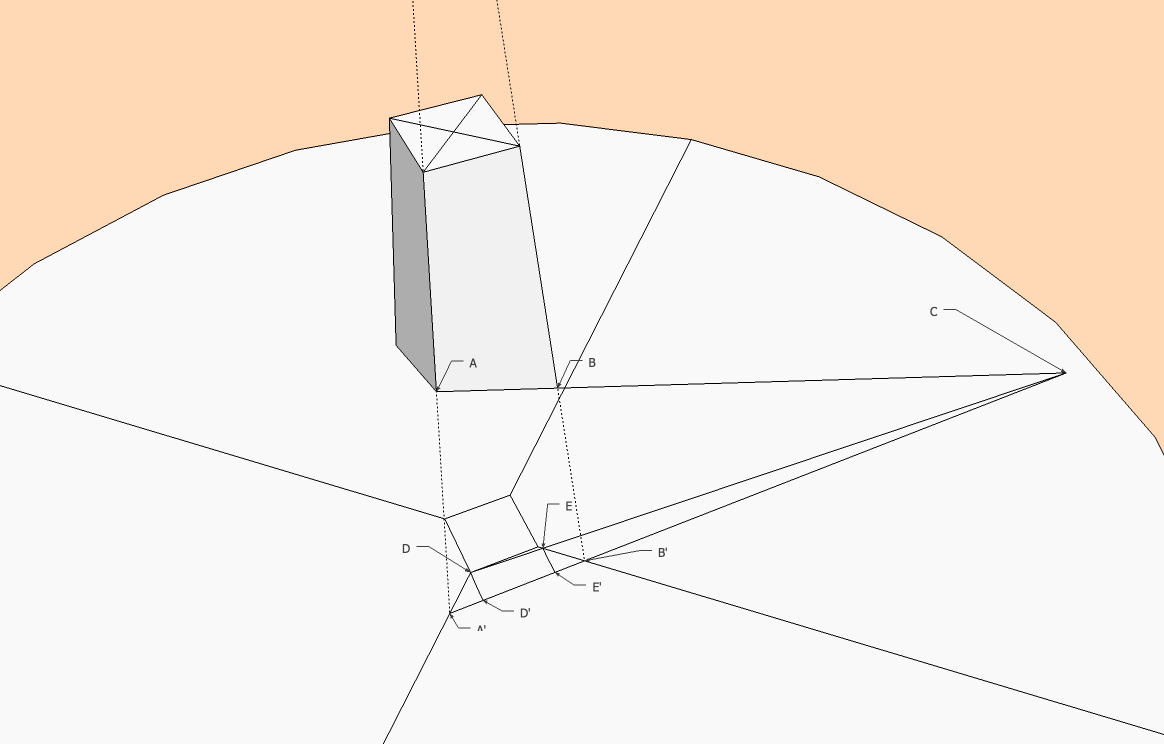
Les deux diagonales d'une facette basse en dimension /10
73,5955738
63,2385505
Figure qui montre "l'écart" d'avec le carré 19*19 niveau Zéro
Fonction Courbe/ Inter pour avoir l'intersection de la facette d'avec l'axe (Pt jaune)
Pointage de la moitié de cet écart

Extrusion suivant une direction par ce Point!

Dessin de la polyligne sur la facette avec imposition du côté à 19
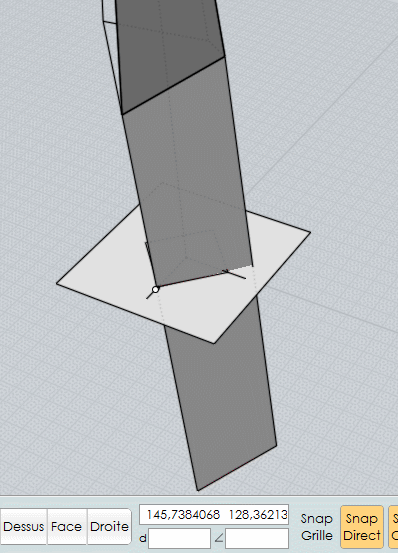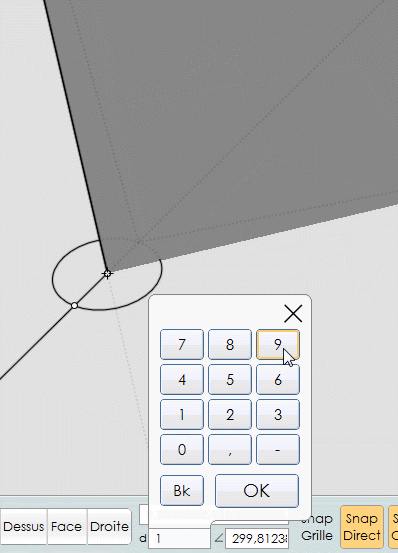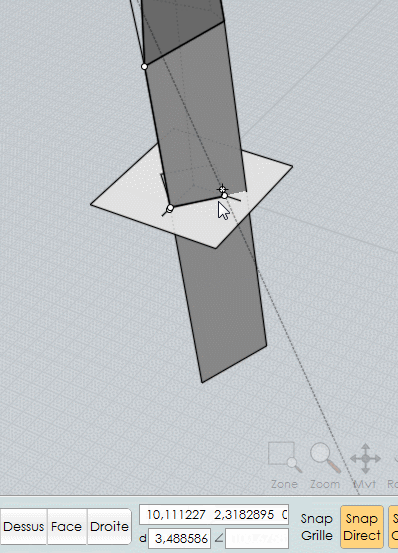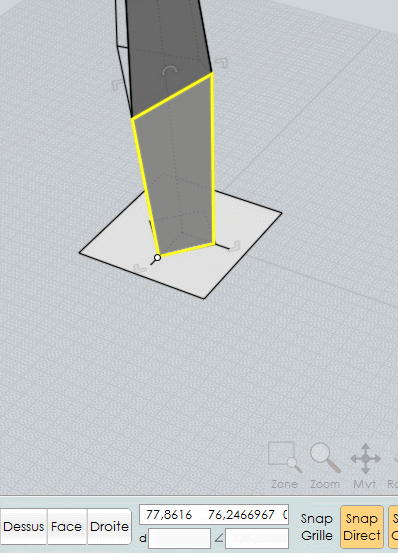
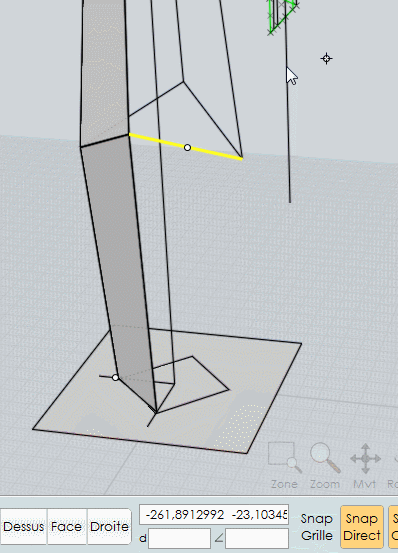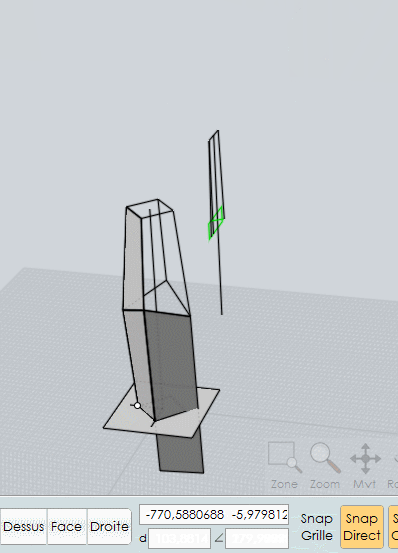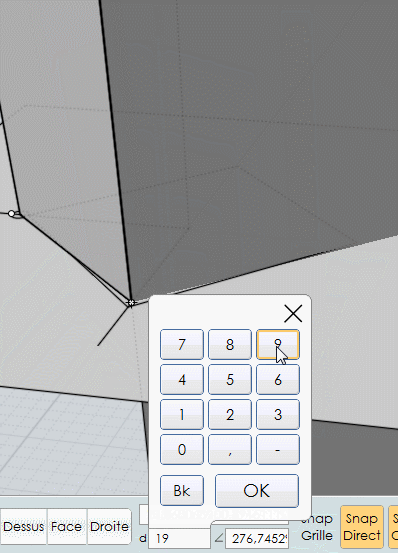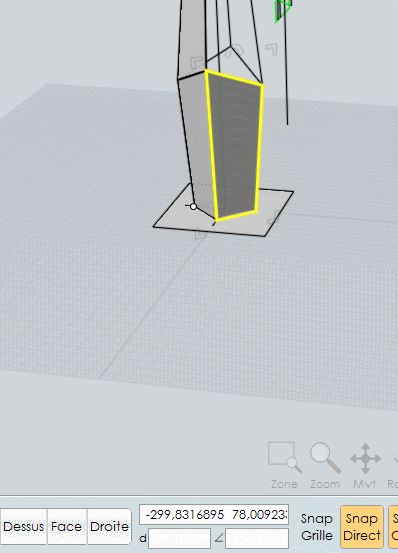
la 2ème face : on s'appuie sur la direction de l'arête verticale de la 1ère etc...
on pourrait faire ensuite un miroir de ces deux faces...j'ai fait 4 fois la construction...
-
Bonj
@PILOU
Bravo PILOU , beau boulot
j'aime bien le nom de ton fichier MOI
et si on passait a autre chose ... de plus facile pour se reposer
Trouves ci-aprés un extrait vidéo d'une curiosité géometrique .
Si quelqu'un souhaite dessiner un bloc sur cette base ...lien original :
https://www.youtube.com/watch?v=MYJkM4wfyZIChri

-
Oui, mais tout est à refaire!
les diagonales ne sont pas à 90°!
Donc tout à recommencer!
Il est costaud ce problème!
A suivre... -
@pilou said:
Oui, mais tout est à refaire!
les diagonales ne sont pas à 90°!
Donc tout à recommencer!
Il est costaud ce problème!
A suivre...Ce dessin va devenir notre fil rouge , faites entrer la vachette simone !
-
Les diagonales de la base sont hélas de longueurs différentes!
Et en plus ne font pas 90° entre elles!
Carré rouge de l'énoncé
quadrilatère bleu du résultat fallacieux!
Le fichier 3DM pour voir l'étendu de mon désespoir!

Pourtant j'étais pas loin et avec de vraies facettes "Planes"!


-
Là le résultat est bon mais...
le fichier en format 3dm
en dimension /10
Les demi-diagonales de la base sont égales deux à deux
12.7012448
et 14.13076Les deux diagonales d'une facette "basse" en dimension /10
73,5955738
63,2385505C'est un solide, mes facettes sont planes etc...
Là ou le bas blesse c'est que je l'ai trouvé "manuellement" !
Reste plus qu'à simuler ma manipe (je doute)
soit trouver une simple construction géométrique qui donnerait les deux points voulus!Donc c'est pas fini!


-
Au fait voici la version SKP
Je ne peux tester ce qui est envoyé ou converti, n'ayant pas la sauce tomate pour l'instant!
-
Voilà du cm (Moi) en Sketchup (cm) le tout en /10)
Donc la hauteur totale fait 120 cms
12,7012448 cms dans Moi devient 12,701245 cms dans SKetchup !
C'est pour cela qu'il vaut mieux pas faire de géométrie avancée dans Sketchup !
Ils n'ont pas le même nombres de décimales admissibles!
Et je ne parle pas d'intersection de cercle avec des droites!
-
Pour synthétiser!

Pour simplifier...dans le problème du dessus S =190 ou 19 pour moi

Facile avec solveur (gratuit Manu:el VF)... mais avec juste un programme de dessin...
S doit évidemment rester à sa longueur de départ!
A suivre...
-
@pilou said:
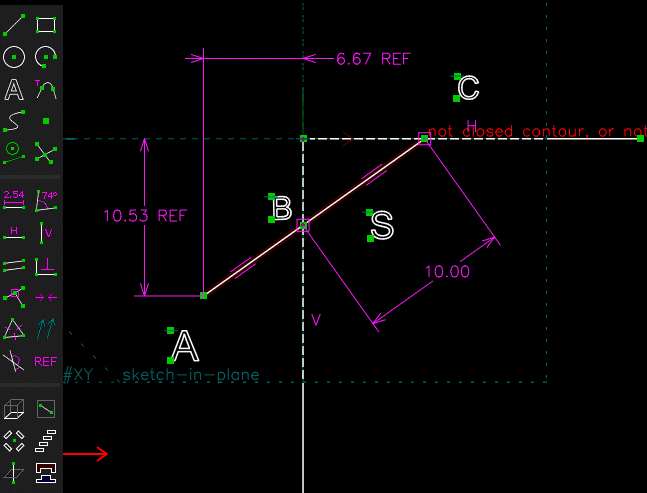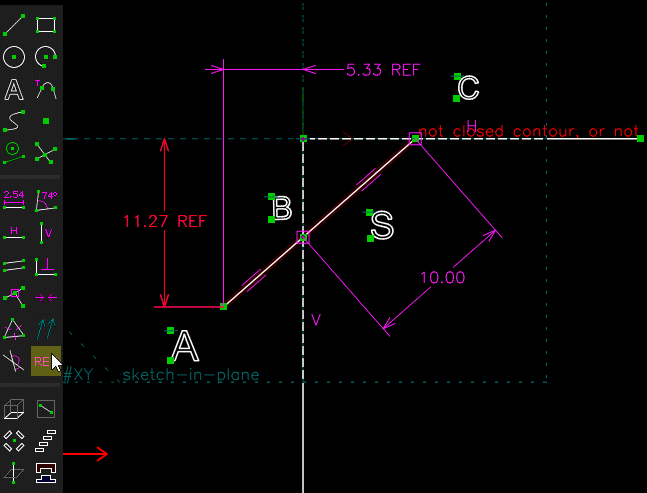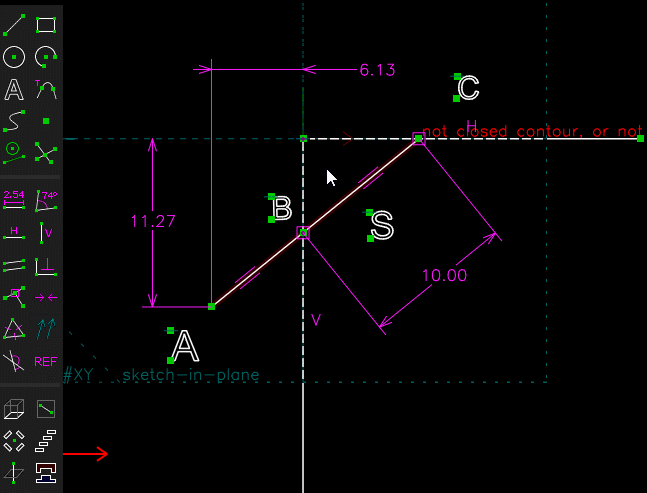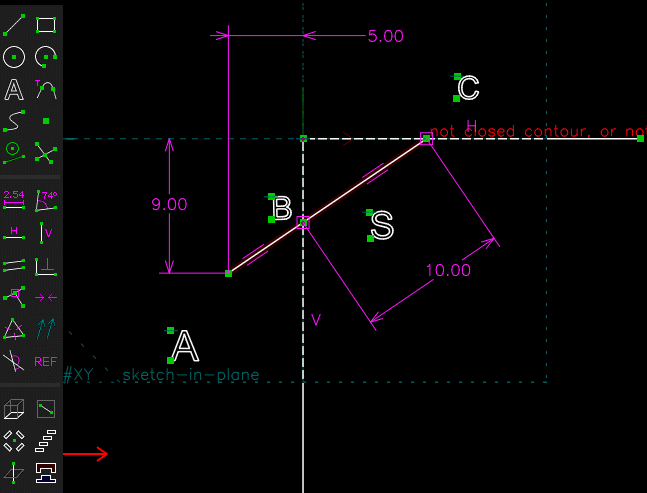
Facile avec SOLVESPACE
[highlight=#ffff40:16ugkal4]Cliquer sur l'image pour anime[/highlight:16ugkal4]r
( fichier .slvs joint en archive )Chri
-
bonj
Si on resume
notre question n'est-elle pas de trouver la position d'un plan tournant autour d'une de ses aretes et tangent a une sphere ?Chri
-
@ Chri tiens j'en avais un autre du Michael

Mais bon, je voudrais trouver une construction rien qu'avec Moi!

C'est le but du jeu!
Et je viens de voir en regardant le fichier SKP qu'il semble y avoir un petit
bidule de ma part!


Mais bon cela ne change rien aux manipes à refaire! Huhu!

Y a des chances que le "59.000" soit 60.000
Ma souris à recopié en diagonale à travers la grille!

Advertisement







