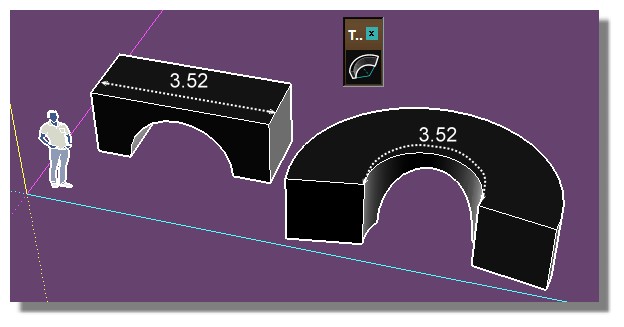
La véritable courbette! :)
-
-
Bonjour,
(1er message, j'espère ne pas faire d'impair)
Après de nombreux essais, je n'arrive pas à comprendre à quoi correspond la valeur qu'on rentre, le "bend" : ça n'est ni l'angle, ni le rayon, ni le décalage des extrémités...
Si tu as une piste ?
Bonne journée!
Camsone -
Sur mon image
C'est juste la longueur Hors Tout de l'objet considéré à un point donné!Ce qui veut dire que le pluging garde la longueur réelle dans sa déformation!
Dans le plugin lui-même je ne m'en rappelle plus il faudrait que je le relance!
Mon dessin de la 2ème image avait sûrement été fait à la va vite pour voir s'il y en avait qui suivait!

Les 2 cotes sont décalées!
 Il y a donc une de fausse sur mon image globale!
Il y a donc une de fausse sur mon image globale! 
Je vois que 2 ans après ça suit toujours!

Bravo pour la persévérance!
En tout cas un très bon plugin du sieur Thomthom!
Plus facile pour cette fonction que le Fredo Scale de Fredo! -
Bon, j'ai relancé la bête!

Est-ce plus clair ?
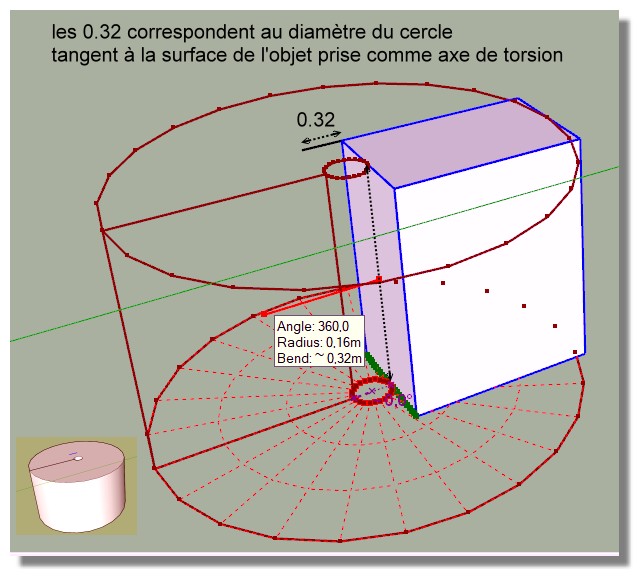
-
Pour les variations

IL vaut mieux prendre un composant qu'un groupe car on peut ainsi changer les axes
qui influeront sur les directions de courbature!
Ou alors carrément pivoter d'abord l'objet ça évite les prise de tête!
-
Merci beaucoup pour ta réponse!
OK j'avance dans la compréhension, quand on plie avec un angle de 360° effectement on a la valeur de "bend" qui est égale à 2 x le Radius.
Mais quand on fait une courbure avec un autre angle, je ne retrouve pas ce rapport → voir image jointe.
J'ai rentré un "bend" de 100mm, et je ne retrouve pas cette valeur dans l'objet courbé.J'ai essayé plein de valeur pour "bend", et je ne comprends pas à quoi ça correspond.
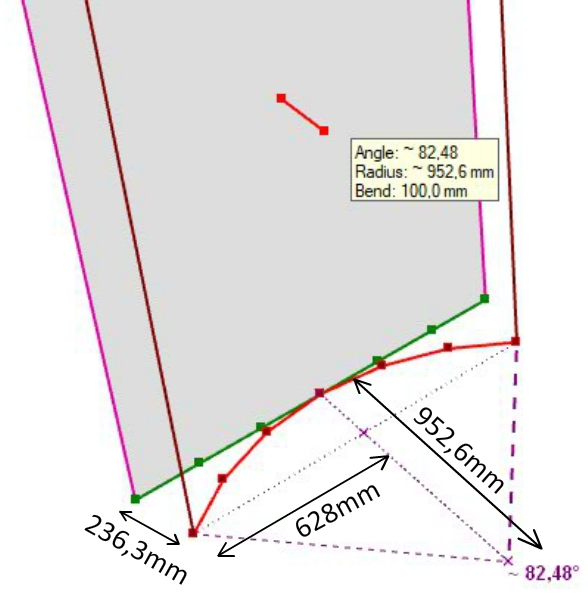
-
C'est la longueur de la largeur maxi de la surface qui va être transformé en cercle!

Qui sera bien sûr la longueur maximum de ce "Bend", donc le diamètre du cercle pour une courbature de 360°!

Est-ce plus clair ?

Je ne sais combien fait le segment"Vert" mais en sachant les valeurs données dans la fenêtre d'infos, avec une petite règle de 3 on devrait pouvoir le retrouver

-
(pour répondre à ta question, le segment vert de ma première image fait 1371,3mm)
Et bien non désolé, je n'ai pas encore bien compris.
Pour un angle de 360° OK, on a bend = diamètre. Mais pour tout autre angle que 360°, je ne vois pas à quoi correspond sur le dessin la valeur du bend.
Sur cette deuxième image, j'ai pris un carré de 1000x1000, et j'ai fait une courbure à bend = 100mm, et un autre à angle = 360°.
Sur le carré plié à bend = 100mm, je ne mesure rien qui fasse 100mm ?

-
Mais non!

Si on prend un volume d'arête 3.14m (Pi)
on va avoir pour 360° un "bend" de 1.00m
Les autres valeurs de ce "bend" ne seront que la déclinaison de 0 m à 1 m pour 0° (rien) à 360° (tout)
C'est donc un genre de pourcentage! 0.50m va donner 180°

0.25m va donner 90°, 0.75m va donner 270°, 1.0 m va donner 360° etc...
Est-ce plus clair ?
Cette valeur de 1.m dépendra de la valeur de départ de l'arête du volume considéré!
Et donc totalement différent pour autre volume!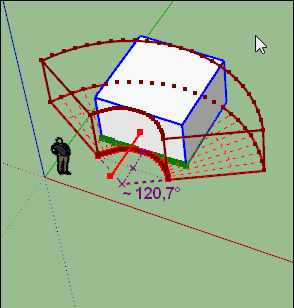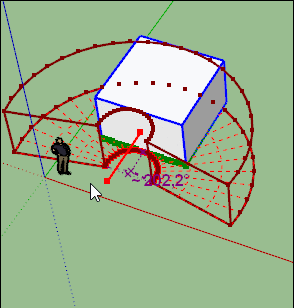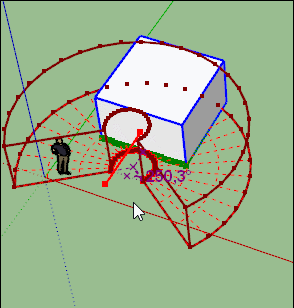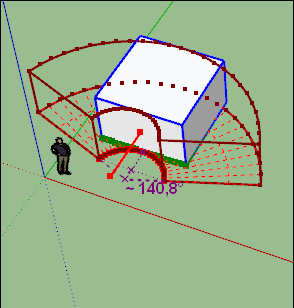
-
Ok je comprends que ce bend est un ratio, et qu'on ne peut pas le mesurer sur le résultat (en dehors de 180° et 360°).
J'ai regardé la forme de la courbe du rayon par rapport au bent, et ce n'est pas une relation linéaire, on ne peut donc même pas faire de produit en croix.
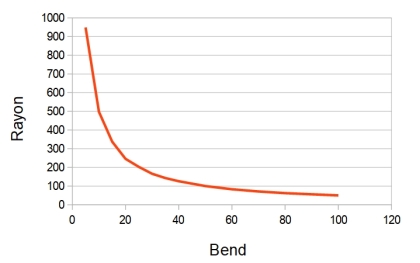
Dommage car ça m'aurait arranger de pouvoir demander à l'outil une courbure de x mm vers l'avant par exemple.Merci en tout cas pour toutes ces explications!
A bientôt
-
J'avoue ne pas saisir le problème!

Si maintenant mon "arête" de mon objet fait 1m
le "bend" va faire 32 cm pour 360° (2PiR = 1m) 2R = 0.318 = 32 cm
24cm pour 270°
16cm pour 180°
8cm pour 90°
4cm pour 45°
etc...et de toute manière je ne vois pas trop à quoi sert de maîtriser ce "Bend"
puisqu'on peut rentrer directement l'angle voulu !
Et si on veut une avancée de 1 cm et bien on trace cette distance en vue de dessus
et on aligne le "Bend" dessus!
Ce qui fait ici un angle de 4,6° pour mon objet global considéré!
On doit aussi pouvoir faire une résolution par une règle de 3 mais je n'ai plus l'inspiration!

-
OK je suis d'accord avec le lien entre Bend et angle, mais ce n'est pas ce lien qui m'intéresse, c'est le lien entre Bend et le décalage de la ligne de base de l'objet.
En fait j'aurais pu exprimer ma question de cette manière :
j'ai un objet de 720mm de large, j'aimerai le courber de 120mm, comme ceci :
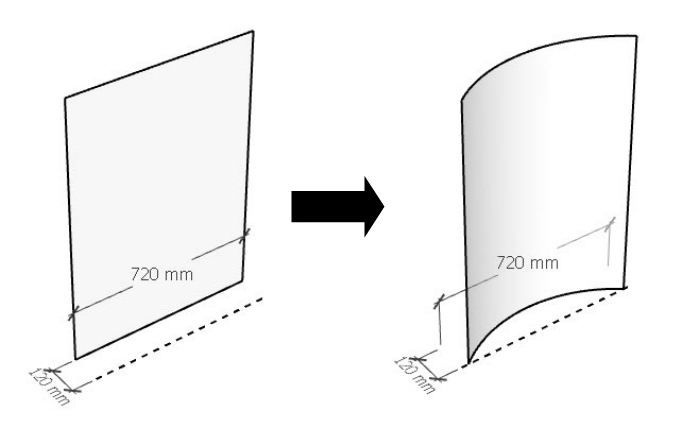
Est-ce qu'on peut rentrer une valeur pour arriver exactement à cette courbure de 12cm? Et si oui quelle est cette valeur?
Merci de ta persévérance

-
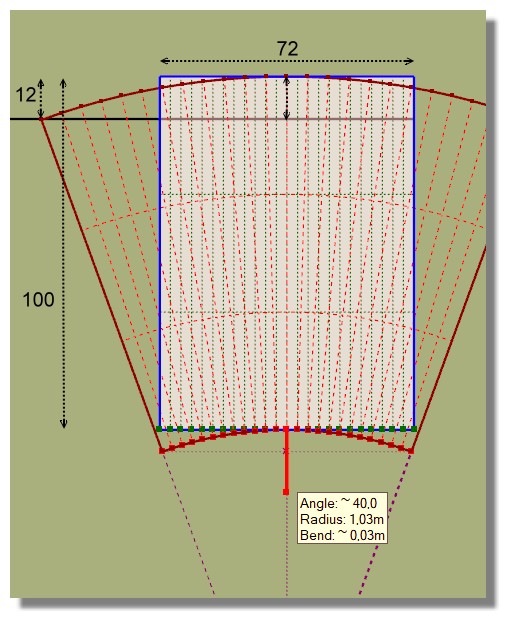
Oui mais il manque une donnée, la longueur de l'objet! (l'épaisseur si en 3D)
Avec ma méthode visuelle quasi 40°
Mais cela dépend aussi de la longueur de l'objet (ici 1 m d'épaisseur )
C'est donc une donnée "variable" !
Encore la flemme d'en trouver une résolution : sera de toute manière moins rapide que la résolution visuelle pusiqu'il y aura un calcul à effectuer donc à rentrer!
Ici il n'y a qu'à dessiner une simple ligne!
Dommage que les points chauds ne marchent pas entre les points rouges du plugin et la géométrie de l'objet!
-
@pilou said:
Oui mais il manque une donnée, la longueur de l'objet! (l'épaisseur si en 3D)
Ici mon objet n'a pas d'épaisseur, c'est une surface.@pilou said:
Avec ma méthode visuelle quasi 40°

OK j'ai compris, approximation visuelle, mais pas de valeur exacte. C'était tout le sens de ma question en fait, est-ce qu'il y a moyen de rentrer une valeur exacte, ou bien faut-il faire par approximation visuelle. J'ai ma réponse.
J'ai fait une approximation visuelle pour mon exemple, et avec quelques essais je trouve une valeur de bend de 50,6mm, pour avoir ma courbure de 120mm (environ
 ).
).
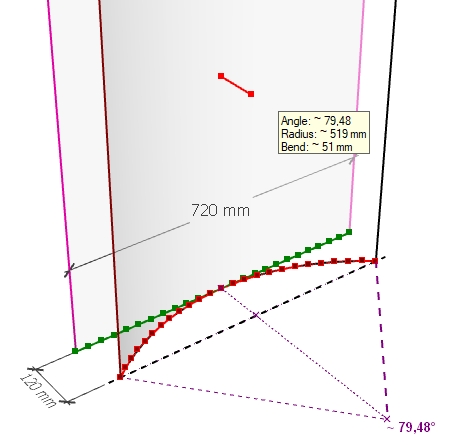
Merci pour les explications!

-
Comme à priori la seule valeur que l'on peut rentrer c'est l'Angle il va bien falloir s'en contenter!

Par contre on doit pouvoir rentrer une valeur d'angle ultra précise pour avoir la valeur du Blend acceptable! (pas encore penché sur le sujet, ça doit être facile, enfin j'espère)

Pendant qu'on est sur le True Bend je viens de trouver un BUG!
On ne peut faire de courbure sur des courbes simples parallèles aux axes!

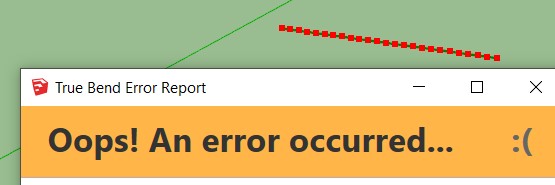
Quand elles sont quelconques ça marche!

-
Bonsoir
Je ne trouve pas de formule donnant directement le résultat, mais, de proche en proche, je trouve, pour avoir les 120 mm demandés, pour un angle de 79,536° un arc de cercle de 720,005459 mm et un rayon de 518,674236 mm.
Si tu as besoin de la méthode pour l'utiliser dans d'autres cas, je peux mettre le fichier excel correspondant en pièce jointe...
@ plus
-
@pilou said:
Comme à priori la seule valeur que l'on peut rentrer c'est l'Angle il va bien falloir s'en contenter!

On peut rentrer le Bend en ajoutant l'unité de distance, par exemple 50,6mm dans mon exemple. Pour rentrer un angle → ajouter l'unité d'angle, par exemple : 30deg, et pour changer le nombre de segments → ajouter s, par exemple : 6s.
@ciscoo said:
Si tu as besoin de la méthode pour l'utiliser dans d'autres cas, je peux mettre le fichier excel correspondant en pièce jointe...
Ha oui je veux bien!
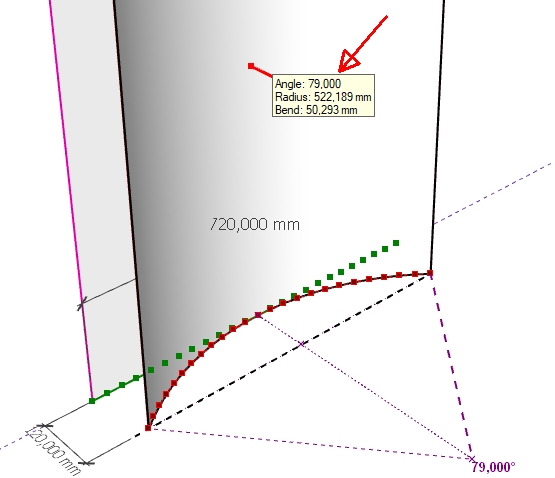
Par contre je me rends compte d'une nouvelle difficulté, quand on rentre une valeur d'angle avec des décimales, TrueBend arrondi à l'entier. Par exemple quand je lui indique 79,536deg, il arrondi à 79,00 ...?
Alors on peut indiquer la valeur du bend, qui lui garde ses décimales a priori. As-tu la valeur du bend dans ton fichier excel? Dans mon exemple, il serait autour de 50,63mm.
Merci! -
Ah bé si en plus on peut rentrer le "Bend"! Excellent !

On peut mettre 3 chiffres après la virgule pour un angle!
Mais il faut le paramétrer dans les unités angulaires des préférences!
(enfin c'est comme cela pour la 2017!
-
Bonjour
Cf. en pièce jointe
Il faut écrire autant de valeurs d'angle dans la colonne A que désirées jusqu'à obtenir la valeur SA voulue dans la colonne C.
@ plus
-
@pilou said:
Ah bé si en plus on peut rentrer le "Bend"! Excellent !

Et oui c'est pour ça que je parle du bend depuis le début

@pilou said:
On peut mettre 3 chiffres après la virgule pour un angle!
Mais il faut le paramétrer dans les unités angulaires des préférences!
(enfin c'est comme cela pour la 2017!
Chez moi (en 2019) ça ne marche pas, même en paramétrant les unités, quand je rentre 79,536 par exemple il ne garde pas les décimales :
Super ton fichier Ciscoo! Merci!
C'est très clair, par contre si je n'arrive pas à résoudre le problème des décimales d'angle non prises en compte par TrueBend, il faut que je puisse rentrer la valeur du bend.
Penses-tu pouvoir ajouter une colonne avec le bend dans ton tableau? Ça serait l'idéal
Advertisement