CURIOSITE GEOMETRIQUES
-
Vidéos d'Oskar van Deventer sur YouTube
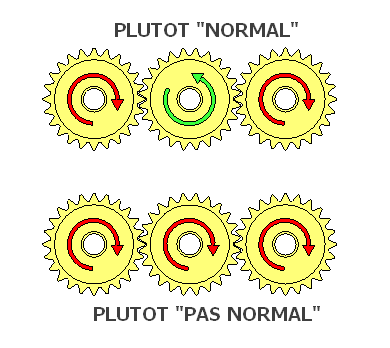
Dans cette vidéo exemple , sont présentées 3 roues "dentées" qui s’engrènent et tournent donc successivement sens horaire / anti horaire / horaire ( normal)
Après avoir retournée la pièce médiane .... les roues tournent alors toutes dans le même sens ( et la ... c'est MOINS normal
 )
)Pour info , ces types d'engrenages sont appelés PARADOXAUX
https://fr.wikipedia.org/wiki/Engrenage#Engrenage_paradoxal[highlight=#ffffbf:pr3lrogw]Je ne vous parle même pas des autres vidéos d'Oskar. Je suis Oskar addict
 [/highlight:pr3lrogw]
[/highlight:pr3lrogw]Chri


-
Huhu Sacrément futé l'Oscar!

Bel exercice pour le nouveau MSPhysics et le SUbD pour la modélisation!
Cliquez sur l'image pour voir l'animation!Sinon, moi je suis dans le potage!
Si la construction montrée au-dessus fonctionne pour le cas considéré, j'avais fait des essais rapides et avait déduit rapidement que la solution était universelle quelque soit le point de départ, et la distance demandée!Et bien hélas il n'en n'est rien!

Donc il y a des chances qu'il reste à trouver une autre solution "géométrique" universelle!
Ce n'est pas mon résultat idylique montré ci-dessous!
(Désolé, j'ai pas retraduit mon sabir)
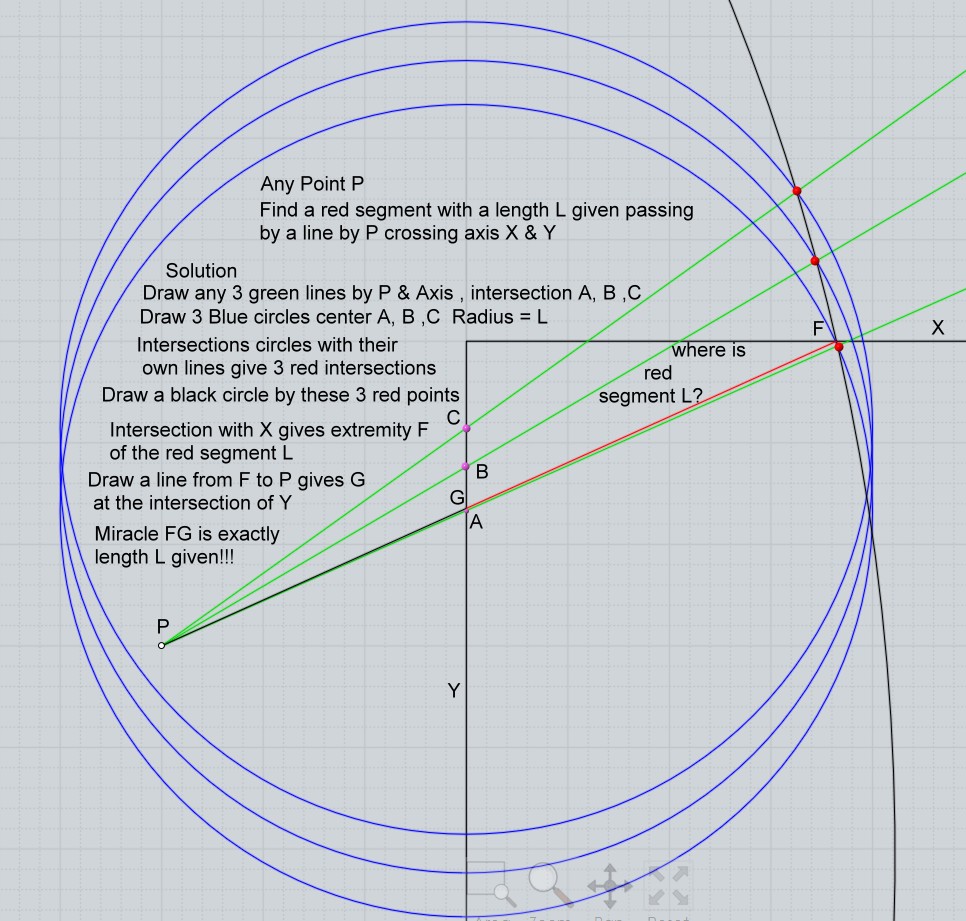
Un contre exemple

-
@pilou said:
Cliquez sur l'image pour voir l'animation!
Bonjour PILOU
Objets inanimés, avez-vous donc une âme... (Lamartine)En l’occurrence , celui-ci me parait bien fixe!

Chri
-
Effectivement y a du louche!

Le temps a suspendu son vol!
Et vous heures propices suspendez votre cours!
Voici donc le post original!
-
Bonjour
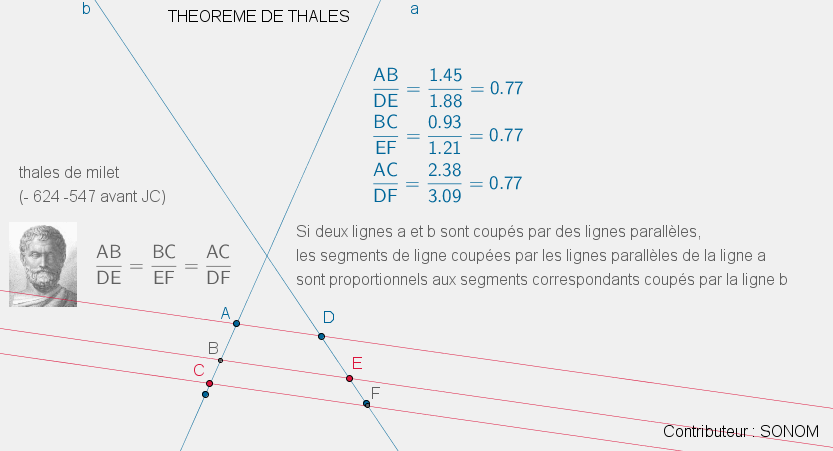
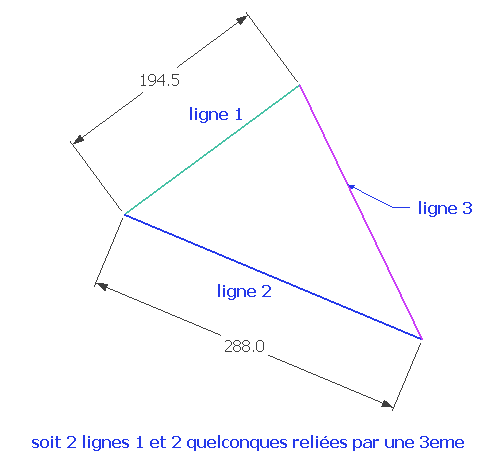
Trouvez ci-joint un petit rappel du théorème de THALES .
Piqué et francisé depuis ce lien GEOGEBRA :
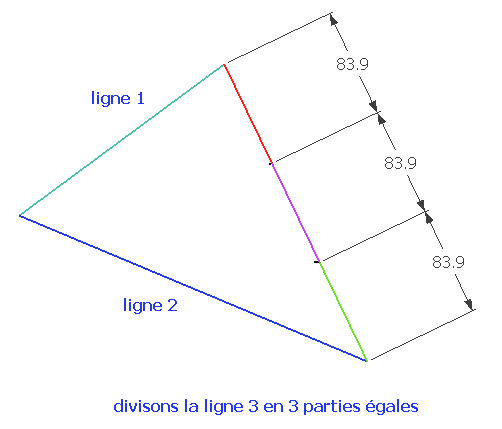
http://tube.geogebra.org/user/profile/id/16455?lang=enAprès cette petite révision , je vous propose les 4 petites manip suivantes .
Chri
-
Bonj
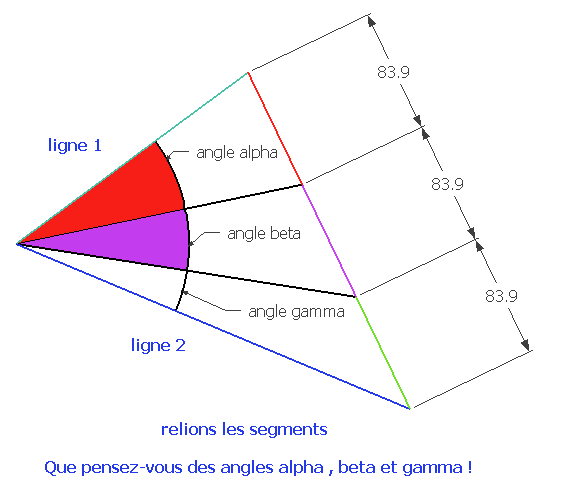
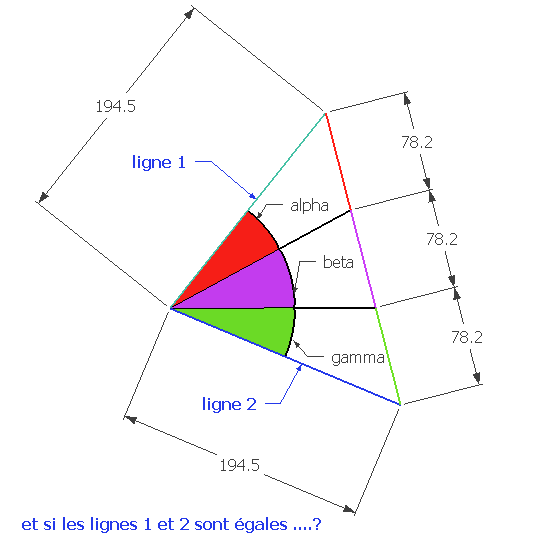
Est-ce que vous n'auriez pas imaginé des angles alpha , beta et gamma égaux ?
Si vous découpez une tarte , le choix de la part BETA ne le sera pas tant que ça !
Vous êtes maintenant prêt pour surfer , le thème du jour étant la trisection .
Chri
-
@pilou said:
Conway est mondialement connu ...]
Ce qui est moche pour lui, c'est qu'on parle "meme pas" de son cercle dans wikipédia !
-
Conway est mondialement connu pour avoir inventé le jeu de la vie!

La meilleure implantation! (août 2017)
 (c'est gratuit)
(c'est gratuit) 
http://golly.sourceforge.net
-
Ils ont leurs têtes de gondole chez wikipédia!

-
Bonjour
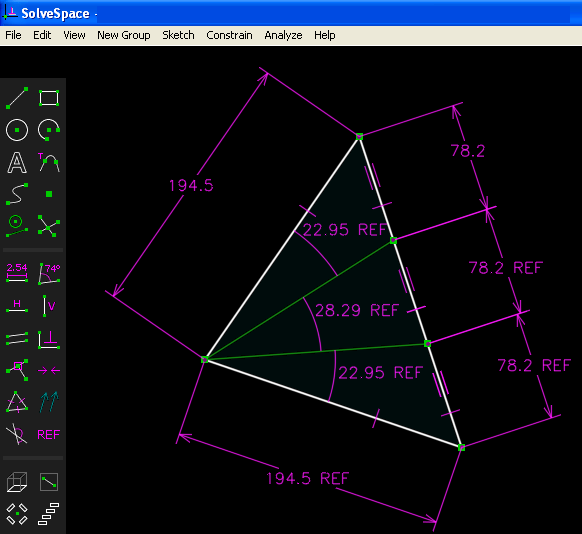
Quelques figures sympa ( curiosité 1 sur 4 du 29/09/2017 )
Triangles d'aires constantes
-
Bonjour
Quelques figures sympa ( curiosité 3 sur 4 du 29/09/2017 )
partage du carré en 5 parties égales
( I, J, K et L sont les milieux des côtés d'un carré ABCD )Lien :
http://debart.pagesperso-orange.fr/seconde/carre-5-fois-petit.html#ch4b
-
Bonjour
Quelques figures sympa ( curiosité 4 sur 4 du 29/09/2017 )
cercle de CONWAY
( le centre du cercle est le point de concours des bissectrices )Lien :
http://www.maths-et-tiques.fr/index.php/detentes/conway
-
Bonjour
Quelques figures sympa ( curiosité 2 sur 4 du 29/09/2017 )
partage du parallélogramme
cliquer sur le lien suivant pour manipuler.lien :
http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/kangourou/parallelogramme.html
-
Bonsoir PILOU
Qu'est-ce que tu pense de :
wx = yz !
-
Ma méthode nettement plus fun avec Moi qui évite toutes ces élucubrations mathématiques! : cercle par 3 points!
 On est au 21ème siècle!
On est au 21ème siècle! 
Et économie de cachets d'apirine!
( Je n'essaie même pas avec SketchUp qui fait des cercles "carrés" !
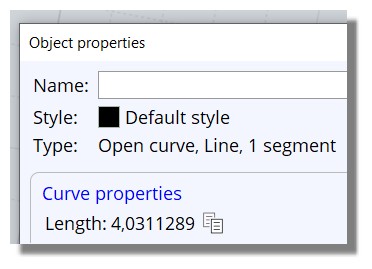
Je trouve Rayon = Distance= 4.03 (regardez dans le petit cadre sous la figure) parce que j'ai demandé que 2 décimales dans les paramètres!

Si j'en demande plus j'ai cela

La méthode plus que simplette et 100 fois plus rapide!

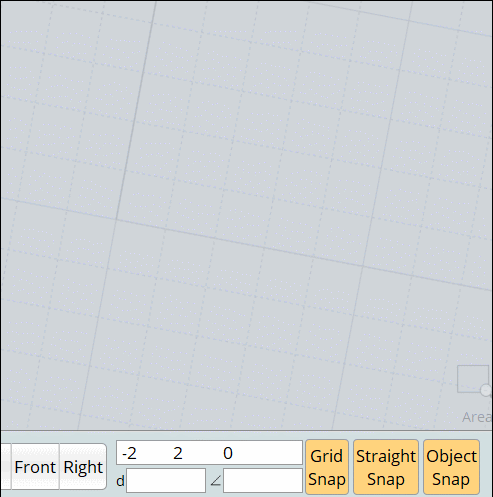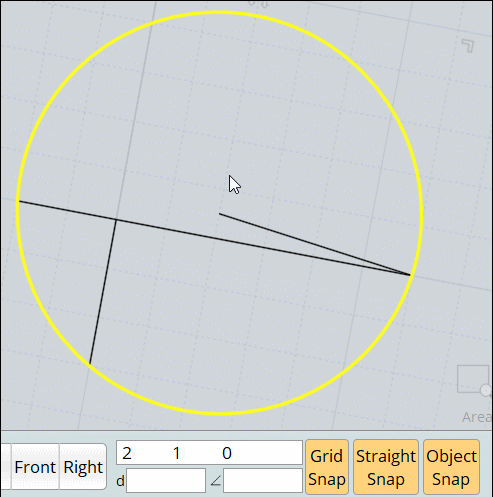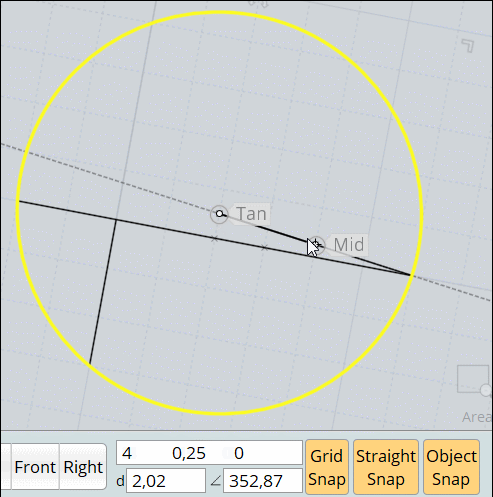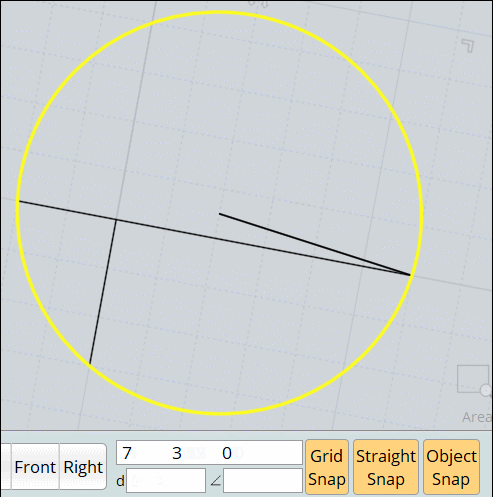


-
Je dis que c'est très malin, mais très analythique!

j'ai le cerveau en compote il me faut de l'hyper simple ayant largement dépassé l'âge pivot!
-
On nous cache tout, on nous dit rien!

-
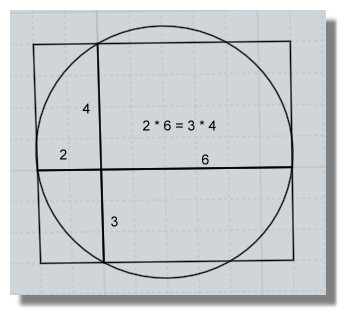
C'est juste une resuçée de celà !

On avait appris cela au collège!
(sélectionner le texte / clic Droit aller à l'adresse Web...pas moyen de faire un lien qui marche!
https://fr.wikipedia.org/wiki/Identité_remarquableOn a juste rajouté le cercle dessus qui passe donc par 4 points remarquables!

-
REPONSE DE GERARD VILLEMIN ... que je remercie.
C'est une relation classique (théorème des cordes sécantes), valable même si les cordes ne se coupent pas à angles droits
Voir ma page en http://villemin.gerard.free.fr/GeomLAV/Cercle/Puissanc.htm#cordes

Cercle - fondements
Nombres, curiosit�s, th�orie et usages: cercle, ses propri�t�s de base, fondements, d�monstrations
(villemin.gerard.free.fr)
Cordialement
Gérard Villemin
Pour votre information, voici l'adresse du
site aiguillage pointant sur tous mes sites
http://villemin.gerard.free.fr/index.html.
-
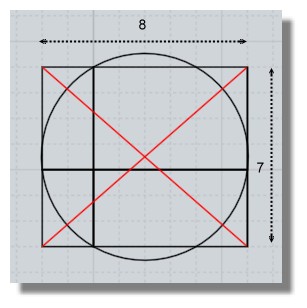
Et si on trace les diagonales du rectangle général 7 X 8
avec les mêmes dimensions qu'au dessus 2 + 6, 3 + 4Devine où elles se croisent ?

C'est encore une démonstration que je préfère à l'analythique!
Attention le cercle déborde aussi légèrement à l'horizontale de ce rectangle, ce serait trop beau!

Advertisement








