Perdu dans mon dessin et dans le forum :)

chri

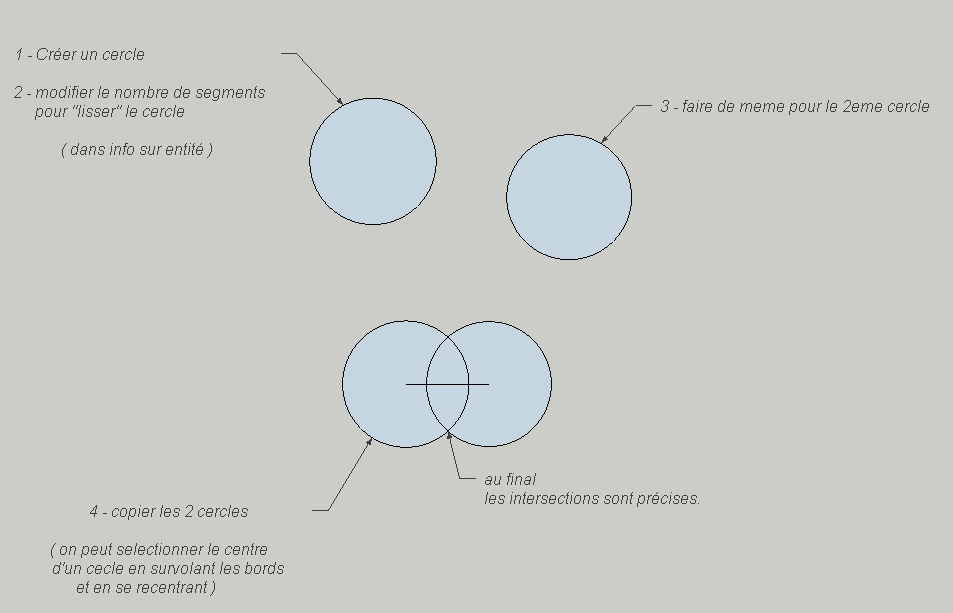
Sur ma planche, un trait deux cercles et l'intersection me donne l'orientation des deux autres côtés, mais voilà je n'arrive pas à trouver l'intersection de deux cercles, car les cercles sont constitués de segments et je tombe systématiquement sur une extrémité, et même en traçant un cercle à 720 segments je n'obtiens pas la précision désirée, ce qui m'étonne tout de même, il doit bien y avoir une astuce que je ne trouve pas.
Si vous pouviez m'aider, je vous en remercie d'avance.

%(#008000)[Salut Guy

je te propose la manip. suivante illustrée par 2 fichiers .
dessines bien

Christian]

INTERSECTIONS AVEC CERCLES.skp

INTERSECTIONS AVEC CERCLES.png

gilles

Un petit tour du côté de chez TIG, TRUE TANGENT ( vraie tangente pour les anglophobes)
http://forums.sketchucation.com/viewtopic.php?t=19457#p160780

Guy54110

Merci Christian pour ta réponse rapide,
C'est bien ainsi que j'avais procédé mais le résultat ne me plaisait pas trop, car mon erreur fût de trop segmenter le cercle (720 ça fait des petits segments).
Et je croyais trouver une intersection alors que c'était une extrémité et aucune différence avec les extrémités de segments.
Je viens de faire l'expérience de couper ton cercle à 300 segments par un simple trait et l'info me donne aussitôt 301 segments, donc l'intersection est bien placée mais remplacée par une extrémité, suffit de zoomer et choper la bonne extrémité.
Avec tous mes remerciements pour m'avoir aider à réfléchir et y voir un peu plus clair.

Le lien à Gilles sur "TRUE TANGENT" c'est super mais c'est pas pour moi pour l'instant, mais je garde de côté pour approfondir.
Bonne continuation à tous, peut-être à bientôt
GUY

pilou

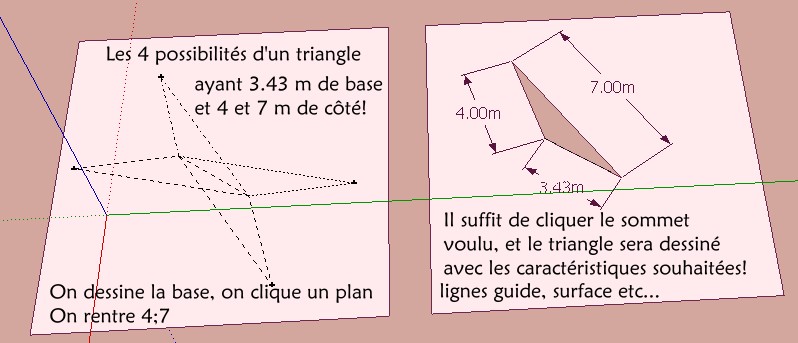
Sinon il a cela Trilatération by Didier bur!
Commande de construction de triangle dont on connait les dimensions des 3 côtés
le trait = le premier côté
cercle 1 = 2ème côté
cercle 2 = 3ème côté
Très complet!
Choix du plan, garder surface, lignes guides etc!Documentation inside!

PS Sinon pour ce genre de chose il vaut mieux commencer un nouveau sujet que de le mettre à la suite!
Cela drainera plus de monde sur un sujet précis

pilou

En image
Ici la variante haut gauche voulue!
Et pas un cercle de dessiné! Que de la trigonométrie cachée pour l'utilisateur
Merci Didier!

Jean Lemire

Bonjour.

Mon message précédent était pour proposer une méthode ultra simple pour répartir N objets autour d'un cercle sans avoir à effectuer aucun calcul.

Il s'agit de spécifier 360° comme angle de rotation et ensuite le nombe de copies voulues avec un signe / pour répartir uniformément les copies entre la position de départ et la position d'arrivée.

Évidemment, la copie va se retrouver exactement sur l'original et sera fusionnée avec ce dernier, à moins que l'objet en question ne soit un groupe ou un composant, auquel cas, il faudra supprimer l'original ou la copie, peu importe laquelle.

Par exemple, avec 14 objects, le calcul de 360 divisé par 14 donne un angle de 25.714285714285714285714285714286... C'est assez long à entrer dans la fenêtre des dimensions et de toute façon la précision de SU ne va pas si loin. S'il y a un arrondi, il y a donc un manque de précision et donc une minuscule erreur. Le cumul de ces petites erreurs est suffisant pour que ls nème copie ne soit pas bien positionnée.

Je préfère donc laisser SU faire le calcul et positionner les objets lui-même.

Salutations.

Borishusser

Bonjour tout le monde,
et bonjour Jean,

C'est bien ce que j'avais fait dans un premier temps. En reprenant ta proposition initiale de faire le volume juste sur un segment puis de dupliquer le segment, avec un Cercle de 14 segments j'avais un moyeu plus proche du carré qu'autre chose alors j'ai distingué les trous de la pièce, et la répétition de l'angle depuis un segment de 360/14 créait un défaut flagrant au dernier trou. Pourtant en faisant la même chose avec 360/28 mais en ne prenant qu'un trou sur 2 c'est impeccable... Je ne me l'explique pas, mais ça marche
Je n'ai pas encore pu attaqué les rayons, mais vous aurez surement des nouvelles

Et puis, comme d'habitude: merci tout le monde !

Borishusser

Bon, au moins c'est allé vite, tellement que je n'ai pas atteint les rayons !!!
Sur l'ensemble de la roue les rayons se répartissent bien sur pasr côté, mais aussi en rotation. Les trous d'un côté du moyeu ne sont pas en vis-à-vis mais décalés d'un demi espacement entre trous (euh...c'est clair, ça ?).
Bref, les cylindres, constitués de segments, ne s'alignent plus, provoquant des ouvertures.
Ah non excusez-moi j'ai trouvé: je fais tourner les trous au lieu de faire tourner la pièce !
Désolé du dérangement

Borishusser

Hé hé !

Borishusser

J'en suis à dessiner les trous pour la jante. Et de nouveau la répétition pose problème. La division ne colle pas...

trous.skp

gilles

Le plus simple pour ce genre de pièce est de travailler sur un quartier, en l'occurrence un 14 ème, en faire un composant, le dupliquer pour obtenir l'ensemble du moyeu et faire les modifications en éditant le composant; toute les modifs se répercutent en temps réel sur toutes les instances on gagne aussi beaucoup de temps.

eddy

Salut, ta jante fait quelle diamètre et combien de trous il faut sur le périmètre.

Borishusser

Mmmmmh! Ca sent la réalisation, ça !
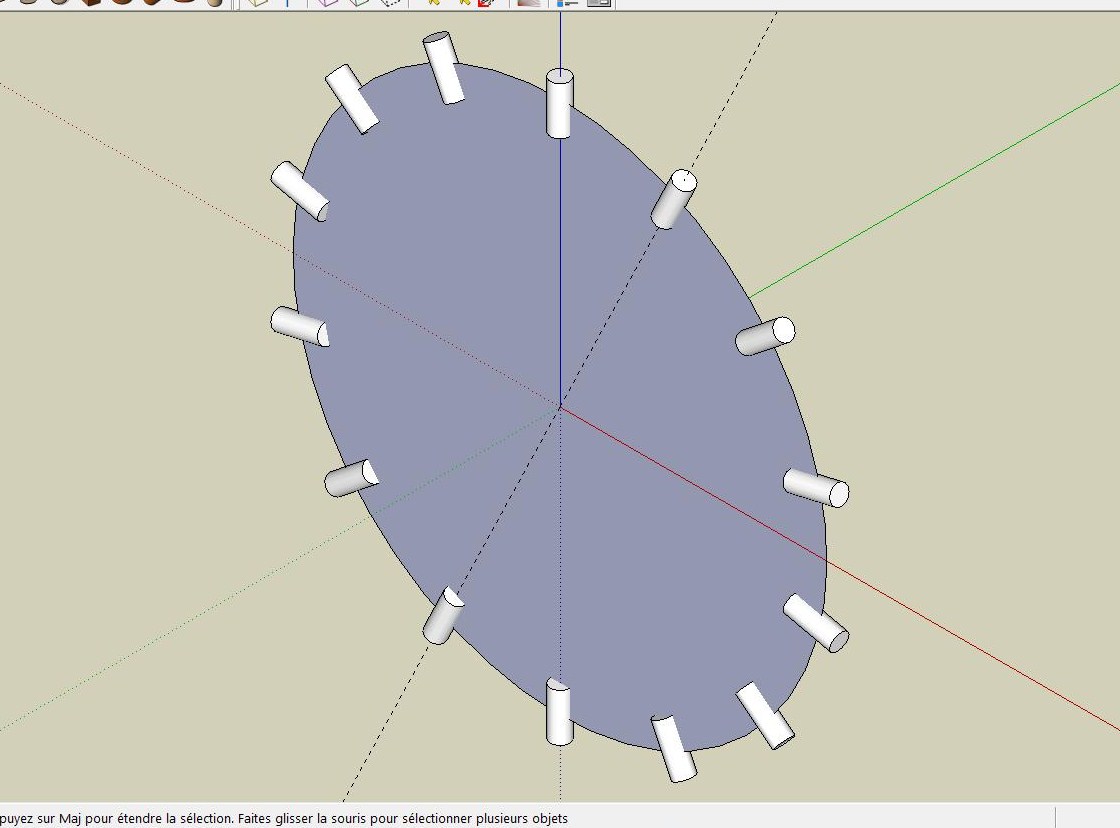
28 cm de rayon pour 28 trous. Attention, les trous sont répartis en 2 lignes séparées d'environ 3 mm, et les trous ne sont pas perpendiculaires à la jante mais parallèles aux rayons (ce n'est pas sorcier mais ça rajoute au plaisir !)

eddy

Salut, c'est sa que tu veux,
modl. jnt..jpg

Borishusser

Ben oui c'est ça, mais je ne comprends pas, tu sembles avoir utilisé le même principe que moi avec avec un cercle mieux segmenté. Et ça n'explique pas le problème de mon exemple

Borishusser

Bon ben SU a un problème avec le nb 14. En essayant avec un cercle à 28 segments je n'ai aucun problème...

pilou

Pouvez-vous poster en version 6 ou 7 (Save as V6)

eddy

Borishusser, j'ai fais avec la méthode du tuto que je t'ai fait:

V6

pilou

Et attention
un cercle de 14 côtés de rayon 1m fait 3.04 m2
un cercle de 28 côtés de rayon 1m fait 3.12 m2
Ce n'est pas négligeable suivant les utilisations!

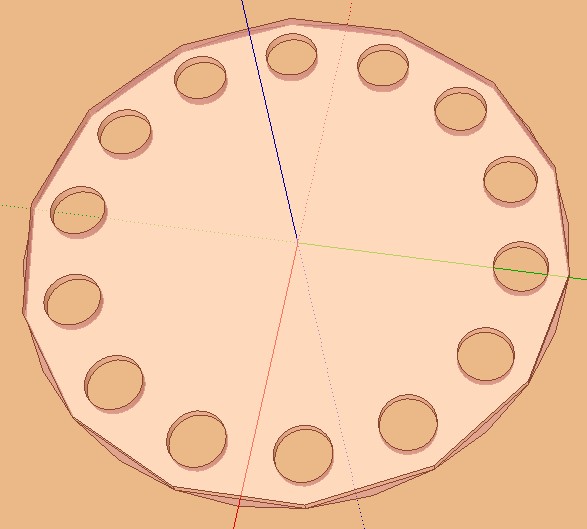
Sinon je ne vois pas de problème spécial avec 14
Il vaut mieux le dessiner en partant de l'origine
et "axer" le rayon principal sur un axe
en sachant que le quadrant suivant sera aligné sur le milieu
d'un segment (c'est la beauté relative des polygones)

Borishusser

Bonjour messieurs, et merci pour votre contribution.
Après quelques tests (parceque je n'allais pas non plus y passer trop de temps !)je constate qu'il n'y a pas de règle fénérale. Parfois SU le gère sans problème, parfois il fait un refus d'obstacle. Curieusement la "lourdeur" des objets ne rentre pas en compte. Enfin bon, les trous dans le moyeu sont finis, j'ai quelques trous à faire dans une jante maintenant (pour l'instant ma jante est beaucoup trop lourde et l'intersection des objets oublie des choses... il faut que je recommence...)

Merci encore, à bientôt